E-mail Alert
RSS
-
摘要
为了突出图像纹理细节的同时保留平滑区域，节省确定分数阶微分阶次的时间，提出了一种改进的自适应分数阶微分算子。首先将经典Tiansi模板分解为四个不同方向，分别与待处理像素点进行卷积，达到增强图像纹理细节的效果；其次针对Tiansi算子需通过多次实验确定最佳微分阶次的现状，结合图像的局部特征信息，构建了具有自适应能力的分数阶阶次模型，能够获得比原图像更丰富的细节信息。对多组不同场景图像的实验结果表明：构建的自适应分数阶微分算子有效地增强了图像的纹理细节，自适应分数阶微分算子的主观视觉效果和客观评价指标均优于原图像，其客观评价指标中的平均梯度、信息熵、对比度相比原图像平均提高190.3%、8.1%、18.3%；平均梯度、对比度相比Tiansi算子处理后的图像平均提高45.0%、9.6%。
Abstract
In order to highlight the texture details of the image while preserving the smooth region and saving the time to determine the fractional differential order, an improved adaptive fractional differential operator is proposed. Firstly, the classical Tiansi template is decomposed into four different directions, which are respectively convolved with the pixels to be processed to achieve the effect of enhancing the texture details of the image. Secondly, the current situation of the optimal differential order is determined by the experiment for the Tiansi operator. The local feature information of the image constructs a fractional order model with an adaptive ability, which can obtain more detailed information than the original image. The experimental results of multiple sets of different scene images show that the constructed adaptive fractional differential operators effectively enhance the texture details of the image. The subjective visual effects and objective evaluation indexes of the adaptive fractional differential operators are better than the original images. The average gradient, information entropy and contrast in the objective evaluation index are increased by 190.3%, 8.1%, and 18.3%, respectively. The average gradient and contrast are 45.0% and 9.6% higher than that of the Tiansi operator.
-
Key words:
- image enhancement /
- fractional differential /
- Tiansi operator /
- adaptive fractional
-
Overview
Overview: Image processing technology has become increasingly prominent in the fields of intelligent transportation and video surveillance. Visibility is relatively low in foggy weather and nighttime scenes, and images collected by equipment often have severe degradation and distortion. Therefore, it is especially important to study how to improve the quality of video images in bad weather. In the image enhancement processing, in order to improve the visual effect of the image, it is desirable that the high-frequency component of the image can be enhanced to highlight the texture information of the image while further smoothing the low-frequency component of the image. The linear transformation of the image has the advantage of smoothing the low-frequency components of the image, but such a method retains too little high-frequency components to achieve the desired effect. When the image is averaged or integrated, blurring occurs. In order to make the edge contour extending in any direction in the image clearer, the image can be inversely operated, such as differential operation. The first-order differential gradient operator and the second-order differential Laplacian operator have the advantage of not only enhancing high-frequency components of the image and highlighting texture information in the image, but also increasing the image noise. The traditional image enhancement processing can not solve the contradiction of removing image noise while enhancing the texture details of the image.
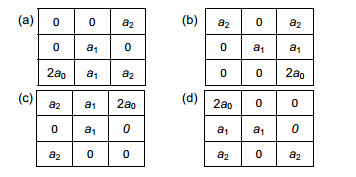
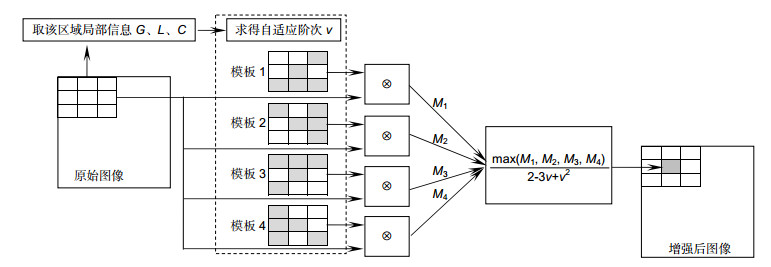
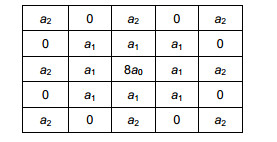
In recent years, fractional calculus has made breakthroughs in many fields. It has been found that fractional differential operators have the property of weak derivatives, and more and more people apply them to the field of image processing. In order to highlight the texture details of the image while preserving the smooth region and saving the time to determine the fractional differential order, an improved adaptive fractional differential operator is proposed. Firstly, the classical Tiansi template is decomposed into four different directions, which are respectively convolved with the pixels to be processed to achieve the effect of enhancing the texture details of the image. Secondly, the current situation of the optimal differential order is determined by the experiment for the Tiansi operator. The local feature information of the image constructs a fractional order model with an adaptive ability, which can obtain more detailed information than the original image. The experimental results of multiple sets of different scene images show that the constructed adaptive fractional differential operators effectively enhance the texture details of the image. The subjective visual effects and objective evaluation indexes of the adaptive fractional differential operators are better than the original images. The average gradient, information entropy and contrast in the objective evaluation index are increased by 190.3%, 8.1%, and 18.3%, respectively. The average gradient and contrast are 45.0% and 9.6% higher than that of the Tiansi operator.
-
-
图 2 按坐标轴分解为四个方向模板
Figure 2. Decomposition into four orientation templates by coordinate axes
图 3 Tiansi算子与改进算子处理后的对比图像
Figure 3. Contrast images processed by Tiansi operator and improved operator
图 4 自适应分数阶微分算子的具体处理步骤
Figure 4. Concrete processing steps of adaptive fractional differential operator
表 1 Lena图的客观评价
Table 1. Objective evaluations of Lena image
原图像 Laplacian Tiansi算子 文献[7]算子 改进算子 自适应算子 信息熵 5.4601 6.8303 7.6604 7.1410 7.5440 7.5471 平均梯度 6.0157 18.7322 12.2129 21.7388 20.1014 14.0116 图像对比度 43.8420 50.0691 47.1296 42.5253 51.9007 49.3702 SSIM \ 0.5260 0.7922 0.5569 0.5454 0.6703 
下载: 导出CSV
表 2 雾霾图像1的客观评价
Table 2. Objective evaluation of haze image 1
原图像 Laplacian Tiansi算子 文献[7]算子 改进算子 自适应算子 信息熵 7.3193 7.6280 7.6257 7.3430 7.6484 7.5170 平均梯度 3.6461 10.4439 7.7882 13.7948 12.6791 12.1317 图像对比度 41.6897 47.3064 45.0094 41.0306 50.0650 50.4051 SSIM \ 0.7546 0.8716 0.6219 0.6125 0.7571
下载: 导出CSV
表 3 雾霾图像2的客观评价
Table 3. Objective evaluation of haze image 2
原图像 Laplacian Tiansi算子 文献[7]算子 改进算子 自适应算子 信息熵 6.4407 6.5971 6.5237 6.4629 6.6755 6.6928 平均梯度 1.4535 4.7734 3.2798 6.9128 5.9013 5.4956 图像对比度 19.2248 19.5839 19.5757 16.0659 19.9807 19.4519 SSIM \ 0.8326 0.9244 0.7104 0.6749 0.8229
下载: 导出CSV
表 4 夜间图像1的客观评价
Table 4. Objective evaluation of night image 1
原图像 Laplacian Tiansi算子 文献[7]算子 改进算子 自适应算子 信息熵 7.0607 7.1267 7.0884 6.8329 7.1588 7.1336 平均梯度 1.6423 3.8517 2.9670 5.6480 4.8916 4.7185 图像对比度 37.0751 38.0947 37.7044 29.7156 38.8709 38.8115 SSIM \ 0.8822 0.9460 0.7510 0.7256 0.8498
下载: 导出CSV
表 5 夜间图像2的客观评价
Table 5. Objective evaluation of night image 2
原图像 Laplacian Tiansi算子 文献[7]算子 改进算子 自适应算子 信息熵 5.4228 5.5114 5.4795 5.2203 5.5392 5.4268 平均梯度 1.7520 3.5697 3.0279 4.5573 4.2556 4.1458 图像对比度 9.8958 11.4134 10.8980 11.1497 12.3368 13.2254 SSIM \ 0.9321 0.9654 0.8405 0.8282 0.9177
下载: 导出CSV
-
参考文献
[1] Svoboda T, Kybic J, Hlavac V. Image Processing, Analysis & and Machine Vision: A MATLAB Companion[M]. CL-Engineering, 2007: 712-717.
[2] 周尚波, 王李平, 尹学辉.分数阶偏微分方程在图像处理中的应用[J].计算机应用, 2017, 37(2): 546-552. http://d.old.wanfangdata.com.cn/Periodical/jsjyy201702043
Zhou S B, Wang L P, Yin X H. Applications of fractional partial differential equations in image processing[J]. Journal of Computer Applications, 2017, 37(2): 546-552. http://d.old.wanfangdata.com.cn/Periodical/jsjyy201702043
[3] Gao R, Gu C, Li X. Image zooming model based on fractional-order partial differential equation[J]. Journal of Discrete Mathematical Sciences and Cryptography, 2017, 20(1): 55-63. doi: 10.1080/09720529.2016.1178901
[4] 黄果, 陈庆利, 许黎, 等.可变阶次分数阶微分实现图像自适应增强[J].沈阳工业大学学报, 2012, 34(4): 446-454. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201203736574
Huang G, Chen Q L, Xu L, et al. Realization of adaptive image enhancement with variable fractional order differentials[J]. Journal of Shenyang University of Technology, 2012, 34(4): 446-454. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201203736574
[5] 蒲亦非.将分数阶微分演算引入数字图像处理[J].四川大学学报(工程科学版), 2007, 39(3): 124-132. doi: 10.3969/j.issn.1009-3087.2007.03.023
Pu Y F. Application of fractional differential approach to digital image processing[J]. Journal of Sichuan University (Engineering Science Edition), 2007, 39(3): 124-132. doi: 10.3969/j.issn.1009-3087.2007.03.023
[6] Pu Y F, Siarry P, Chatterjee A, et al. A fractional-order variational framework for retinex: fractional-order partial differential equation-based formulation for multi-scale nonlocal contrast enhancement with texture preserving[J]. IEEE Transactions on Image Processing, 2018, 27(3): 1214-1229. doi: 10.1109/TIP.2017.2779601
[7] 张绍阳, 解源源, 张鑫, 等.基于分数阶微分的模糊交通视频图像增强[J].光学精密工程, 2014, 22(3): 779-786. http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201403034
Zhang S Y, Xie Y Y, Zhang X, et al. Enhancement of fuzzy traffic video images based on fractional differential[J]. Optics and Precision Engineering, 2014, 22(3): 779-786. http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201403034
[8] 汪成亮, 兰利彬, 周尚波.自适应分数阶微分在图像纹理增强中的应用[J].重庆大学学报, 2011, 34(2): 32-37. http://d.old.wanfangdata.com.cn/Periodical/cqdxxb201102006
Wang C L, Lan L B, Zhou S B. Adaptive fractional differential and its application to image texture enhancement[J]. Journal of Chongqing University, 2011, 34(2): 32-37. http://d.old.wanfangdata.com.cn/Periodical/cqdxxb201102006
[9] 杨柱中, 周激流, 晏祥玉, 等.基于分数阶微分的图像增强[J].计算机辅助设计与图形学学报, 2008, 20(3): 343-348. http://d.old.wanfangdata.com.cn/Periodical/jsjfzsjytxxxb200803012
Yang Z Z, Zhou J L, Yu X Y, et al. Image enhancement based on fractional differentials[J]. Journal of Computer-Aided Design & Computer Graphics, 2008, 20(3): 343-348. http://d.old.wanfangdata.com.cn/Periodical/jsjfzsjytxxxb200803012
[10] 黄果, 许黎, 蒲亦非.分数阶微积分在图像处理中的研究综述[J].计算机应用研究, 2012, 29(2): 414-420, 426. doi: 10.3969/j.issn.1001-3695.2012.02.003
Huang G, Xu L, Pu Y F. Summary of research on image processing using fractional calculus[J]. Journal of Computer Applications, 2012, 29(2): 414-420, 426. doi: 10.3969/j.issn.1001-3695.2012.02.003
[11] Ma Q T, Dong F F, Kong D X. A fractional differential fidelity-based PDE model for image denoising[J]. Machine Vision and Applications, 2017, 28(5-6): 635-647. doi: 10.1007/s00138-017-0857-z
[12] Pu Y F, Wang W X, Zhou J L, et al. Fractional differential approach to detecting textural features of digital image and its fractional differential filter implementation[J]. Science in China Series F: Information Sciences, 2008, 51(9): 1319-1339. doi: 10.1007/s11432-008-0098-x
[13] 余萍, 郝成成.基于分数阶微分和多尺度Retinex联合的雾霭图像增强算法[J].激光与光电子学进展, 2018, 55(1): 272-277. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgygdzxjz201801033
Yu P, Hao C C. Foggy image enhancement by combined fractional differential and multi-scale retinex[J]. Advances in Laser and Optoelectronics, 2018, 55(1): 272-277. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jgygdzxjz201801033
[14] Pu Y F. Fractional-order euler-Lagrange equation for fractional-order variational method: A necessary condition for fractional-order fixed boundary optimization problems in signal processing and image processing[J]. IEEE Access, 2016, 4: 10110-10135. doi: 10.1109/ACCESS.2016.2636159
[15] 吴瑞芳, 宣士斌, 荆奇.基于局部特征的分数阶微分图像增强方法[J].计算机工程与应用, 2014, 50(3): 160-164. doi: 10.3778/j.issn.1002-8331.1203-0619
Wu R F, Xuan S B, Jing Q. Fractional differential image enhancement algorithm based on local feature[J]. Computer Engineering and Applications, 2014, 50(3): 160-164. doi: 10.3778/j.issn.1002-8331.1203-0619
[16] Wang Z, Bovik A C, Sheikh H R, et al. Image quality assessment: from error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. doi: 10.1109/TIP.2003.819861
-
访问统计
点击扫一扫
图(9)
表(5)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
