E-mail Alert
RSS
-
摘要:
光纤陀螺(FOG)温度漂移数据常常淹没在各种噪声背景中，直接补偿建模漂移信号十分困难，为了更好地消除混杂在光纤陀螺温漂数据中的噪声，提出了一种经验模态分解(EMD)和提升小波变换(LWT)相结合的EMD-LWT滤波方法对光纤陀螺输出信号进行预处理。首先对光纤陀螺含噪信号进行EMD分解，根据信息熵值判断本征模态函数(IMF)的噪声项和混合模态项，然后对噪声项进行LWT去噪，混合模态项进行小波分析去噪。对某干涉型FOG进行静态测试获得陀螺漂移数据，本文提出方法与小波变换和提升小波变换滤波方法进行了对比分析。实测数据计算结果表明，本文提出的EMD-LWT滤波算法具有最好的滤波效果，经处理后重构信号的均方根误差(RMSE)下降了63%，有效地滤除了FOG输出中的噪声。
Abstract:Fiber optic gyroscope (FOG) drift data is often submerged in various noises backgrounds. It is very difficult to compensate for modeling drift signals directly. In order to better eliminate the noise mixed in the FOG temperature drift data, a hybrid EMD-LWT filtering algorithm based on empirical mode decomposition (EMD) and lifting wavelet transform (LWT) threshold denoising was proposed for gyro signals preprocessing. Firstly, the noise signal of fiber optic gyro is decomposed by EMD, and the noise term and the mixed modal term of the intrinsic mode functions (IMF) are judged according to the information entropy. Then the noise term is de-noised by LWT and the mixed modal term is denoised by wavelet transform (WT). A static test was performed on an interferential FOG to verify the effectiveness of the algorithm and compared with WT and LWT. The experimental results show that the proposed EMD-LWT filtering algorithm has better filtering effect. After processing, the root mean square error (RMSE) of the reconstructed signal is reduced by 63%, which effectively removes the noise in the FOG output.
-
Key words:
- fiber optic gyroscope /
- wavelet analysis /
- EMD-LWT /
- filtering
-
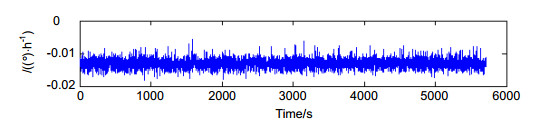
Overview: Fiber optic gyro (FOG) is an inertial sensor based on the Sagnac effect. It has the advantages of high reliability, high measurement accuracy, and ease of integration. It has become an ideal device for inertial navigation systems. The collected FOG drift data is affected by many factors such as the light source, fiber bending, and ambient temperature, making it often submerged in the noise and leading to difficulties in direct modeling compensation. In order to establish an accurate error compensation model, data preprocessing is demanded to output data on the gyro.
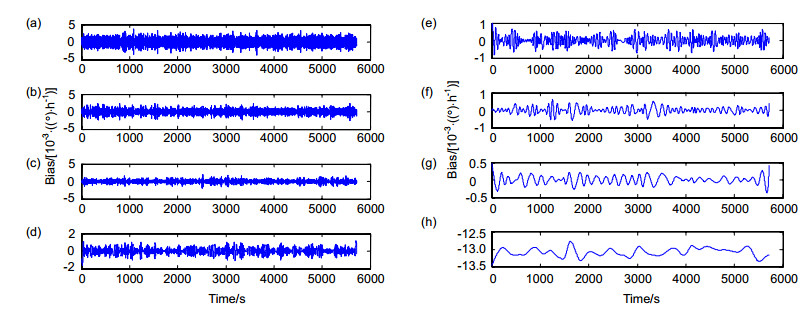
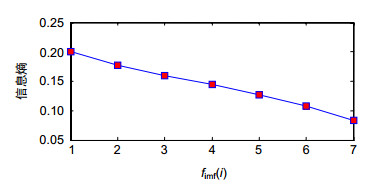
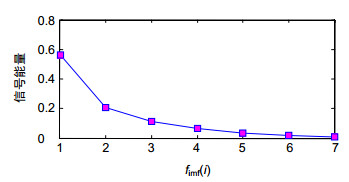
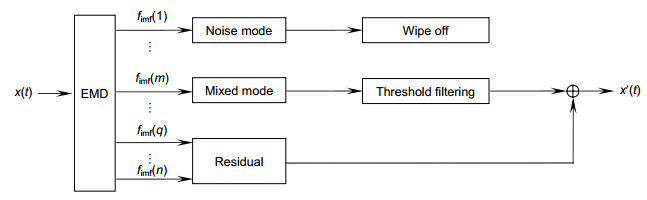
In this paper, a hybrid EMD-LWT filtering algorithm based on empirical mode decomposition (EMD) and lifting wavelet transform (LWT) threshold denoising is proposed to preprocess gyro signals. Firstly, the steps of empirical mode decomposition are introduced. After the signal is decomposed by EMD, a finite number of high-to-low frequency intrinsic mode functions (IMFs) are obtained. The low order part represents the high frequency part of the signal, which usually contains a sharp part or noise; An IMF with a large order corresponds to the low-frequency part of the signal, and it is generally considered that the noise in the low-frequency component has little effect. It is decomposed into noise-dominated IMF sets, where noise and effective information coexist and a signal low-frequency trend. The threshold filtering method based on EMD is a process to select and threshold three types of IMF sets. The information entropy and the energy of the signal serve as a measurement of the complexity of the signal and determine the boundaries of the noise component and the mixed modal component.
Considering that the traditional EMD time-scale filtering algorithm simply removes one or more IMF components to achieve filtering, resulting in the useful signals along the corresponding components being deleted together. It will lead to severe signal distortion. The lifting wavelet analysis is introduced into the EMD method, and the high-frequency IMF component is subjected to the narrowband re-decomposition of the lifting wavelet to improve the resolution of the high-frequency component; considering the noise decomposition after being distributed on each IMF component, combined with the characteristics of wavelet threshold denoising. All IMF components are subjected to wavelet threshold denoising.
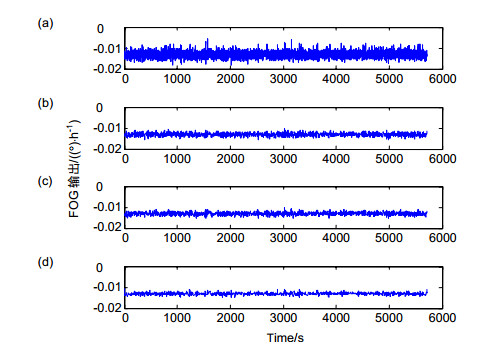
A static FOG data was collected as a test signal for verifying the effectiveness of the algorithm. The hybrid EMD-LWT was compared with the wavelet transform (WT) and the lifting wavelet transform (LWT) threshold filtering methods. The simulation results show that the root mean squared error (RMSE) of the signal is reduced by 63% through the EMD-LWT filtering algorithm and the denoising effect is obvious.
-
-
图 2 小波提升方案的分解和重构过程。(a)提升分解; (b)提升重构
Figure 2. Decomposition and reconstruction process of wavelet lifting scheme. (a) Lifting decomposition; (b) Lifting reconstruction
图 5 FOG温度漂移EMD分解图。(a) fimf(1); (b) fimf(2); (c) fimf(3); (d) fimf(4); (e) fimf(5); (f) fimf(6); (g) fimf(7); (h) Trend
Figure 5. EMD decomposition of FOG temperature drift. (a) fimf(1); (b) fimf(2); (c) fimf(3); (d) fimf(4); (e) fimf(5); (f) fimf(6); (g) fimf(7); (h) Trend
表 1 四种滤波方法的性能对比
Table 1. Performance comparison of the four filtering methods
指标 原信号 DB4小波消噪 Haar提升小波 DB4提升小波 EMD-LWT RMES/[(°)·h-1] 1.374e-3 6.720e-4 6.622e-4 5.467e-4 5.116e-4 SSE/[(°)·h-1]2 1.080e-2 2.590e-3 2.507e-3 1.709e-3 1.497e-3 R/[(°)·h-1] 1.65e-2 5.577e-3 4.941e-3 4.706e-3 4.323e-3 
下载: 导出CSV
-
[1] 李绪友, 刘攀, 光星星, 等.保偏光纤陀螺横向磁场误差的温度依赖性[J].光学学报, 2018, 38(1): 0106006. doi: 10.3788/aos201838.0106006
Li X Y, Liu P, Guang X X, et al. Temperature dependence of transverse magnetic error in a polarization maintaining fiber optic gyroscope[J]. Acta Optica Sinica, 2018, 38(1): 0106006. doi: 10.3788/aos201838.0106006
[2] 律新伟, 武俊勇, 孙丽艳.单模光纤环热应力双折射仿真分析[J].导航与控制, 2015, 14(3): 94–97. doi: 10.3969/j.issn.1674-5558.2015.03.016
Lv X W, Wu J Y, Sun L Y. Thermal stress birefringence simulation of single mode optic fiber loop[J]. Navigation and Control, 2015, 14(3): 94–97. doi: 10.3969/j.issn.1674-5558.2015.03.016
[3] 陈一平, 梁璀, 张登伟, 等.光纤陀螺磁温耦合效应[J].光子学报, 2018, 47(5): 0506005. doi: 10.3788/gzxb20184705.0506005
Chen Y P, Liang C, Zheng D W, et al. Magnetic-temperature coupling effect of a fiber optic gyroscope[J]. Acta Photonica Sinica, 2018, 47(5): 0506005. doi: 10.3788/gzxb20184705.0506005
[4] Dang S W, Tian W F, Qian F. EMD- and LWT-based stochastic noise eliminating method for fiber optic gyro[J]. Measurement, 2011, 44(10): 2190–2193. doi: 10.1016/j.measurement.2011.07.016
[5] Li Z H, Meng Z, Liu T G, et al. A novel method for determining and improving the quality of a quadrupolar fiber gyro coil under temperature variations[J]. Optics Express, 2013, 21(2): 2521–2530. doi: 10.1364/OE.21.002521
[6] 吕品, 刘建业, 赖际舟, 等.光纤陀螺实时小波去噪中的阈值选取[J].弹箭与制导学报, 2009, 29(1): 18–22. doi: 10.3969/j.issn.1673-9728.2009.01.006
Lv P, Liu J Y, Lai J Z, et al. Research on threshold algorithm in real-time wavelet de-noising of FOG[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2009, 29(1): 18–22. doi: 10.3969/j.issn.1673-9728.2009.01.006
[7] 王庆贺.基于小波去噪与DRNN的光纤陀螺随机误差建模研究[J].航空兵器, 2015(4): 16–20. doi: 10.3969/j.issn.1673-5048.2015.04.004
Wang Q H. Research of gyro random error modeling based on the wavelet and DRNN[J]. Aero Weaponry, 2015(4): 16–20. doi: 10.3969/j.issn.1673-5048.2015.04.004
[8] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903–995. doi: 10.1098/rspa.1998.0193
[9] Komaty A, Boudraa A O, Augier B, et al. EMD-based filtering using similarity measure between probability density functions of IMFs[J]. IEEE Transactions on Instrumentation and Measurement, 2014, 63(1): 27–34. doi: 10.1109/TIM.2013.2275243
[10] 席旭刚, 武昊, 罗志增.基于EMD自相关的表面肌电信号消噪方法[J].仪器仪表学报, 2014, 35(11): 2494–2500. doi: 10.3969/j.issn.0254-3087.2014.11.011
Xi X G, Wu H, Luo Z Z. De-noising method of the sEMG based on EMD autocorrelation[J]. Chinese Journal of Scientific Instrument, 2014, 35(11): 2494–2500. doi: 10.3969/j.issn.0254-3087.2014.11.011
[11] 刘海江, 刘世高, 李敏.换挡加速度信号的EMD和小波阈值降噪方法[J].噪声与振动控制, 2018, 38(2): 198–203. doi: 10.3969/j.issn.1006-1355.2018.02.037
Liu H J, Liu S G, Li M. EMD and wavelet threshold denoising method of gear-shift acceleration signals[J]. Noise and Vibration Control, 2018, 38(2): 198–203. doi: 10.3969/j.issn.1006-1355.2018.02.037
[12] Bekiros S, Nguyen D K, Junior L S, et al. Information diffusion, cluster formation and entropy-based network dynamics in equity and commodity markets[J]. European Journal of Operational Research, 2017, 256(3): 945–961. doi: 10.1016/j.ejor.2016.06.052
[13] Belazi A, El-Latif A A A, Diaconu A V, et al. Chaos-based partial image encryption scheme based on linear fractional and lifting wavelet transforms[J]. Optics and Lasers in Engineering, 2017, 88: 37–50. doi: 10.1016/j.optlaseng.2016.07.010
[14] Chen X Y, Shen C. Study on temperature error processing technique for fiber optic gyroscope[J]. Optik, 2013, 124(9): 784–792. doi: 10.1016/j.ijleo.2012.02.008
[15] 杨秀芳, 张伟, 杨宇祥.基于提升小波变换的雷达生命信号去噪技术[J].光学学报, 2014, 34(3): 0328003. doi: 10.3788/AOS201434.0328003
Yang X F, Zhang W, Yang Y X. Denoising technology of radar life signal based on lifting wavelet transform[J]. Acta Optica Sinica, 2014, 34(03): 0328003. doi: 10.3788/AOS201434.0328003
[16] Li M X, Mao H P, Zhang Y C, et al. Fusion algorithm for multi–sensor images based on PCA and lifting wavelet transformation[J]. New Zealand Journal of Agricultural Research, 2007, 50(5): 667–671. doi: 10.1080/00288230709510336
-
点击扫一扫
图(8)
表(1)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
