E-mail Alert
RSS
-
摘要:
牛眼结构是一种典型的纳米光学结构。本文设计了一种带有同轴纳米柱的牛眼结构，利用时域有限差分法(FDTD)研究了该结构的增强透射效应。研究发现，柱的半径和高度对透射特性具有显著的影响，恰当选择柱的半径和高度会得到最大的透射强度。另外，牛眼结构对环境折射率有较高的灵敏度。理论分析表明，该种结构的透射增强效应是由局域表面等离激元与表面极化等离激元相互作用产生。这为纳米光学元件的研发与应用提供一个新的思路。
Abstract:The bullseye structure is a classic nano-optical structure. This article designs a new bullseye structure with coaxial nano-pillars. We used the time-domain finite difference method (FDTD) to study the EOT of the structure. Studies show that the radius and height of the column have a significant impact on the transmission characteristics. The proper choice of the radius and height of the column will support the maximum transmission intensity. In addition, the bullseye structure has a higher sensitivity to the environmental refractive index. Theoretical analyses show that the enhancement transmission effect of the structure is caused by the interaction between the local surface plasmon and the surface plasmon polarization. This provides a new idea for the development and application of nano-photonic components.
-
Key words:
- surface plasmon /
- EOT /
- bullseye structure /
- finite difference time domain method
-
Overview: In 1998, the Ebbesen team reported the phenomenon of extraordinary optical transmission in arrays of subwavelength hole on metal substrate. Since then, people have conducted extensive research on the mechanism of EOT and proposed several theoretical models. Ebbesen, Ghaemi et al. proposed surface plasmon excitation and Wood extraordinary effects. In 2004, Koerkamp et al. studied the influence of the aspect ratio of the rectangular aperture on the transmission peak and the central wavelength. They believed that the coupling between local waveguide resonance and plasmon resonance led to EOT. Similar models also have compound diffraction evanescent wave mode proposed by Lezec and Thio et al. At present, people mainly use square holes, round holes, triangular holes, wedge-shaped slits, and groove arrays to study EOT. The bullseye structure is a kind of round-hole structure. It is a single-hole structure surrounded by periodic surface corrugation proposed by Thio in 2002. Due to its circular symmetry, it can make Huygens waves better matches the plasmon mode under random polarized light, so it has a higher transmission coefficient than the square-hole structure and the groove array structure.
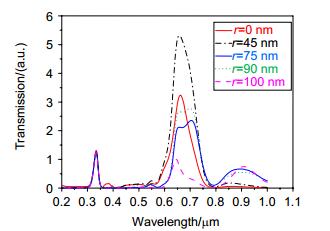
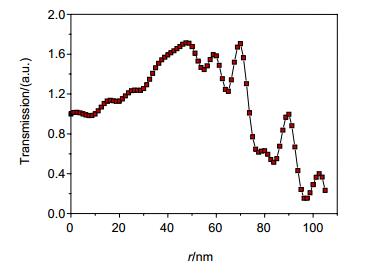
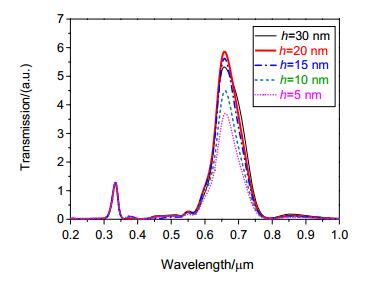
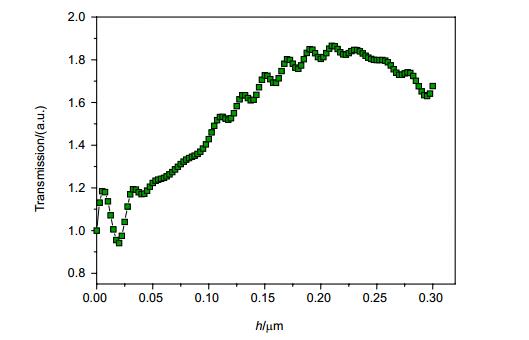
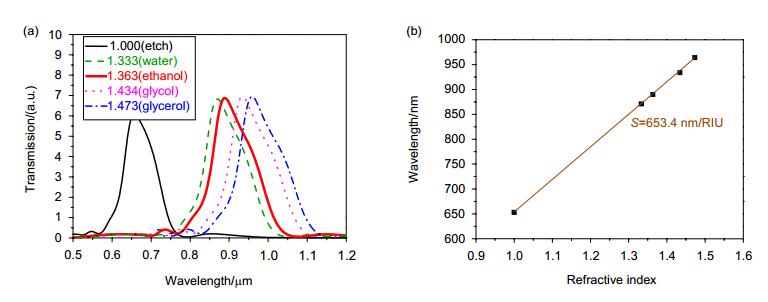
We designed a bullseye structure with coaxial nano-pillars and used the finite-difference time-domain method to simulate the transmission characteristics of proposed new structure. The specific simulation tool we used is FDTD Solution. We studied the influence of the radius and height of the nano-column on the transmission. The results show that changing the radius and height of the column can significantly change the peak and resonance wavelength of the main transmission peak. When the nano-column has a radius of 46 nm and a height of 20 nm, the bullseye structure obtains the maximum transmission intensity, whose the main transmission peak increases by about 90% compared to the bullseye structure without filling. In addition, the main transmission peak wavelength of the structure changes approximately linearly with the ambient refractive index, and the refractive index sensitivity can reach 653.4 nm/RIU. Theoretical analyses show that the physical mechanism of the effect of nano-columns on the transmission characteristics of bullseye structures is that under the excitation of incident light, the LSP polarized by the nano-columns couples with the SPP and LSP existing in the structure, resulting in a change in resonance position and intensity, further leading to frequency shifts and peak changes. By changing the geometry of the nano-pillars, the transmitted light intensity of the bullseye structure can be controlled. In addition, because the structure has a high sensitivity to environmental refractive index, it has potential applications in the field of refractive index sensors.
-
-
图 1 纳米柱牛眼结构的模型。(a) X-Z面截面图；(b) X-Y面截面图
Figure 1. Model of the bullseye structure with nano-column.(a) X-Z cross section; (b) X-Y cross section
图 2 纳米柱半径不同的牛眼结构的透射率
Figure 2. Transmittance of the bullseye structures with different-radii nano-columns
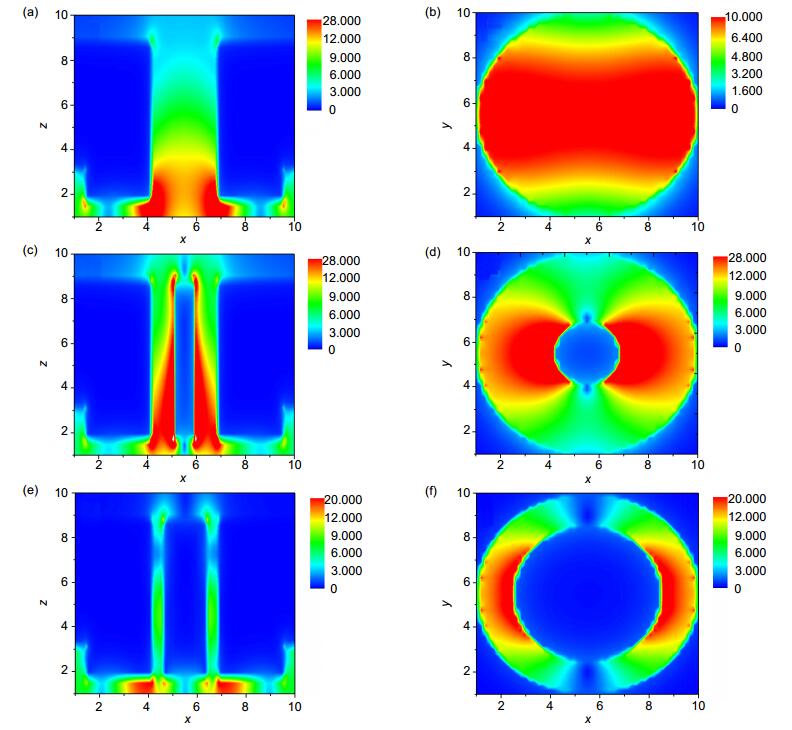
图 3 纳米柱半径不同时，牛眼结构在共振波长下的电场分布。(a) XOZ电场(λ=660 nm, r=0 nm)；(b) XOY电场(λ=660 nm, r=0 nm)；(c) XOZ电场(λ=653 nm, r=45 nm); (d) XOY电场(λ=653 nm, r=45 nm); (e) XOZ电场(λ=647 nm, r=100 nm); (f) XOY电场(λ=647 nm, r=100 nm)
Figure 3. Electric field distributions of the bullseye structures with different-radii nano-columns at the resonance wavelengths.(a) XOZ electric field(λ=660 nm, r=0 nm); (b) XOY electric field(λ=660 nm, r=0 nm); (c) XOZ electric field(λ=653 nm, r=45 nm); (d) XOY electric field(λ=653 nm, r=45 nm); (e) XOZ electric field(λ=647 nm, r=100 nm); (f) XOY electric field (λ=647 nm, r=100 nm)
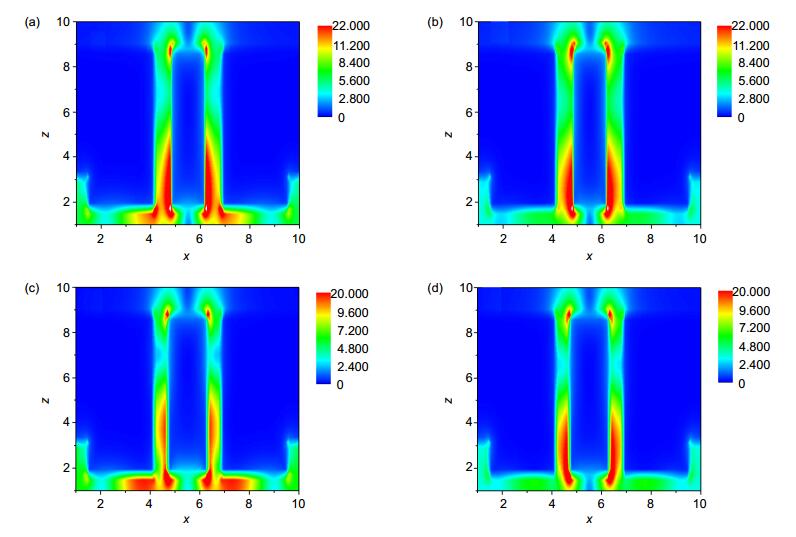
图 4 纳米柱的半径不同时，牛眼结构在共振波长下的电场分布。(a) XOZ电场(λ=654 nm, r=75 nm)；(b) XOZ电场(λ=714 nm, r=75 nm)；(c) XOZ电场(λ=654 nm, r=90 nm)；(d) XOZ电场(λ=714 nm, r=90 nm)
Figure 4. Electric field distributions of the bullseye structures with different-radii nano-columns at the resonant wavelengths.(a) XOZ electric field(λ=654 nm, r=75 nm); (b) XOZ electric field(λ=714 nm, r=75 nm); (c) XOZ electric field(λ=654 nm, r=90 nm); (d) XOZ electric field(λ=714 nm, r=90 nm)
图 5 r=75 nm时电场分布的两种模式。(a)模式1；(b)模式2
Figure 5. Two modes of electric field distribution of the bullseye structure with 75 nm nano-column.(a) Mode 1; (b) Mode 2
图 6 纳米柱不同半径时，牛眼结构的透射电场峰值
Figure 6. Transmitted electric field peaks of bullseye structures with different-radii nano-columns
图 7 填充不同高度纳米柱时牛眼结构的透射率
Figure 7. Transmissions of bullseye structures with differentheight nano-columns
图 8 填充不同高度的纳米柱时，牛眼结构在共振波长下的电场分布。(a) XOZ静态电场(λ=657 nm, h=20 nm)；(b) XOY静态电场(λ=657 nm, h=20 nm)；(c) XOZ静态电场(λ=659 nm, h=10 nm)；(d) XOY静态电场(λ=659 nm, h=10 nm)
Figure 8. Electric field distributions of the bullseye structures with different-heights nano-columns at the resonance wavelengths.(a) XOZ electric field (λ=657 nm, h=20 nm); (b) XOY electric field (λ=657 nm, h=20 nm); (c) XOZ electric field (λ=659 nm, h=10 nm); (d) XOY electric field (λ=659 nm, h=10 nm)
图 9 透射电场强度在不同高度纳米柱时的透射曲线
Figure 9. Transmitted electric field peaks of bullseye structures with different-heights nano-columns
-
[1] Ebbesen T W, Lezec H J, Ghaemi H F, et al. Extraordinary optical transmission through sub-wavelength hole arrays[J]. Nature, 1998, 391(6668): 667–669. doi: 10.1038/35570
[2] Ghaemi H F, Thio T, Grupp D E, et al. Surface plasmons en- hance optical transmission through subwavelength holes[J]. Physical Review B, 1998, 58(11): 6779–6782. doi: 10.1103/PhysRevB.58.6779
[3] Martín-Moreno L, García-Vidal F J, Lezec H J, et al. Theory of extraordinary optical transmission through subwavelength hole arrays[J]. Physical Review Letters, 2001, 86(6): 1114–1147. doi: 10.1103/PhysRevLett.86.1114
[4] Popov E, Nevière M, Enoch S, et al. Theory of light transmission through subwavelength periodic hole arrays[J]. Physical Review B, 2000, 62(23): 16100–16108. doi: 10.1103/PhysRevB.62.16100
[5] Barnes W L, Murray W A, Dintinger J, et al. Surface plasmon polaritons and their role in the enhanced transmission of light through periodic arrays of subwavelength holes in a metal film[J]. Physical Review Letters, 2004, 92(10): 107401. doi: 10.1103/PhysRevLett.92.107401
[6] Koerkamp K J K, Enoch S, Segerink F B, et al. Strong influence of hole shape on extraordinary transmission through periodic arrays of subwavelength holes[J]. Physical Review Letters, 2004, 92(18): 183901. doi: 10.1103/PhysRevLett.92.183901
[7] Ruan Z C, Qiu M. Enhanced transmission through periodic arrays of subwavelength holes: the role of localized waveguide resonances[J]. Physical Review Letters, 2006, 96(23): 233901. doi: 10.1103/PhysRevLett.96.233901
[8] Najiminaini M, Vasefi F, Kaminska B, et al. A three-dimensional plasmonic nanostructure with extraordinary optical transmission[J]. Plasmonics, 2013, 8(2): 217–224. doi: 10.1007/s11468-012-9378-9
[9] Lezec H J, Thio T. Diffracted evanescent wave model for enhanced and suppressed optical transmission through subwavelength hole arrays[J]. Optics Express, 2004, 12(16): 3629–3651. doi: 10.1364/OPEX.12.003629
[10] Gay G, Alloschery O, de Lesegno B V, et al. The optical response of nanostructured surfaces and the composite diffracted evanescent wave model[J]. Nature Physics, 2006, 2(4): 262–267. doi: 10.1038/nphys264
[11] Degiron A, Lezec H J, Barnes W L, et al. Effects of hole depth on enhanced light transmission through subwavelength hole arrays[J]. Applied Physics Letters, 2002, 81(23): 4327–4329. doi: 10.1063/1.1526162
[12] Wang J, Zhou W, Li E P. Enhancing the light transmission of plasmonic metamaterials through polygonal aperture arrays[J]. Optics Express, 2009, 17(22): 20349–20354. doi: 10.1364/OE.17.020349
[13] Matteo J A, Hesselink L. Fractal extensions of near-field aperture shapes for enhanced transmission and resolution[J]. Optics Express, 2005, 13(2): 636–647. doi: 10.1364/OPEX.13.000636
[14] 秦艳, 曹威, 张中月.内嵌矩形腔楔形金属狭缝的增强透射[J].物理学报, 2013, 62(12): 127302. doi: 10.7498/aps.62.127302
Qin Y, Cao W, Zhang Z Y. Enhanced optical transmission through metallic slits embedded with rectangular cavities?[J]. Acta Physica Sinica, 2013, 62(12): 127302. doi: 10.7498/aps.62.127302
[15] 肖功利, 郑龙, 王宏庆, 等.内嵌镜像对称矩形腔楔形金属狭缝阵列的宽带增强透射[J].半导体光电, 2016, 37(4): 505–509, 514. http://d.old.wanfangdata.com.cn/Periodical/bdtgd201604011
Xiao G L, Zheng L, Wang H Q, et al. Broadband enhanced transmission through wedge-shape metallic slits array embedded with mirror symmetric rectangular cavities[J]. Semiconductor Optoelectronics, 2016, 37(4): 505–509, 514. http://d.old.wanfangdata.com.cn/Periodical/bdtgd201604011
[16] Hibbins A P, Sambles J R, Lawrence C R. Gratingless enhanced microwave transmission through a subwavelength aperture in a thick metal plate[J]. Applied Physics Letters, 2002, 81(24): 4661–4663. doi: 10.1063/1.1527704
[17] Kim S, Jang M S, Brar V W, et al. Electronically tunable extraordinary optical transmission in graphene plasmonic ribbons coupled to subwavelength metallic slit arrays[J]. Nature Communications, 2016, 7: 12323. doi: 10.1038/ncomms12323
[18] Wei F F, Wang H Y, Zhou Y S. Effects of interplay between metal subwavelength slits on extraordinary optical transmission[J]. Chinese Physics B, 2013, 22(2): 024201. doi: 10.1088/1674-1056/22/2/024201
[19] Dmitriev V, Paix o F, Kawakatsu M. Enhancement of Faraday and Kerr rotations in three-layer heterostructure with extraordinary optical transmission effect[J]. Optics Letters, 2013, 38(7): 1052–1054. doi: 10.1364/OL.38.001052
[20] 岳宏卫, 邓进丽, 朱智勇, 等.纳米狭缝耦合金属圆-矩形复合孔阵列结构增强光透射[J].光电工程, 2016, 43(8): 7–12. doi: 10.3969/j.issn.1003-501X.2016.08.002
Yue H W, Deng J L, Zhu Z Y, et al. Extraordinary optic transmission of metallic circle-rectangular compound hole array with nano-slit coupling[J]. Opto-Electronic Engineering, 2016, 43(8): 7–12. doi: 10.3969/j.issn.1003-501X.2016.08.002
[21] Thio T, Pellerin K M, Linke R A, et al. Enhanced light transmission through a single subwavelength aperture[J]. Optics Letters, 2001, 26(24): 1972–1974. doi: 10.1364/OL.26.001972
[22] Lezec H J, Degiron A, Devaux E, et al. Beaming light from a subwavelength aperture[J]. Science, 2002, 297(5582): 820–822. doi: 10.1126/science.1071895
[23] Jimba Y, Takano K, Hangyo M, et al. Extraordinary optical transmission through incommensurate metal hole arrays in the terahertz region[J]. Journal of the Optical Society of America B, 2013, 30(9): 2476–2482. doi: 10.1364/JOSAB.30.002476
[24] 潘旭, 李民权, 汪善栋, 等.基于开口谐振环的多频太赫兹透射特性研究[J].量子电子学报, 2017, 34(3): 333–338. http://d.old.wanfangdata.com.cn/Periodical/lzdzxb201703010
Pan X, Li M Q, Wang S D, et al. Transmission characteristics of multi-frequency terahertz based on split ring resonators[J]. Chinese Journal of Quantum Electronics, 2017, 34(3): 333–338. http://d.old.wanfangdata.com.cn/Periodical/lzdzxb201703010
[25] Beaskoetxea U, Beruete M, Zehar M, et al. Flat THz leaky wave antennas: analysis and experimental results[C]//Proceedings of the 2014 8th International Congress on Advanced Electromagnetic Materials in Microwaves and Optics, Lyngby, Denmark, 2014: 55–57.
[26] Heggie T J, Naylor D A, Gom B G, et al. Enhanced transmission and beam confinement using bullseye plasmonic lenses at THz frequencies[J]. Proceedings of SPIE, 2014, 8985: 89851G. doi: 10.1117/12.2040335
[27] Palik E D. Handbook of Optical Constants of Solids[K]. London: Academic, 1985: 189.
[28] Karabchevsky A, Krasnykov O, Abdulhalim I, et al. Metal grating on a substrate nanostructure for sensor applications[J]. Photonics and Nanostructures - Fundamentals and Applications, 2009, 7(4): 170–175. doi: 10.1016/j.photonics.2009.05.001
[29] Lee M H, Gao H W, Odom T W. Refractive index sensing using quasi one-dimensional nanoslit arrays[J]. Nano Letters, 2009, 9(7): 2584–2588. doi: 10.1021/nl900773m
-
下载:
点击扫一扫
图(10)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
