E-mail Alert
RSS
-
摘要
图像超分辨率重建是利用单幅或多幅降质的低分辨率图像重建得到高分辨率图像，以提高图像的视觉效果并获得更多可用的信息。本文提出结合图像特征聚类和协同表示的超分辨率重建方法。在训练阶段根据图像的特征信息对图像样本进行聚类并利用图像特征的差异性训练不同的字典，克服了传统训练单个字典方法对图像特征表示不足的缺点。而且利用协同表示方法求得不同聚类的高、低分辨率图像样本之间的映射矩阵，提高了图像重建速度。实验表明，本文方法与其他方法相比，不仅提高了重建图像的PSNR和SSIM指标，而且改善了视觉效果。
Abstract
Image super-resolution (SR) refers to the reconstruction of a high-resolution (HR) image from single or multiple observed degraded low-resolution (LR) images for the purpose of improving image's visual effects and getting more available information. We propose an image super-resolution algorithm based on collaborative representation and clustering in this paper. In the training stage, the image samples are clustered according to the image features and multiple dictionaries are trained by using the differences of image features, which overcomes the shortcoming of lack of expressiveness of traditional single-dictionary training methods. Moreover, projection matrices between different HR and LR image clustering are computed via collaborative representation, which accelerate the speed of image reconstruction. Experiments demonstrate that compared with other methods, the proposed method not only enhanced PSNR and SSIM metrics for reconstructed images but also improved image's visual effects.
-
Key words:
- image super-resolution /
- clustering /
- collaborative representation /
- projection matrices
-
Overview
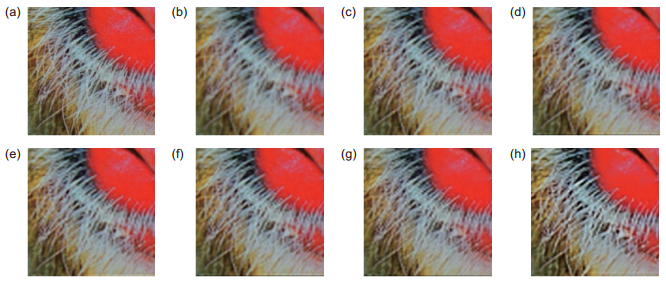
Overview: Image super-resolution (SR), as an important branch of digital image processing and computer vision, has been widely used in video surveillance, medical imaging and remote sensing image processing in these years. The single-image super-resolution (SISR) is currently a very active area of SR research and we focus on it in this paper. The SISR refers to the reconstruction of a high-resolution (HR) image from an observed degraded low-resolution (LR) image. In this paper, we propose a novel single image super-resolution algorithm by combining clustering and collaborative representation. In the training stage of our method, image patches with similar characteristics are clustered into one sub-class by using k-means clustering algorithm firstly, and then use clustered image patches to learn LR dictionary for each sub-class through K-SVD method. The HR dictionary is computed by using the sparse representation theory which assume that the LR and HR image patches have the same sparse coefficient according to corresponding LR and HR dictionaries. Finally, we compute the projection matrix for each clustered dictionary atom based on the CR with l2-norm regularization, which map LR features onto corresponding HR features. In the reconstruction process, for each input LR patch we first find the nearest LR cluster center and then obtain the projection matrix via closet dictionary atom in the corresponding LR dictionary. The HR patch can be estimated by multiplying input LR patch and the projection matrix at last. In conclusion, more expressiveness dictionaries and more effective projection matrices are obtained via our method.Experimental results demonstrate that our proposed algorithm is both quantitatively and qualitatively superior to other classic image SR algorithms. The visual results of HR images show that our proposed algorithm reconstructs more fine details along the dominant edges and suppresses the unexpected artifacts comparing with other methods.
-
-
图 2 k-means聚类后的两类图像块。(a)类别一；(b)类别二
Figure 2. Two categories obtained by k-means clustering. (a) Category one; (b) Category two
图 3 测试集。(a)狒狒；(b)芭芭拉；(c)桥；(d)海警；(e)漫画；(f)脸；(g)花；(h)工长；(i)莱娜图；(j)男人；(k)蝴蝶；(l)胡椒；(m)幻灯片；(n)斑马
Figure 3. Test image. (a) Baboon; (b) Barbara; (c) Bridge; (d) Coastguard; (e) Comic; (f) Face; (g) Flowers; (h) Foreman; (i) Lenna; (j) Man; (k) Monarch; (l) Pepper; (m) PPT; (n) Zebra
图 4 图片Baboon超分辨率重建效果图。(a)原图；(b) Bicubic方法；(c) Zeyde方法；(d) NE+LLE方法；(e) NE+NNLS方法；(f) SF方法；(g) ANR方法；(h)本文方法
Figure 4. SR reconstruction results of image "Baboon". (a) Original; (b) Bicubic; (c) Zeyde; (d) NE+LLE; (e) NE+NNLS; (f) SF; (g) ANR; (h) Proposed
图 5 图片PPT超分辨率重建效果图。(a)原图；(b) Bicubic方法；(c) Zeyde方法；(d) NE+LLE方法；(e) NE+NNLS方法；(f) SF方法；(g) ANR方法；(h)本文方法
Figure 5. SR reconstruction results of image "PPT". (a) Original; (b) Bicubic; (c) Zeyde; (d) NE+LLE; (e) NE+NNLS; (f) SF; (g) ANR; (h) Proposed
表 1 图片×2倍放大实验结果
Table 1. PSNR(dB) and SSIM values of super resolution images with upscaling factor 2
Bicubic Zeyde NE+LLE NE+NNLS SF ANR Proposed-1 Proposed Baboon PSNR 24.86 25.46 25.52 25.41 25.36 25.54 25.53 25.58 SSIM 0.6976 0.7513 0.7575 0.7497 0.7465 0.7586 0.7584 0.7639 Barbara PSNR 28.00 28.67 28.63 28.53 28.25 28.58 28.68 28.69 SSIM 0.8413 0.8724 0.8733 0.8691 0.8489 0.8729 0.8743 0.8753 Bridge PSNR 26.58 27.53 27.50 27.33 27.18 27.53 27.60 27.68 SSIM 0.7929 0.8178 0.8413 0.8343 0.8324 0.8422 0.8426 0.8468 Coastguard PSNR 29.12 30.42 30.38 30.08 29.59 30.42 30.51 30.59 SSIM 0.7893 0.8404 0.8435 0.8383 0.8150 0.8446 0.8444 0.8492 Comic PSNR 26.02 27.61 27.69 27.46 25.67 27.74 27.92 28.02 SSIM 0.8494 0.8979 0.9006 0.8951 0.8792 0.9011 0.9038 0.9062 Face PSNR 34.83 35.57 35.60 35.47 34.91 35.65 35.63 35.65 SSIM 0.8623 0.8818 0.8830 0.8801 0.8591 0.8841 0.8837 0.8851 Flowers PSNR 30.37 32.22 32.14 31.92 30.11 32.24 32.48 32.57 SSIM 0.8985 0.9271 0.9274 0.9238 0.9106 0.9287 0.9294 0.9301 Foreman PSNR 34.14 36.01 36.32 35.92 32.68 36.28 36.63 36.75 SSIM 0.9518 0.9664 0.9660 0.9656 0.9523 0.9665 0.9681 0.9675 Lenna PSNR 34.70 36.20 36.28 35.96 35.54 36.29 36.38 36.42 SSIM 0.9112 0.9262 0.9267 0.9242 0.9108 0.9275 0.9279 0.9280 Man PSNR 29.25 30.42 30.41 30.23 29.92 30.44 30.59 30.64 SSIM 0.8458 0.8775 0.8789 0.8740 0.8638 0.8797 0.8807 0.8823 Monarch PSNR 32.94 35.65 35.45 35.17 33.30 35.61 36.28 36.38 SSIM 0.9601 0.9726 0.9716 0.9709 0.9583 0.9726 0.9741 0.9730 Pepper PSNR 34.97 36.55 36.38 36.24 35.76 36.36 36.64 36.72 SSIM 0.9073 0.9190 0.9184 0.9172 0.9039 0.9190 0.9200 0.9196 PPT PSNR 26.87 29.29 28.92 29.07 25.27 28.93 29.55 29.66 SSIM 0.9450 0.9697 0.9648 0.9662 0.9421 0.9651 0.9711 0.9706 Zebra PSNR 30.63 33.20 33.02 32.60 26.77 33.05 33.33 33.44 SSIM 0.9086 0.9381 0.9387 0.9342 0.9131 0.9393 0.9400 0.9414 Average PSNR 30.23 31.77 31.73 31.53 30.02 31.76 31.98 32.06 SSIM 0.8687 0.8970 0.8994 0.8959 0.8811 0.9001 0.9013 0.9028 
下载: 导出CSV
表 2 不同放大倍数的实验结果
Table 2. Average PSNR(dB) and SSIM values of different upscaling factor
Scale Bicubic Yang Zeyde NE+LLE NE+NNLS SF ANR Proposed ×2 PSNR 30.23 - 31.77 31.73 31.53 30.02 31.76 32.06 SSIM 0.8687 - 0.8970 0.8994 0.8959 0.8811 0.9001 0.9028 ×3 PSNR 27.54 28.31 28.66 28.57 28.47 27.25 28.62 28.79 SSIM 0.7736 0.7954 0.8078 0.8075 0.8032 0.7856 0.8089 0.8123 ×4 PSNR 26.00 25.93 26.81 26.78 26.80 25.22 26.82 26.92 SSIM 0.7019 0.6958 0.7342 0.7332 0.7323 0.6845 0.7346 0.7359
下载: 导出CSV
表 3 不同算法的图像重建时间
Table 3. Time complexity of different methods
s Images Yang Zeyde NE+LLE NE+NNLS SF ANR Proposed Baboon 69.79 2.36 3.63 16.97 61.06 0.91 6.19 Barbara 73.99 3.95 6.27 29.92 77.94 1.51 11.43 Bridge 82.25 2.45 3.90 18.24 21.86 0.91 6.91 Coastguard 20.54 0.94 1.50 7.14 21.86 0.35 2.41 Comic 29.39 0.80 1.30 6.13 26.11 0.32 2.31 Face 11.77 0.68 1.12 5.14 11.81 0.26 1.98 Flowers 43.25 1.66 2.69 12.45 41.26 0.63 4.88 Foreman 15.50 0.93 1.47 6.93 18.11 0.35 2.58 Lenna 39.31 2.49 3.91 18.98 41.34 0.95 6.59 Man 59.18 2.42 3.89 18.48 57.74 0.91 7.25 Monarch 62.24 3.67 5.87 27.76 53.84 1.37 10.18 Pepper 36.77 2.43 3.87 18.82 38.51 0.92 7.01 Ppt 52.06 2.95 5.01 22.11 52.51 1.19 9.01 Zebra 62.71 2.10 3.36 15.79 57.52 0.78 6.00 Average 47.05 2.13 3.41 16.06 41.53 0.81 6.05
下载: 导出CSV
-
参考文献
[1] Park S C, Park M K, Kang M G. Super-resolution image reconstruction: a technical overview[J]. IEEE Signal Processing Magazine, 2003, 20(3): 21–36. doi: 10.1109/MSP.2003.1203207
[2] 詹曙, 方琪.边缘增强的多字典学习图像超分辨率重建算法[J].光电工程, 2016, 43(4): 40–47. http://www.cnki.com.cn/Article/CJFDTotal-GDGC201604008.htm
Zhan S, Fang Q. Image super-resolution based on edge-enhancement and multi-dictionary learning[J]. Opto-Electronic Engineering, 2016, 43(4): 40–47. http://www.cnki.com.cn/Article/CJFDTotal-GDGC201604008.htm
[3] 苏衡, 周杰, 张志浩.超分辨率图像重建方法综述[J].自动化学报, 2013, 39(8): 1202–1213. http://www.doc88.com/p-3337348238357.html
Su H, Zhou J, Zhang Z H. Survey of super-resolution image reconstruction methods[J]. Acta Automatica Sinica, 2013, 39(8): 1202–1213. http://www.doc88.com/p-3337348238357.html
[4] Tsai R Y. Multiframe image restoration and registration[J]. Advances in Computer Vision and Image Processing, 1984, 1(2): 317–339. https://dl.acm.org/citation.cfm?id=825197
[5] 吴从中, 胡长胜, 张明君, 等.有监督多类字典学习的单幅图像超分辨率重建[J].光电工程, 2016, 43(11): 69–75. doi: 10.3969/j.issn.1003-501X.2016.11.011
Wu C Z, Hu C S, Zhang M J, et al. Single image super-resolution reconstruction via supervised multi-dictionary learning[J]. Opto-Electronic Engineering, 2016, 43(11): 69–75. doi: 10.3969/j.issn.1003-501X.2016.11.011
[6] 汪荣贵, 汪庆辉, 杨娟, 等.融合特征分类和独立字典训练的超分辨率重建[J].光电工程, 2018, 45(1): 170542. doi: 10.12086/oee.2018.170542 http://www.oejournal.org/J/OEE/Article/Details/A180213000010/CN
Wang R G, Wang Q H, Yang J, et al. Image super-resolution reconstruction by fusing feature classification and independent dictionary training[J]. Opto-Electronic Engineering, 2018, 45(1): 170542. doi: 10.12086/oee.2018.170542 http://www.oejournal.org/J/OEE/Article/Details/A180213000010/CN
[7] Freeman W T, Jones T R, Pasztor E C. Example-based super-resolution[J]. IEEE Computer Graphics and Applications, 2002, 22(2): 56–65. doi: 10.1109/38.988747
[8] Chang H, Yeung D Y, Xiong Y M. Super-resolution through neighbor embedding[C]//Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2004: I.
[9] Roweis S T, Saul L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290(5500): 2323–2326. doi: 10.1126/science.290.5500.2323
[10] Yang J C, Wright J, Huang T S, et al. Image super-resolution via sparse representation[J]. IEEE Transactions on Image Processing, 2010, 19(11): 2861–2873. doi: 10.1109/TIP.2010.2050625
[11] Zeyde R, Elad M, Protter M. On single image scale-up using sparse-representations[C]//International Conference on Curves and Surfaces, Berlin, Heidelberg, 2010, 6920: 711–730.
[12] Aharon M, Elad M, Bruckstein A. rmK-SVD: An algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311–4322. doi: 10.1109/TSP.2006.881199
[13] Yang C Y, Yang M H. Fast direct super-resolution by simple functions[C]//Proceedings of 2013 IEEE International Conference on Computer Vision, 2013: 561–568.
[14] Zhang L, Yang M, Feng X C. Sparse representation or collaborative representation: Which helps face recognition[C]// Proceedings of 2011 IEEE International Conference on Computer Vision, 2011: 471–478.
[15] Timofte R, De Smet V, Van Gool L. Anchored neighborhood regression for fast example-based super-resolution[C]// Proceedings of 2013 IEEE International Conference on Computer Vision, 2013: 1920–1927.
[16] Irani M, Peleg S. Improving resolution by image registration[J]. CVGIP: Graphical Models and Image Processing, 1991, 53(3): 231–239. doi: 10.1016/1049-9652(91)90045-L
[17] Bevilacqua M, Roumy A, Guillemot C, et al. Low-complexity single-image super-resolution based on nonnegative neighbor embedding[C]// Proceedings British Machine Vision Conference, 2012: 135.
-
访问统计
点击扫一扫
图(7)
表(3)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
