E-mail Alert
RSS
Decoupling study and noise analysis of multi-degree-of-freedom deformation measurement method for space gravitational wave detection telescope
-
摘要
空间引力波探测望远镜是引力波探测卫星的核心载荷之一，它同时对传输光束进行扩束和缩束。光程稳定性是望远镜的核心指标之一，其与望远镜结构稳定性密切相关。为了满足引力波探测任务对望远镜提出的超高光程稳定性和结构稳定性要求，必须对望远镜结构形变测量进行研究。本文开展了对空间引力波探测望远镜多自由度形变测量的研究，重点解决多自由度测量的耦合问题，并对误差来源进行详细分析。在空间引力波探测望远镜的研制阶段，该测量方法的研究有望满足望远镜多自由度形变测量的需求，为望远镜设计提供多自由度形变的数据反馈，为望远镜光程稳定性研究提供指导。
-
关键词:
- 空间引力波探测望远镜 /
- 形变测量 /
- 多自由度 /
- 解耦研究 /
- 噪声分析
Abstract
The space gravitational wave telescope is a key payload of gravitational wave detection satellites, responsible for both beam expansion and compression. Optical path stability is a crucial indicator for the telescope, closely related to its structural stability. To meet the stringent requirements for ultra-high optical path stability and structural stability in gravitational wave detection missions, it is necessary to investigate the measurement of structural deformations in the telescope. This paper presents a study on multi-degree of freedom deformation measurement for space gravitational wave telescopes, focusing on addressing the coupling issues in multi-degree of freedom measurement and conducting a detailed analysis of error sources. During the development phase of the space gravitational wave telescope, this measurement method is expected to meet the demands for multi-degree of freedom deformation measurement, providing data feedback on multi-degree of freedom deformations for telescope design and offering guidance for optical path stability research.
-
Overview
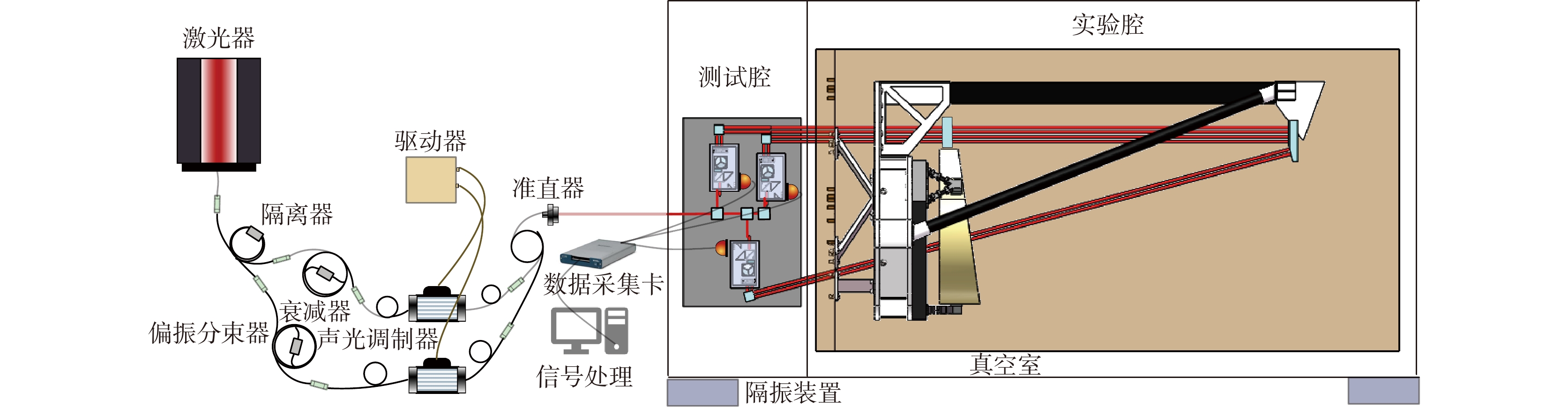
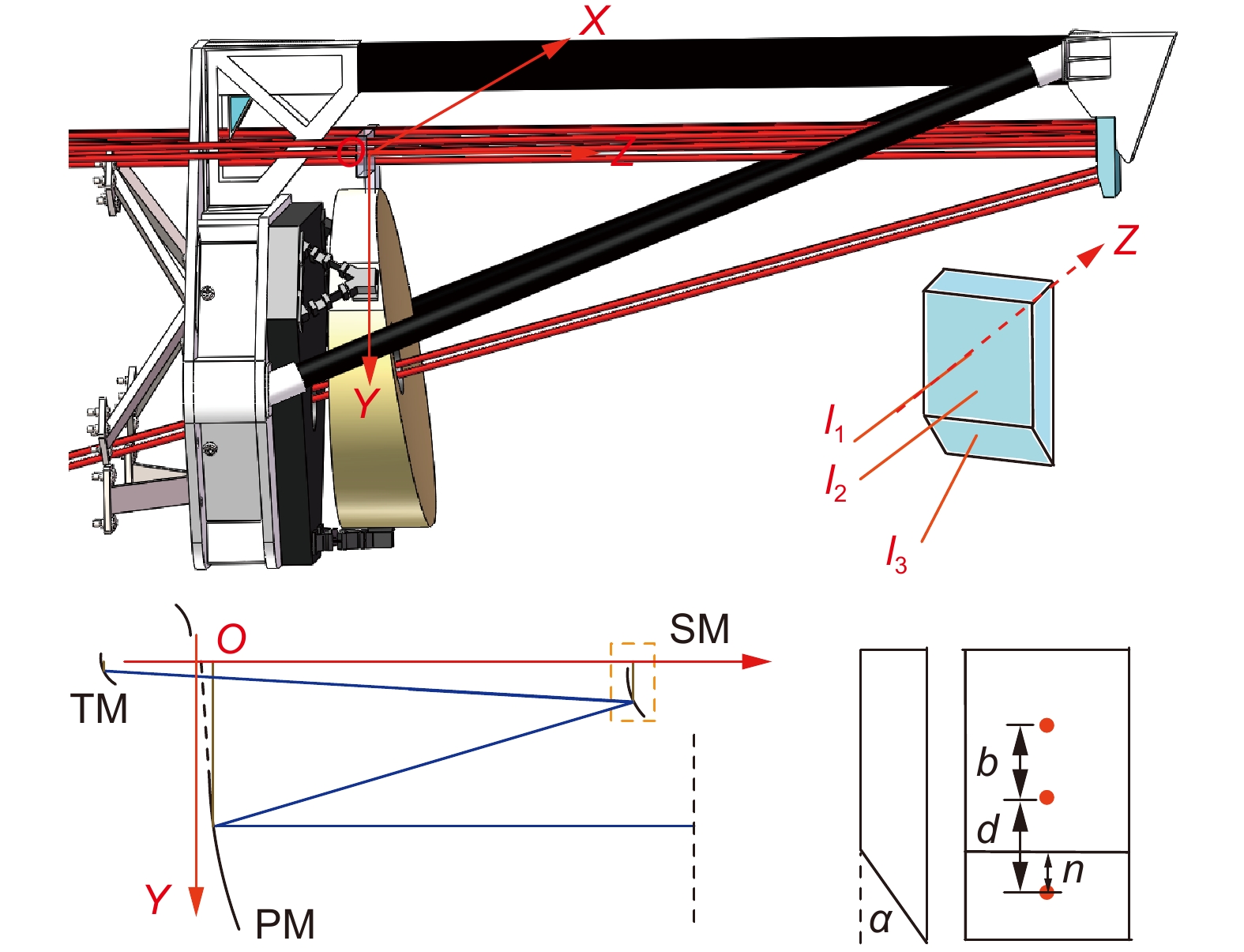
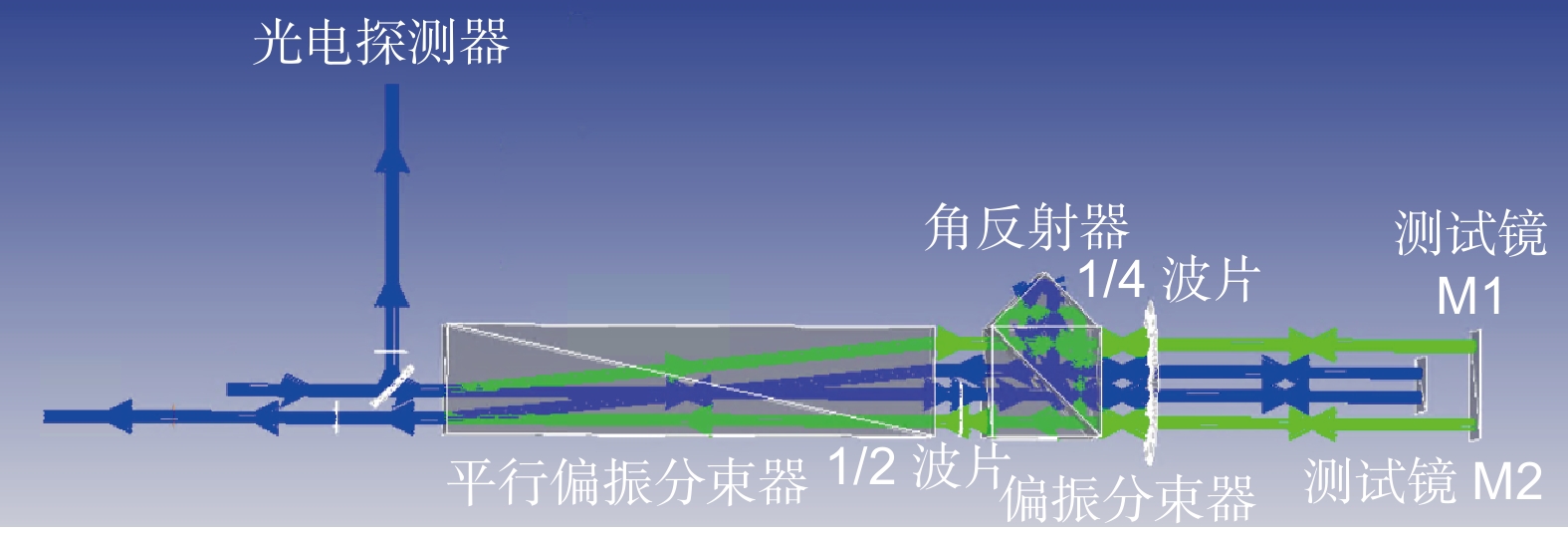
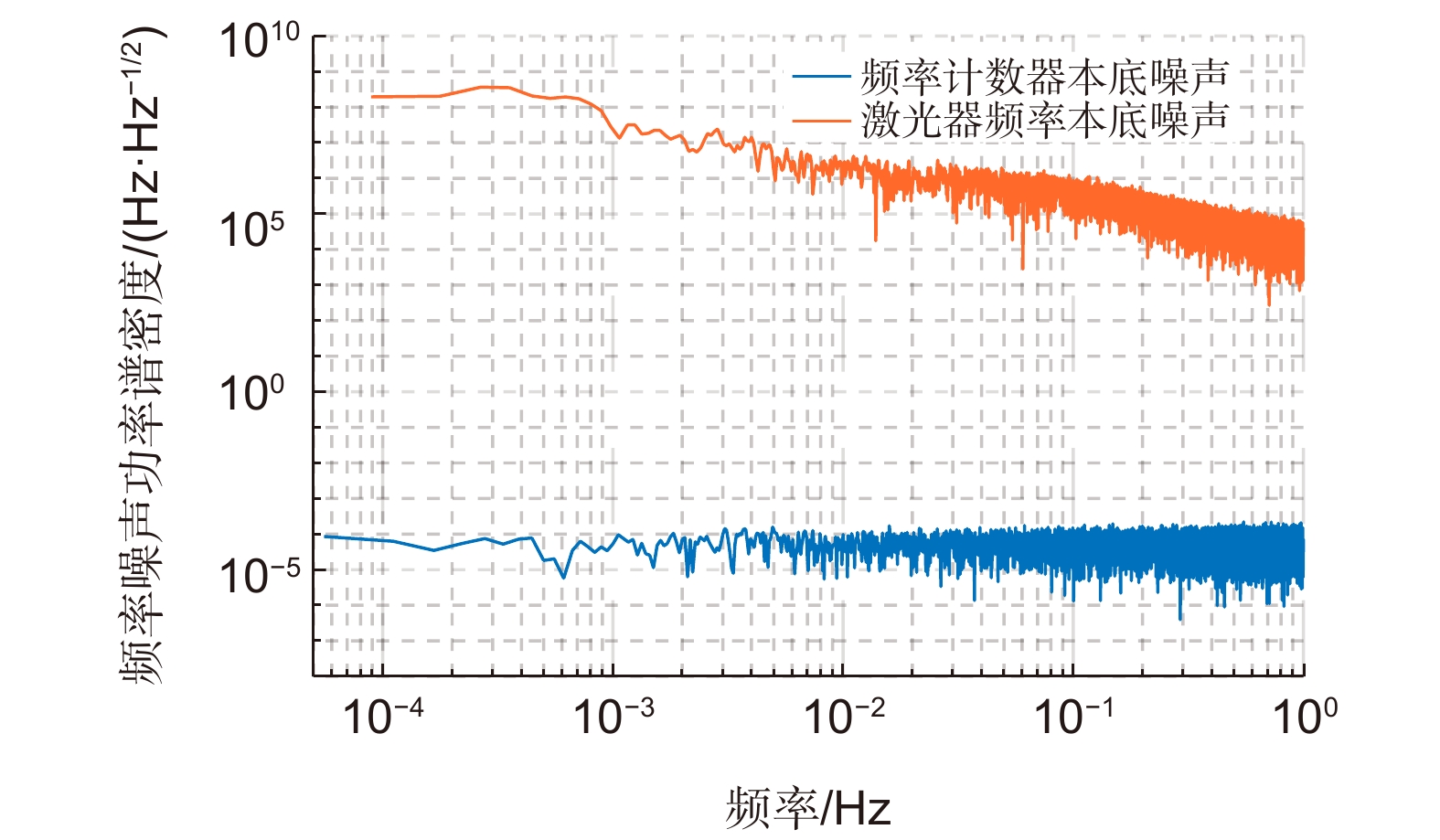
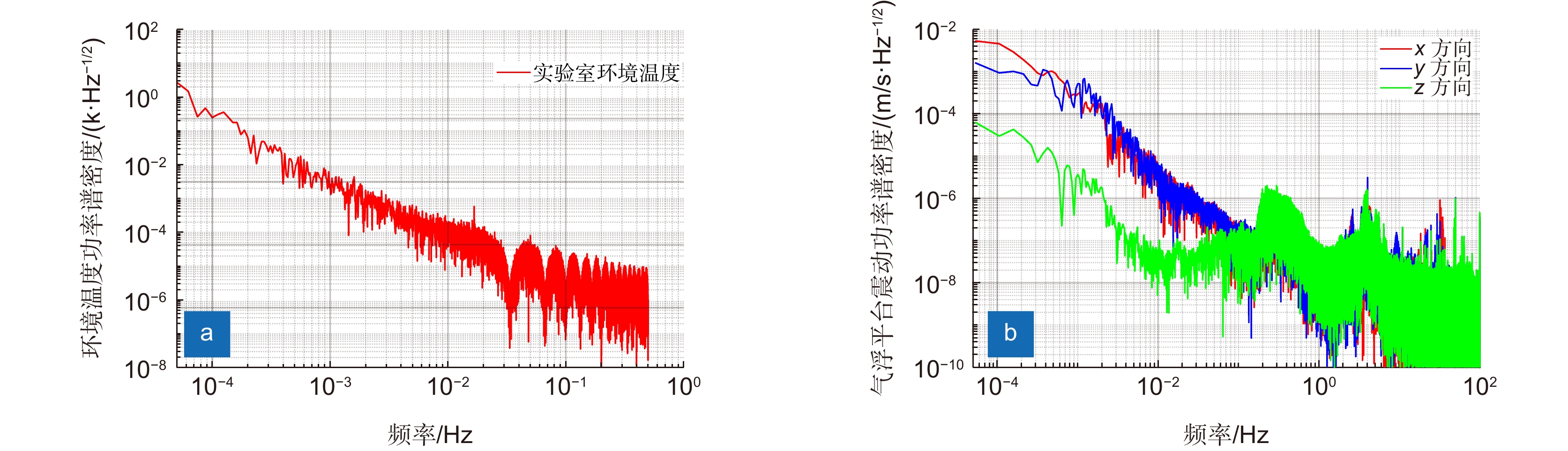
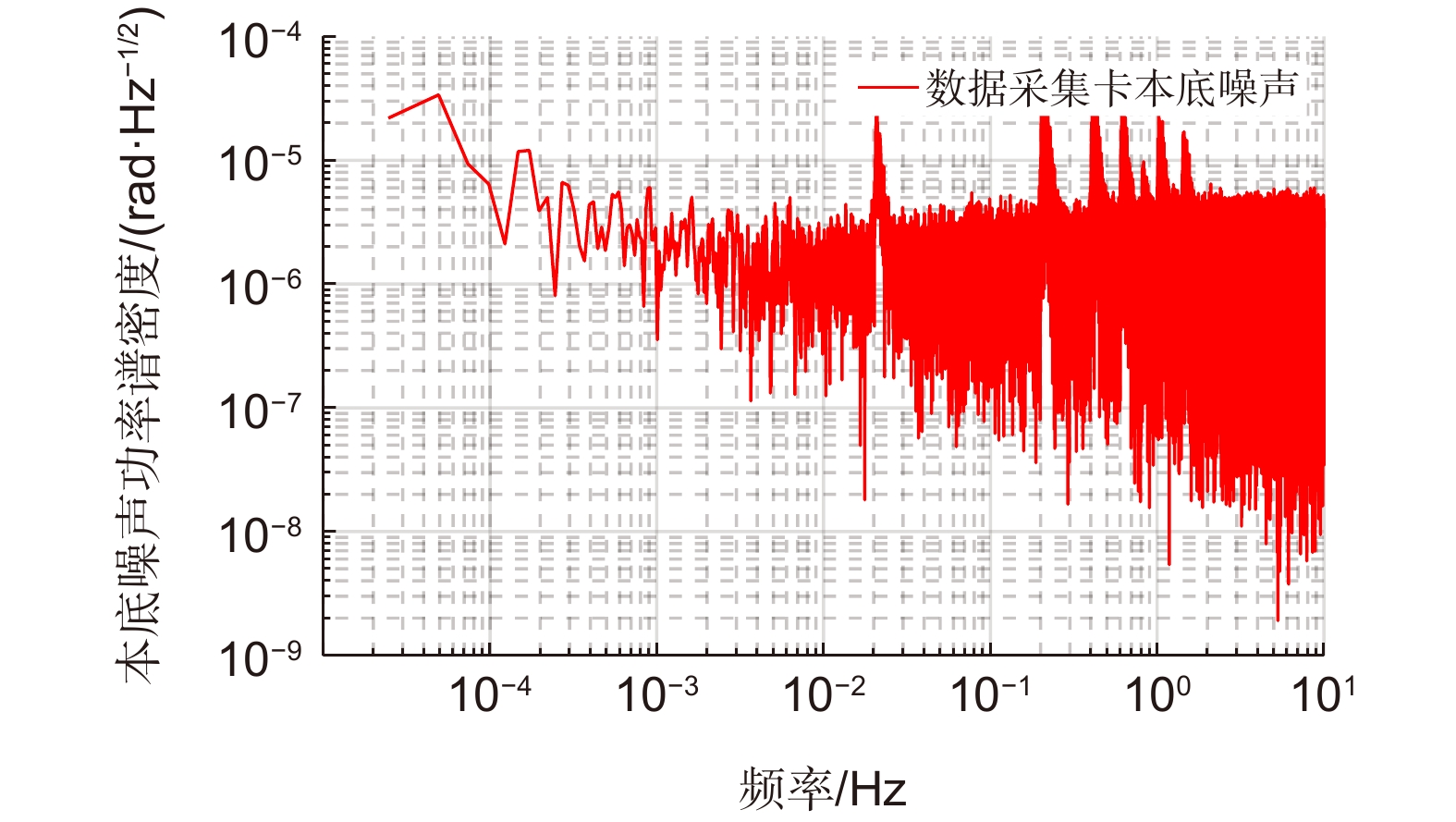
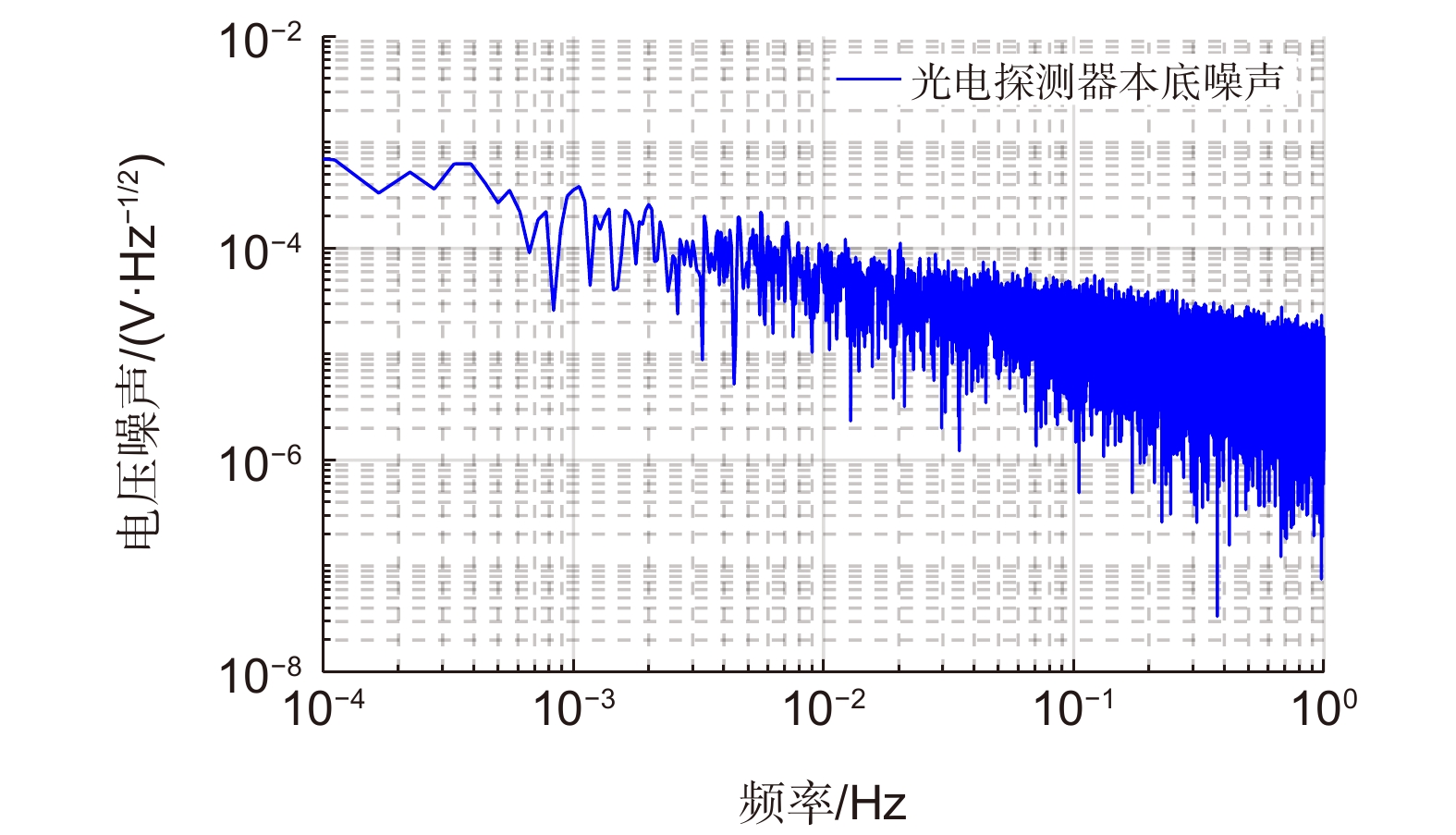
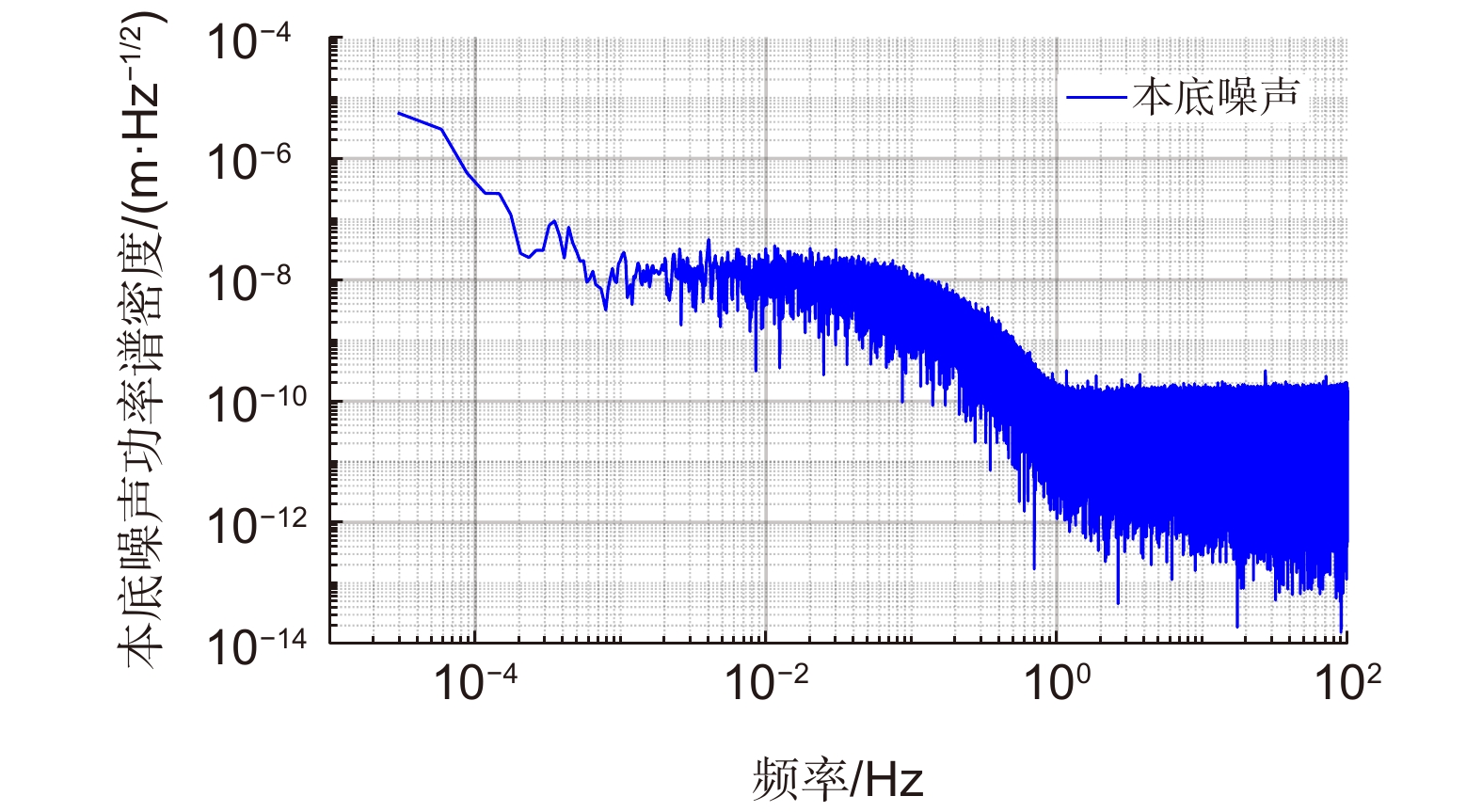
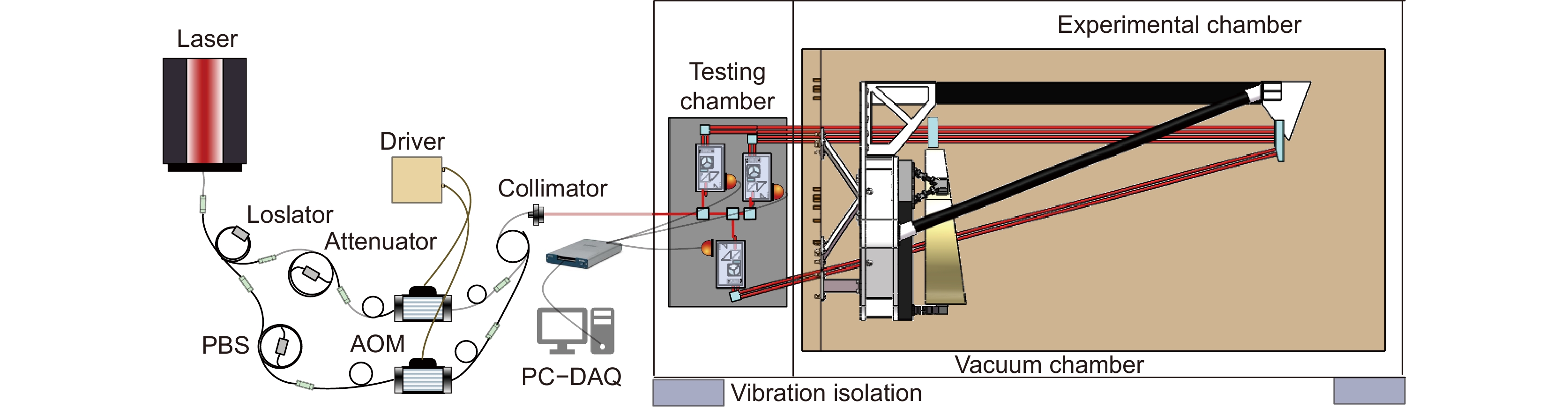
Overview: The space gravitational wave detection telescope is one of the core payloads of the gravitational wave detection satellite, simultaneously expanding and contracting the transmitted beam. Optical path stability is one of the core indices for the telescope, closely related to its structural stability. To meet the ultra-high path stability and structural stability requirements posed by the gravitational wave detection mission, it is essential to study the structural deformation measurement of the telescope. Currently, there are still several shortcomings in the research of multi-degree-of-freedom deformation measurement methods for gravitational wave detection telescopes, such as inaccurate selection of measurement points, inability to decouple multi-degree-of-freedom coupling, and unclear identification of error sources in multi-degree-of-freedom measurement. This paper deeply investigates the high-precision measurement of structural deformation of space-borne telescopes designed for space gravitational wave detection. It preliminarily establishes a framework and method system for measuring the structural deformation of space-borne telescopes, theoretically describing the measurement principle of the method. The feasibility of this method applied to space gravitational wave detection is verified through simulation analysis and error decomposition. The paper focuses on resolving the issue of decoupling multiple degrees of freedom, establishing a mathematical model using analytical methods, and conducting preliminary validation using Zemax. Finally, noise analysis of the measurement system is carried out, with experimental testing of the main noise components in the measurement system, validating the correctness of the theoretical noise model proposed in this paper. The experimental results show that near 1 Hz, the displacement noise background of the single-link interferometer is 100 pm/Hz1/2. At 1 mHz in the low-frequency range, the displacement noise background reaches 10 nm/Hz1/2. The noise level of the measurement system below 1 mHz is mainly limited by environmental temperature noise, while above 10 mHz, it is primarily constrained by laser frequency noise, phase acquisition background noise, and vibration noise. During the development phase of the space gravitational wave detection telescope, the research on this measurement method is expected to fulfill the telescope's multi-degree-of-freedom deformation measurement needs. It also provides data feedback for telescope design and offers guidance for the study of the telescope's optical path stability.
-
-
图 1 三自由度形变测量系统结构组成示意图
Figure 1. Schematic diagram of the composition of a three-degree-of-freedom deformation measurement system
图 2 三自由度形变测量系统示意图
Figure 2. Schematic diagram of the three-degree-of-freedom deformation measurement system
图 4 三自由度形变测量解耦数学模型示意图
Figure 4. Schematic diagram of the decoupling mathematical model for the three-degree-of-freedom deformation measurement system
图 7 (a) 实际测量光路示意图；(b) Zemax光路建模图
Figure 7. (a) Schematic diagram of the actual measurement path; (b) Zemax optical path modeling diagram
图 9 实验室温度与振动水平。(a) 温度测试图；(b) 振动测试图
Figure 9. Laboratory temperature and vibration level. (a) Temperature test chart; (b) Vibration test chart
表 1 多自由度测量方法的优缺点
Table 1. Advantages and disadvantages of multiple-degree-of-freedom measurement methods
下载: 导出CSV
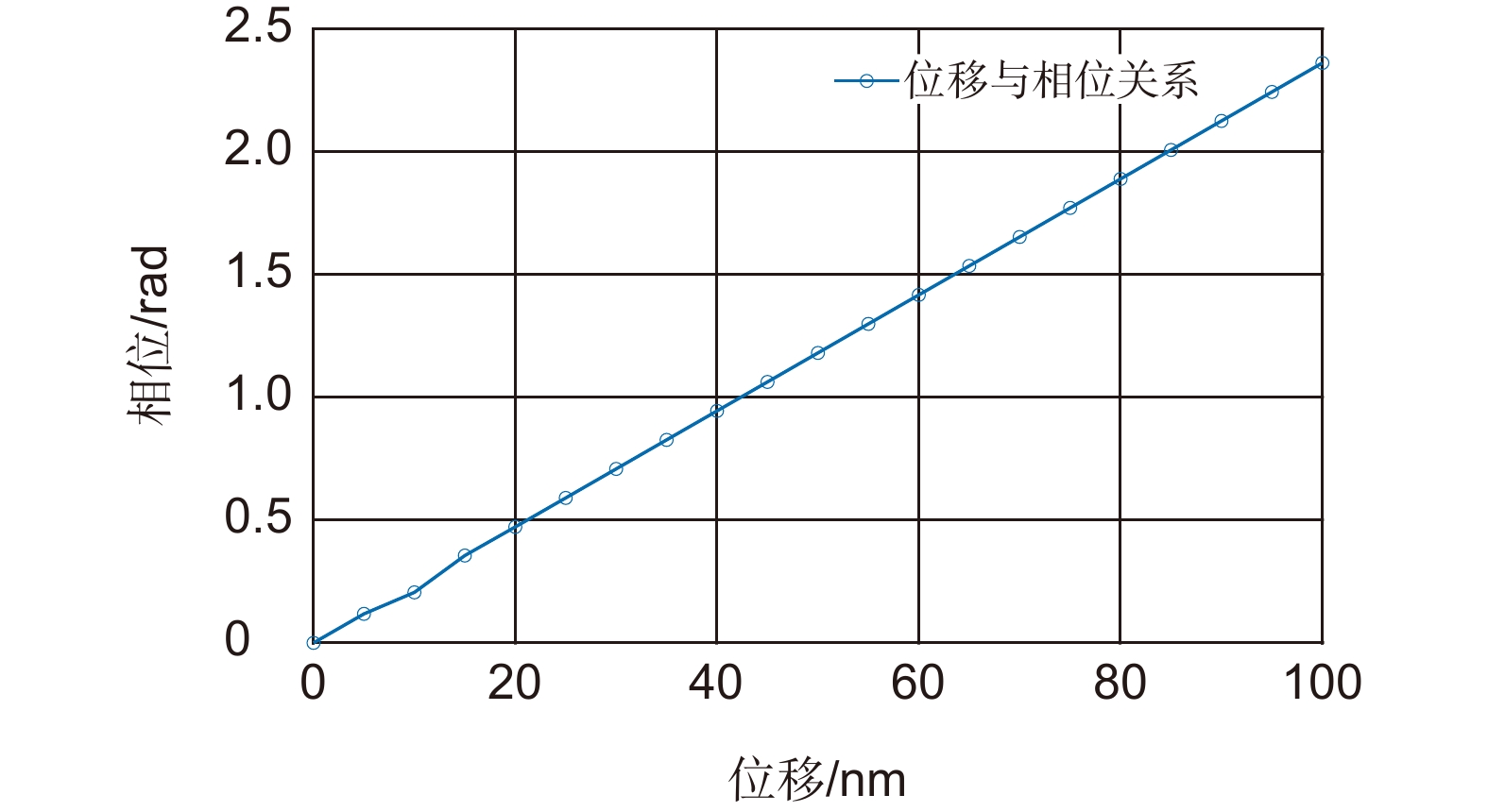
表 2 测试镜刚体位移与光电探测器相位差关系
Table 2. Test the relationship between the rigid body displacement of the mirror and the phase difference received by the photodetector
相对位移 相位差 PD1 PD2 PD3 初始位置 0 0 0 沿光轴方向+z平移20 nm 0.47 0.47 0 Rx方向旋转1.7 µrad 0.66 0.47 0.61 垂直光轴方向+y平移20 nm 0 0 0.30
下载: 导出CSV
表 3 多自由度测量系统误差灵敏度分析
Table 3. Error sensitivity analysis of the measurement system with multiple degrees of freedom
自由度 比值 z dI : S : α = 1 : 0 : 0 Rx dI : S : α= 10000 : 1 : 0 y dI : S : α= 10000 : 1 : 1
下载: 导出CSV
表 4 望远镜形变测量系统测量光程噪声指标分配及要求
Table 4. Allocation and requirements of optical path noise indicators for the telescope deformation measurement system
测量系统组成部分 主要噪声源 噪声分配
(nm/Hz1/2@1 mHz)备注 激光光源 激光频率噪声 3 要求激光频率噪声δf小于4.2×107<Hz/Hz1/2@1 mHz 前端光程耦合噪声 声光调制耦合噪声 1 等效位移噪声<1 nm/Hz1/2@1 mHz 光纤温度耦合噪声 2 光纤温度波动δT≤15 mK/Hz1/2@1 mHz 集成光学
器件平台温度位移耦合噪声 8 温度位移耦合系数dS/dT=70 nm/K，测试环境温度波动δT≤15 mK/Hz1/2@1 mHz 振动位移耦合噪声 2 振动位移耦合系数dS/dx=0.3×10−3 m/m，测试环境振动波动δX≤1×10−3 m/s /Hz1/2@1 mHz 空气折射率噪声 2 温度波动δT≤15 mK/Hz1/2@1 mHz 偏振噪声 2 等效位移噪声<2 nm/Hz1/2@1 mHz 杂散光噪声 3 控制杂散光强度相较于主光束低于−20 dB 信号采集
数据处理探测器耦合噪声 1 相对强度噪声需低于−100 dB/Hz@1 mHz 相位读取噪声 0.01 要求相位计等效位移本底噪声是0.01 nm/Hz1/2@1 mHz 测量系统总体噪声 10
下载: 导出CSV
-
参考文献
[1] Abbott B P, Abbott R, Abbott T D, et al. Observation of gravitational waves from a binary black hole merger[J]. Phys Rev Lett, 2016, 116(6): 061102. doi: 10.1103/PhysRevLett.116.061102
[2] Danzmann K, The LISA Study Team. LISA: laser interferometer space antenna for gravitational wave measurements[J]. Class Quantum Grav, 1996, 13(11A): A247. doi: 10.1088/0264-9381/13/11A/033
[3] Luo J, Chen L S, Duan H Z, et al. TianQin: a space-borne gravitational wave detector[J]. Class Quantum Grav, 2016, 33(3): 035010. doi: 10.1088/0264-9381/33/3/035010
[4] Luo J, Bai Y Z, Cai L, et al. The first round result from the TianQin-1 satellite[J]. Class Quantum Grav, 37(18): 185013. https://doi.org/10.1088/1361-6382/aba66a.
[5] Livas J, Sankar S. Optical telescope design study results[J]. J Phys Conf Ser, 2015, 610: 012029. doi: 10.1088/1742-6596/610/1/012029
[6] 王小勇,白绍竣,张倩,等. 空间引力波探测望远镜研究进展[J]. 光电工程, 2023, 50(11): 230219. doi: 10.12086/oee.2023.230219
Wang X Y, Bai S J, Zhang Q, et al. Research progress of telescopes for space-based gravitational wave missions[J]. Opto-Electron Eng, 2023, 50(11): 230219. doi: 10.12086/oee.2023.230219
[7] J. Sanjuán; A. Preston; D. Korytov, et al. Carbon fiber reinforced polymer dimensional stability investigations for use on the laser interferometer space antenna mission telescope[J]. Rev Sci Instrum, 2011, 82(12): 124501.
[8] Desnoyers N, Goyette P, Leduc B, et al. Dimensional stability performance of a CFRP sandwich optical bench for microsatellite payload[J]. Proc SPIE, 2017, 10372: 103720G. doi: 10.1117/12.2274311
[9] 范纹彤, 赵宏超, 范磊, 等. 空间引力波探测望远镜系统技术初步分析[J]. 中山大学学报(自然科学版), 2021, 60(1-2): 178−185. doi: 10.13471/j.cnki.acta.snus.2020.11.02.2020B111
Fan W T, Zhao H C, Fan L, et al. Preliminary analysis of space gravitational wave detection telescope system technology[J]. Acta Sci Nat Univ Sunyatseni, 2021, 60(1-2): 178−185. doi: 10.13471/j.cnki.acta.snus.2020.11.02.2020B111
[10] Machado J C, Heinrich T, Schuldt T, et al. Picometer resolution interferometric characterization of the dimensional stability of zero CTE CFRP[J]. Proc SPIE, 2008, 7018: 70183D. doi: 10.1117/12.789495
[11] Spannagel R, Hamann I, Sanjuan J, et al. Dilatometer setup for low coefficient of thermal expansion materials measurements in the 140 K-250 K temperature range[J]. Rev Sci Instrum, 2016, 87(10): 103112. doi: 10.1063/1.4965813.
[12] Spannagel R, Gohlke M, Schuldt T, et al. CTE measurement setup with 10 ppb/K sensitivity for characterizing lightweight and highly stable materials for space applications[J]. Proc SPIE, 2012, 8450: 84500Q. doi: 10.1117/12.926061
[13] Sanjuán J, Korytov D, Mueller G, et al. Note: silicon carbide telescope dimensional stability for space-based gravitational wave detectors[J]. Rev Sci Instrum, 2012, 83(11): 116107. doi: 10.1063/1.4767247
[14] Verlaan A L, Hogenhuis H, Pijnenburg J, et al. LISA telescope assembly optical stability characterization for ESA[J]. Proc SPIE, 2012, 8450: 845003. doi: 10.1117/12.925112
[15] Sang B L, Deng X Q, Peng B, et al. Dimensional stability ground test and in-orbit prediction of SiC telescope frame for space gravitational wave detection[J]. IEEE Access, 2022, 10: 21041−21047. doi: 10.1109/ACCESS.2022.3152490
[16] 李博宏, 罗健, 丘敏艳, 等. 引力波探测望远镜超低热变形桁架支撑结构设计技术[J]. 光电工程, 2023, 50(11): 230155. doi: 10.12086/oee.2023.230155
Li B H, Luo J, Qiu M Y, et al. Design technology of the truss support structure of the ultra-low thermal deformation gravitational wave detection telescope[J]. Opto-Electron Eng, 2023, 50(11): 230155. doi: 10.12086/oee.2023.230155
[17] Yu X Z. Multi-degree of freedom optical metrology techniques[D]. Rochester: University of Rochester, 2017.
[18] Klop W A, Verlaan A L. Dimensional stability testing in thermal vacuum of the CHEOPS optical telescope assembly[J]. Proc SPIE, 2016, 9904: 990437. doi: 10.1117/12.2232899
[19] 颜浩. 基于激光干涉的高精度多自由度光学传感研究[D]. 武汉: 华中科技大学, 2019.
Yan H. Study on ultra-precision multi-degree-of-freedom optical measurement base on laser interferometry[D]. Wuhan: Huazhong University of Science and Technology, 2019.
[20] 余建平. 面向精密定位的平面电容式多自由度位移测量传感器关键技术研究[D]. 杭州: 浙江大学, 2013.
Yu J P. Study on planar capacitive sensors for multiple-dimensional precision displacement measurement[D]. Hangzhou: Zhejiang University, 2013.
[21] 孙闯. 面向精密工程的多自由度测量方法研究[D]. 长春: 中国科学院大学(中国科学院长春光学精密机械与物理研究所), 2021.
Sun C. Research on multi-degree-of-freedom measurement method for precision engineering[D]. Changchun: Changchun Institute of Optics, Fine Mechanics and Physics Chinese Academy of Sciences, 2021.
[22] 赵凯, 范纹彤, 海宏文, 等. 望远镜光程稳定性测量方案设计及噪声理论分析[J]. 光电工程, 2023, 50(11): 230158. doi: 10.12086/oee.2023.230158
Zhao K, Fan W T, Hai H W, et al. Design of optical path stability measurement scheme and theoretical analysis of noise in telescope[J]. Opto-Electron Eng, 2023, 50(11): 230158. doi: 10.12086/oee.2023.230158
-
访问统计
点击扫一扫
图(13)
表(4)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
