E-mail Alert
RSS
Design theory and method of off-axis four-mirror telescope for space-based gravitational-wave mission
-
摘要
用于空间引力波探测的星载望远镜在航天器间进行激光的传输以支持精密干涉测量系统，因此望远镜的光程稳定性已经成为一项关键的技术指标。在此系统中，光瞳像差与传统的像平面像差相比在了解系统光程稳定性需求、评价望远镜成像质量以及抑制抖动光程耦合噪声等方面可提供更深刻的见解。本文基于传统像平面像差理论和光瞳像差理论，建立了望远镜的初始结构，然后利用光学软件Zemax的宏编程实现了光瞳像差和像平面像差的自动校正，从而实现了高性能星载望远镜的设计，仿真结果显示满足天琴任务的需求。
Abstract
The telescopes for space-based gravitational wave detection are used to transmit the laser beam between spacecraft to support the precise interference measurement system. Therefore, the optical path stability of the telescope has become a crucial technical parameter. In this system, pupil aberrations provide deeper insights compared to traditional image plane aberrations in understanding optical path stability requirements, evaluating telescope imaging quality, and suppressing tilt-to-length coupling noise. Based on the theory of traditional imaging aberration and pupil aberration theory, the initial structure of the telescope is established, and the automatic correction of pupil aberration and image plane aberration is achieved through macro programming in the commercial optical software Zemax, thus achieving the design of a high-performance spaceborne telescope. Simulation results demonstrate that the design can meets the requirements of the TianQin mission.
-
Overview
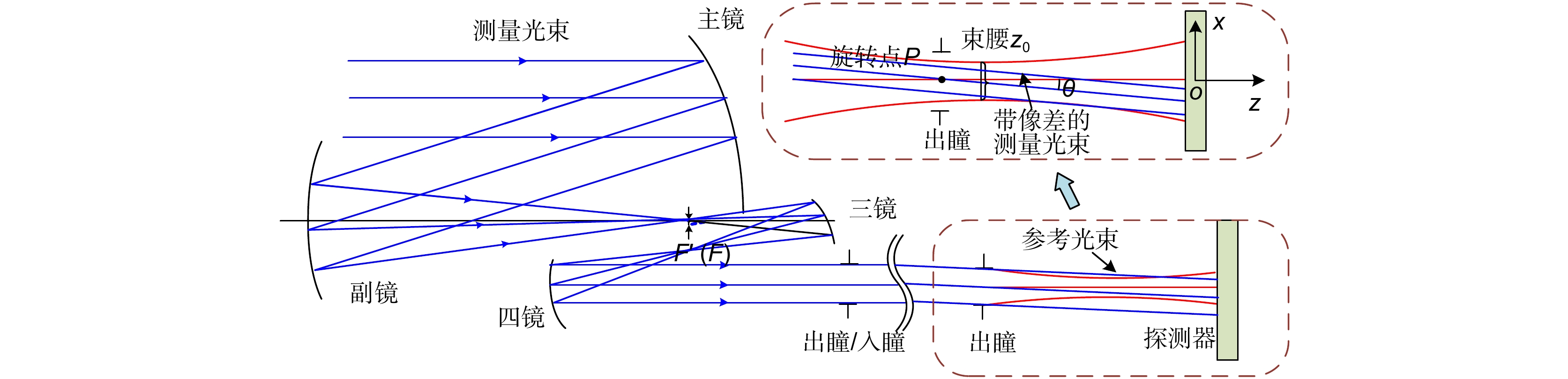
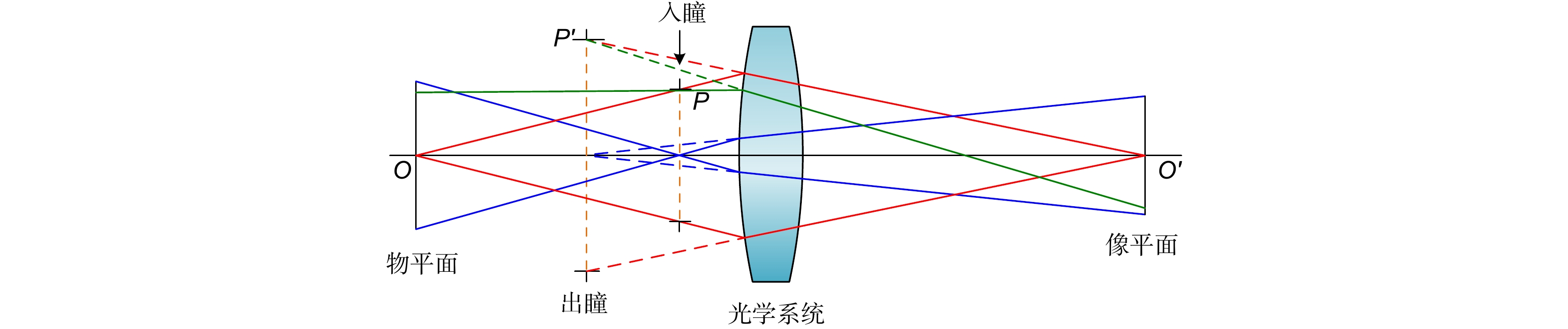
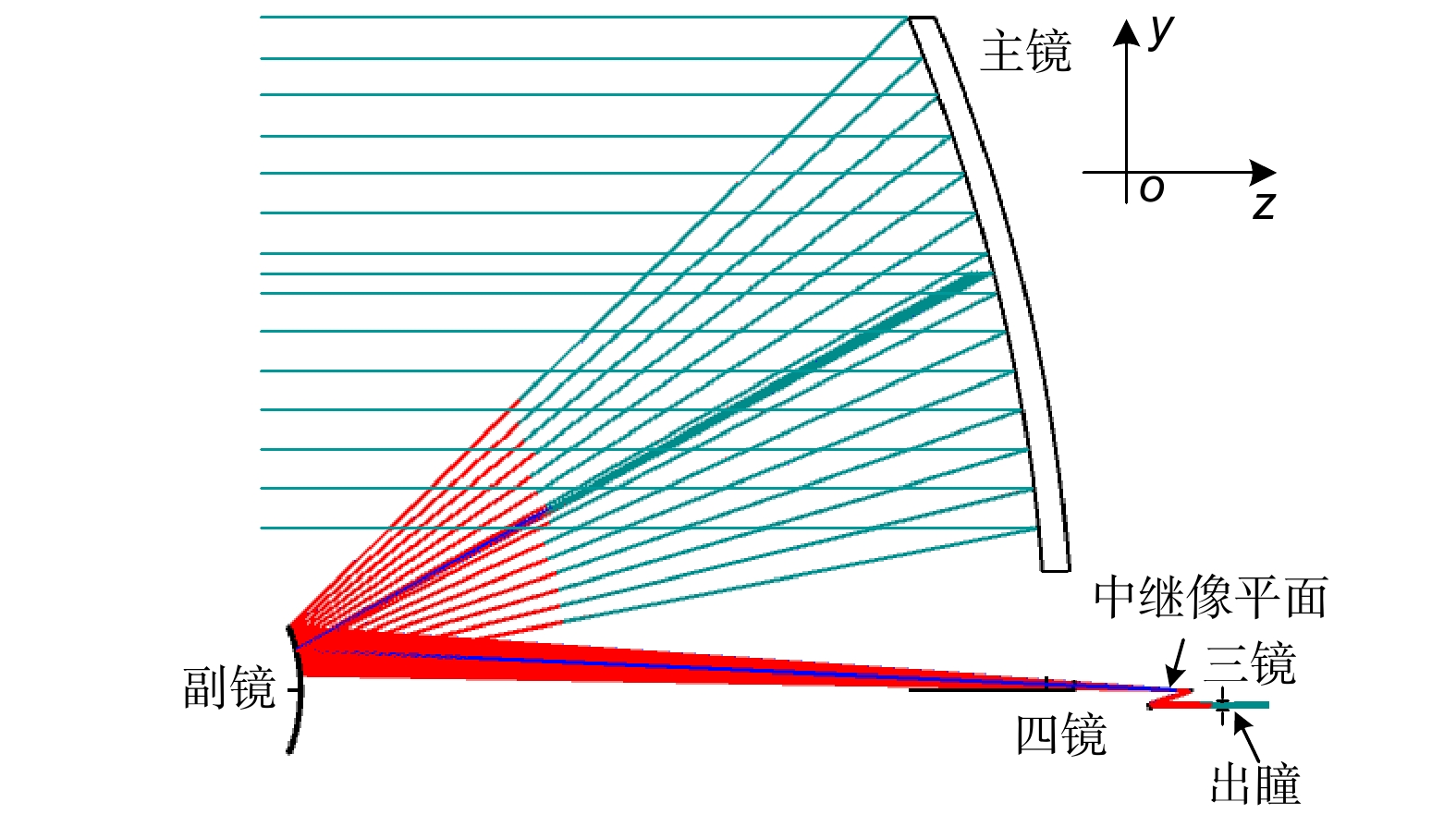
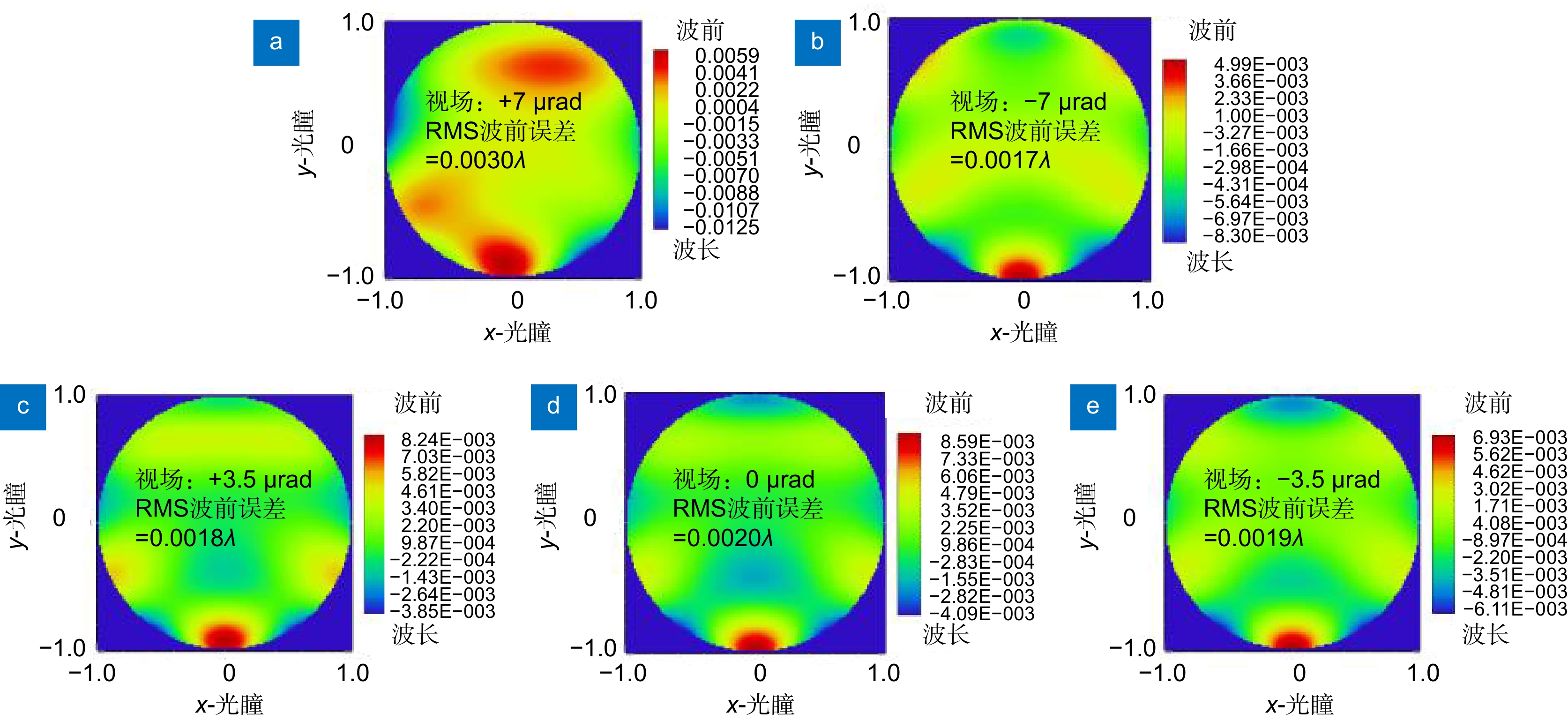
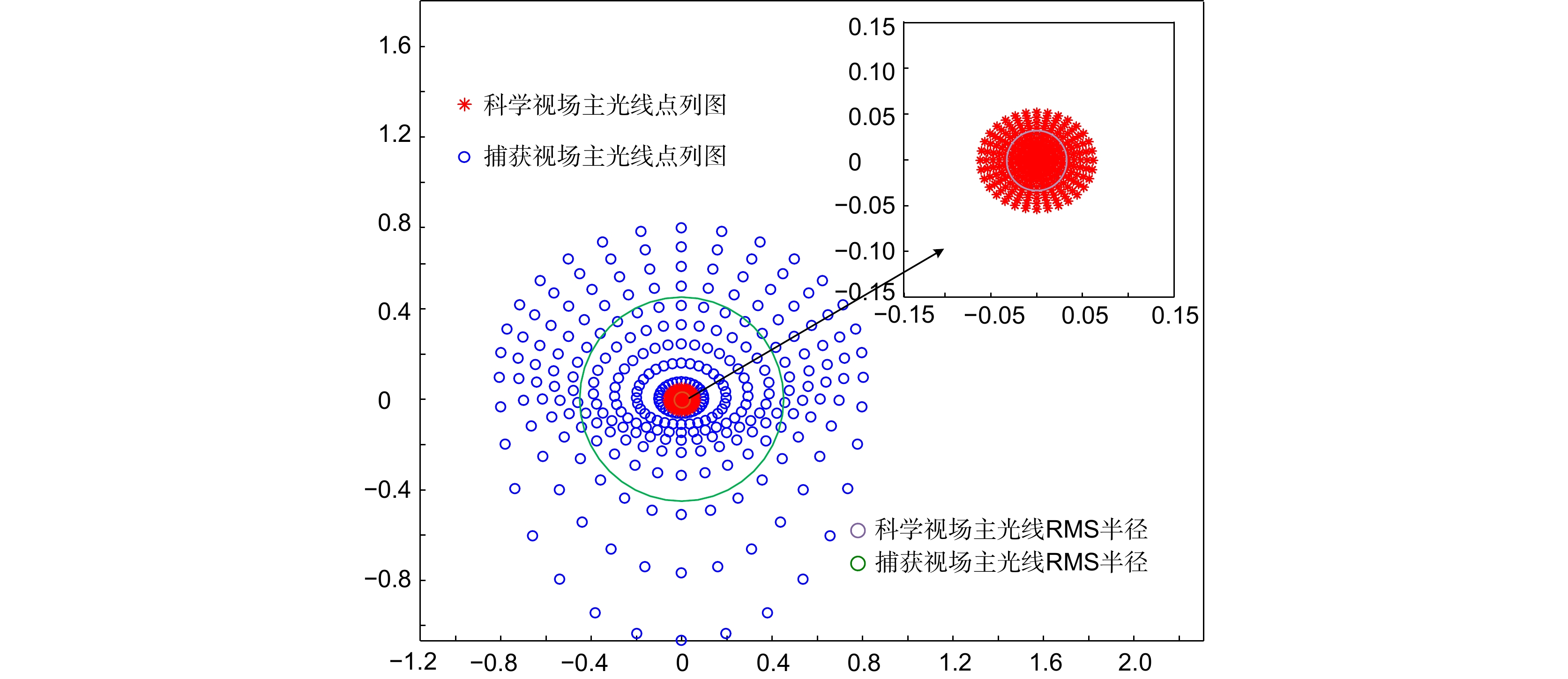
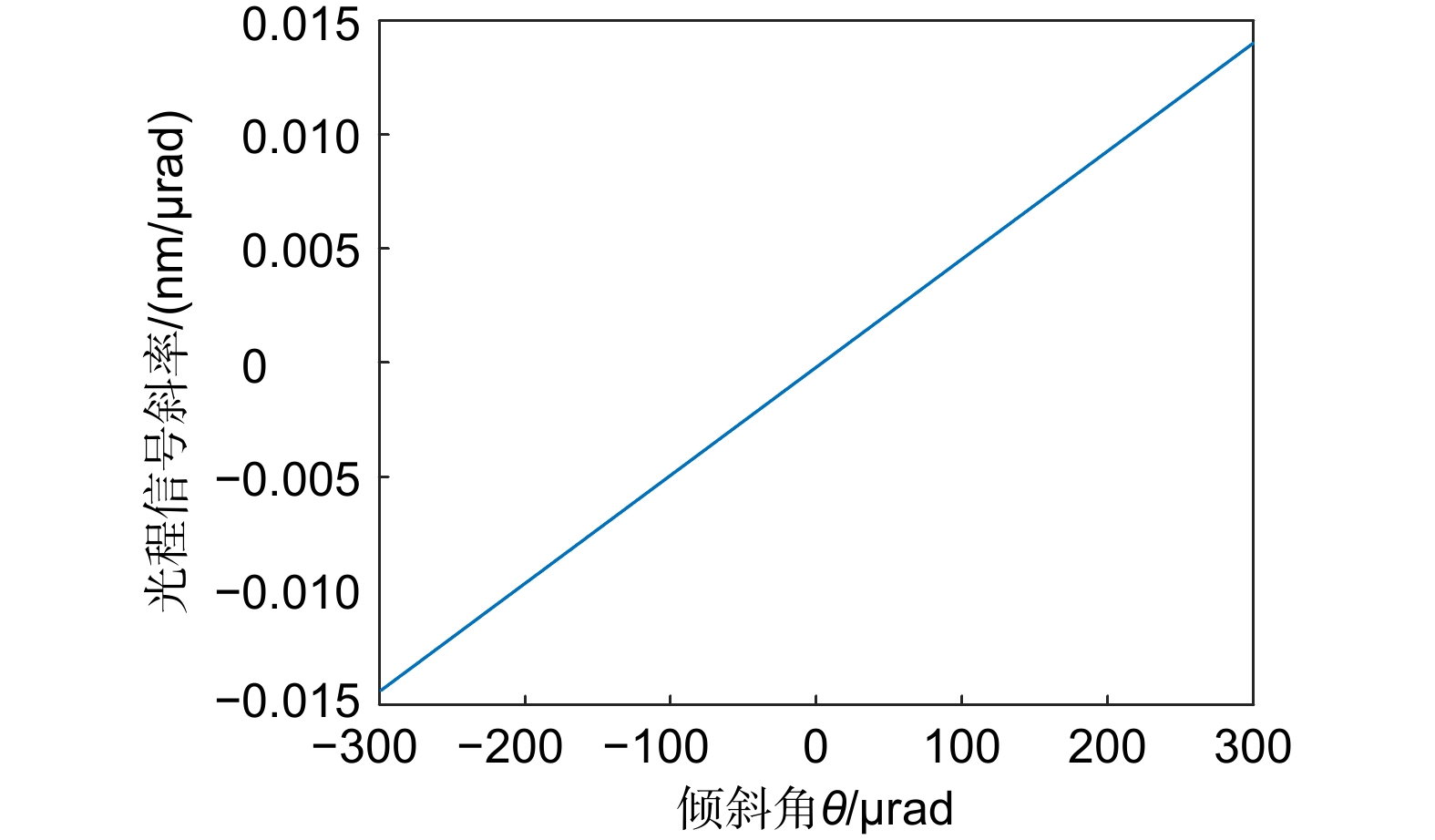
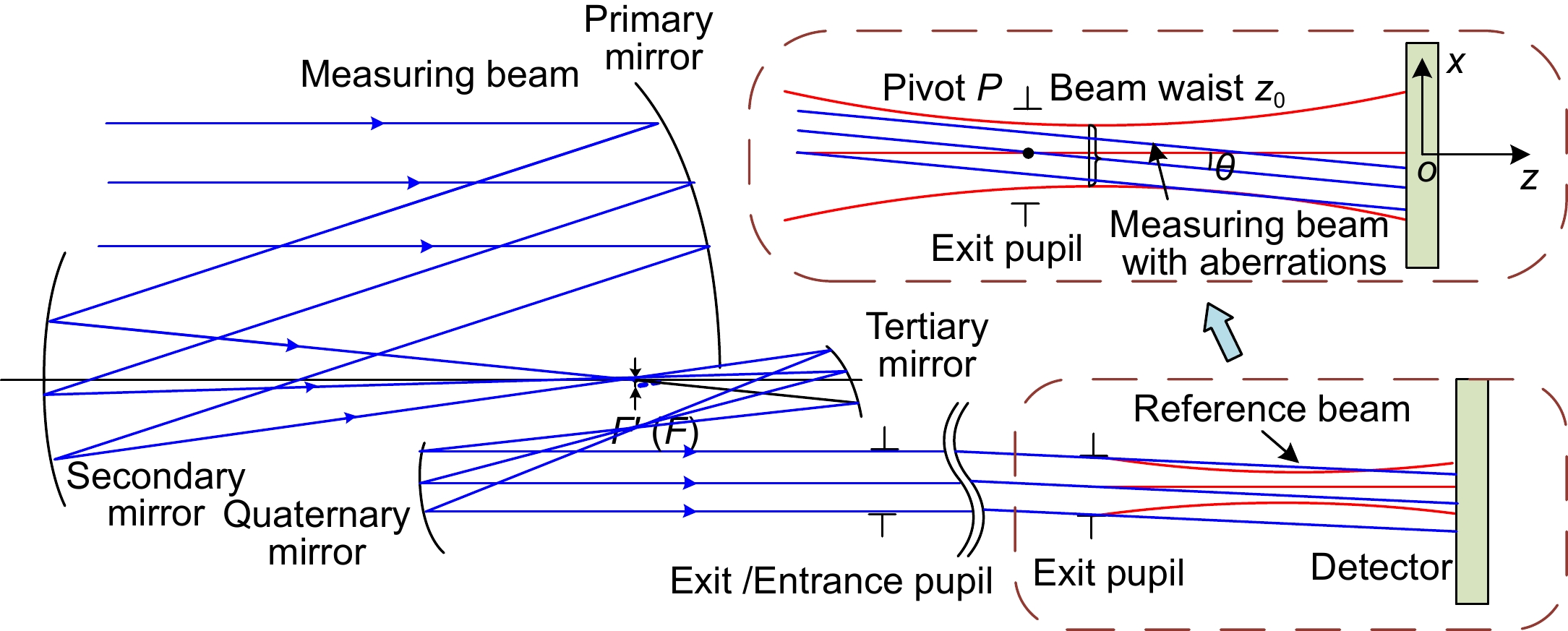
Overview: The TianQin project is a planned space-based gravitational wave observatory in China, consisting of a formation of three spacecraft, each equipped with two telescopes for laser beam transmission and reception. The TianQin mission utilizes heterodyne interferometry to achieve precise distance measurements between test masses. The optical telescopes transmit measurement beams between the spacecraft, forming the long arms of the heterodyne interferometer. Due to the distinct objectives, the telescope system design for the space-based gravitational-wave observatory have slightly different design criteria compared to ordinary telescopes. In addition to meeting the requirements for diffraction-limited imaging quality, maintaining optical path stability is crucial. Wavefront aberrations caused by the telescopes and angular misalignment due to field of view jitter introduce changes in the optical path signal, inevitably generating tilt-to-length coupling noise. Relevant research indicates that the coordinate offset of the chief rays on the pupil plane will cause the TTL noise to exceed the expected level in the interferometer measurement system. While rarely mentioned in conventional optical systems, this system evidently provides a typical application for pupil aberrations. Specifically, the pupil aberration is the preferred option for evaluating telescope aberrations, understanding the requirements for optical path stability, and suppressing tilt-to-length coupling noise. Based on the theory of traditional imaging aberration and pupil aberration theory, the initial structure of the telescope is established, and the automatic correction of pupil aberration and image plane aberration is achieved through macro programming in the commercial optical software Zemax, enabling the design of a high-performance spaceborne telescope. The design results show that the pupil aberration of the system has been corrected, the RMS wavefront error of the scientific field of view is less than λ/200. The maximum value of tilt-to-length coupling noise within a ±300 μrad field of view is 0.0144 nm/µrad, meeting the requirements of the Tianqin mission. The introduction of the concept of pupil aberrations has led to a rapid convergence of TTL noise, clearly providing designers with a new perspective to address the original design issue. Moreover, the pupil aberration evaluation metrics mentioned in this paper can offer an alternative optimization target for other systems requiring pupil aberration correction. This could potentially evolve into a conventional tool in optical design in the future. We believe that our design approach can provide valuable guidance for other space-based gravitational wave detection projects and the design of similar optical systems for space telescopes.
-
-
图 1 发射高斯光束的夫琅禾费衍射模型
Figure 1. Fraunhofer's diffraction model for transmitting Gaussian beam
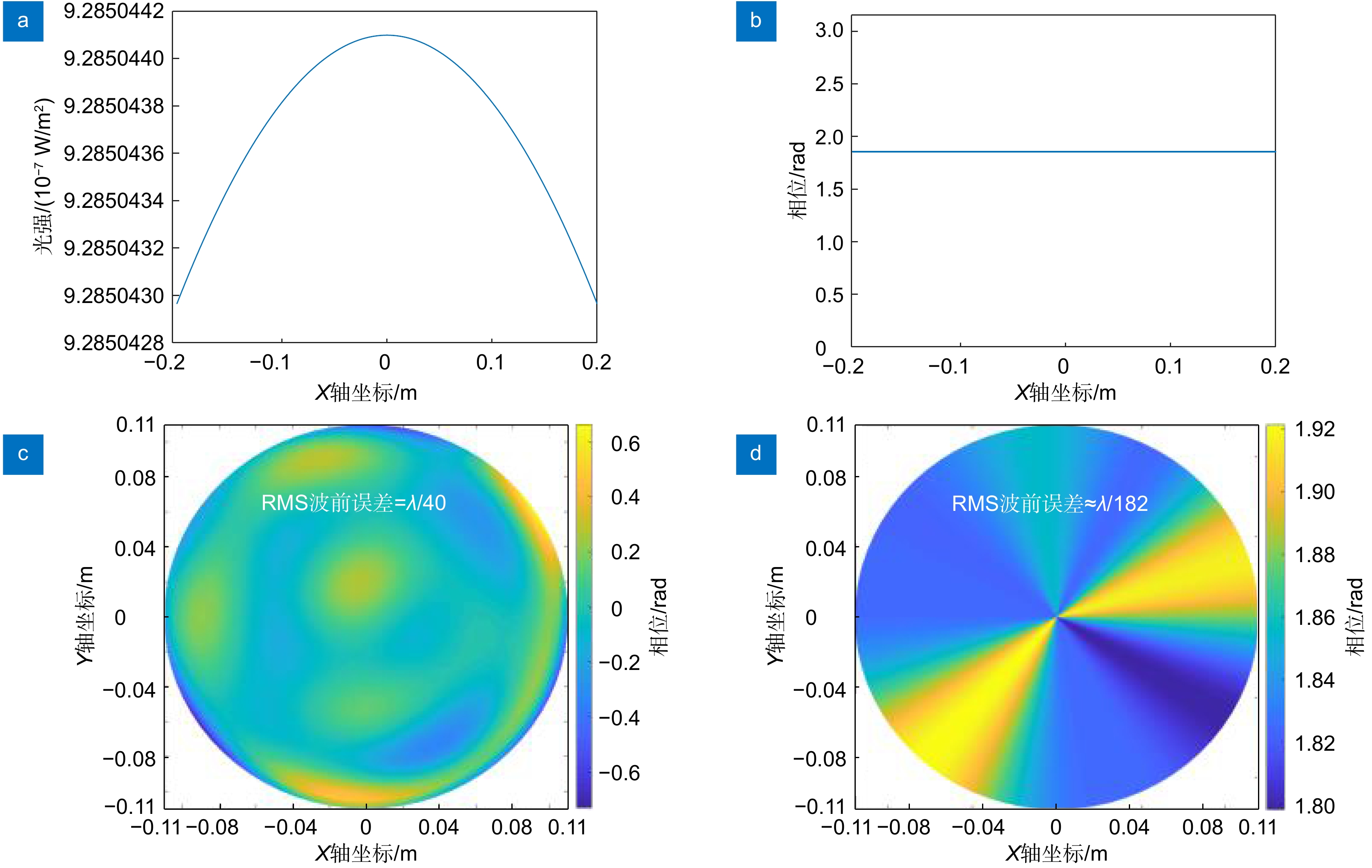
图 2 远场波前。(a)衍射强度分布 ；(b)衍射相位分布； (c)生成的λ/40波前误差；(d)带有λ/40波前误差的远场相位分布
Figure 2. Far-field wavefront. (a) The diffraction intensity distribution; (b) The diffraction phase distribution; (c) The generated phase with wavefront error of λ/40; (d) The diffraction phase distribution of the far field with wavefront error
图 4 光瞳成像过程中主光线和边缘光线的作用
Figure 4. Function of the chief ray and marginal ray in pupil imaging
图 5 初始结构的近轴光线追迹示意图
Figure 5. Schematic diagram of paraxial ray tracing of the initial design
表 1 天琴望远镜的光学指标
Table 1. Specifications of the TianQin telescope
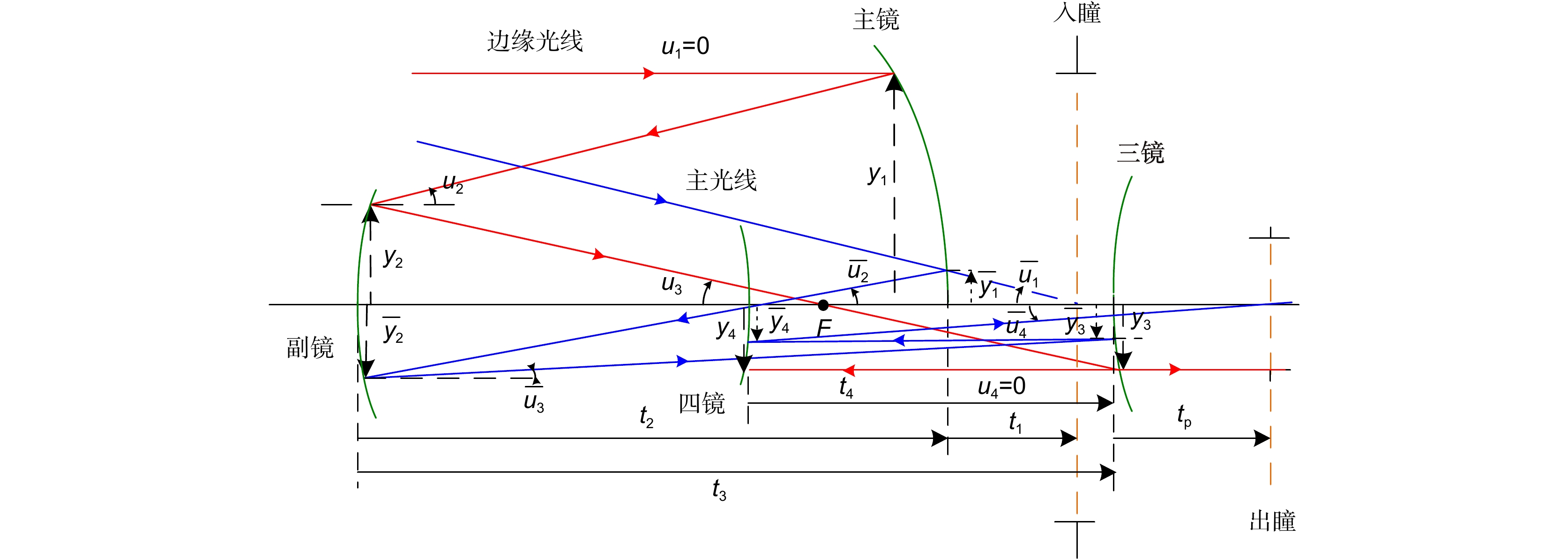
系统参数 设计需求 波长 1064 nm 波前质量(设计残余像差) $ \le \mathrm{\lambda } $/300 RMS@1064 nm 捕获视场 ±200 µrad 科学视场 ±7 µrad 入瞳直径 220 mm 放大倍率 40× 背向杂散光功率 <10−10 of laser power 光程稳定性 TTL≤0.025 nm/μrad 
下载: 导出CSV
表 2 天琴望远镜的同轴初始结构设计参数
Table 2. Coaxial initial structure parameters of the TianQin telescope
表面 曲率半径/mm 厚度/mm 圆锥系数 主镜 −643.455 −300 −0.929 次镜 −47.498 350 − 三镜 −188.985 −60 − 四镜 Infinity − − 像面 − − −
下载: 导出CSV
表 3 离轴结构设计参数
Table 3. Fundamental parameters of final off-axial structures
表面 半径/mm 厚度/mm 圆锥系数 Y偏心/mm X倾斜/(°) 尺寸/mm 主镜 −708.33 −320.02 −0.95 −180 − 230 次镜 −75.09 382.38 −5.41 − − 55 三镜 −195.52 −19.17 16.33 0.09 −8.1 2.5 四镜 49.017 − 18.27 −7.73 −5.5 9.1 像面 − − − − − −
下载: 导出CSV
表 4 离轴结构中的偶次非球面系数
Table 4. Even-order aspheric coefficients of final off-axial structures
表面 四阶项 六阶项 八阶项 十阶项 副镜 −1.31E−06 4.63E−10 −1.74E−13 3.73E−17 三镜 5.34E−03 3.05E−03 −3.875E−03 −1.59E−03 四镜 −5.68E−05 −5.64E−05 −4.019E−08 2.31E−10
下载: 导出CSV
表 5 波前误差Zernike Fringe展开式
Table 5. Wavefront error in the form of Zernike Fringe series expansion
序数 系数ai 多项式Zi 序数 系数 多项式 Z1 −0.0046 1 Z20 0.001969 (5ρ2 − 4) ρ3 sin3θ Z2 0.005705 ρ cosθ Z21 0.001095 (15ρ4 − 20ρ2 + 6) ρ2 cos2θ Z3 −0.01953 ρ sinθ Z22 −3.44E−06 (15ρ4 − 20ρ2 + 6) ρ2 sin2θ Z4 0.008356 2ρ2 − 1 Z23 7.57E−07 (35ρ6 − 60ρ4 + 30ρ2 − 4) ρ cosθ Z5 0.049601 ρ2 cos2θ Z24 −0.0003 (35ρ6 − 60ρ4 + 30ρ2 − 4) ρ sinθ Z6 −0.01931 ρ2 sin2θ Z25 −2.57E−05 70ρ8 − 140ρ6 + 90ρ4 − 20ρ2 + 1 Z7 0.010996 (3ρ2 − 2) cosθ Z26 0.000114 ρ5 cos5θ Z8 0.021988 (3ρ2 − 2) sinθ Z27 −0.00054 ρ5 sin5θ Z9 0.001957 6ρ4 − 6ρ2 + 1 Z28 −0.0001 (6ρ2−5) ρ4 cos5θ Z10 0.022299 ρ3 cos3θ Z29 −1.46E−05 (6ρ2−5) ρ4 sin5θ Z11 0.016406 ρ3 sin3θ Z30 −2.73E−07 (21ρ4 − 30ρ2 + 10) ρ3 cos3θ Z12 −0.00045 (4ρ2 − 3) ρ2 cos2θ Z31 5.70E−05 (21ρ4 − 30ρ2 + 10) ρ3 sin3θ Z13 0.003273 (4ρ2 − 3) ρ2 sin2θ Z32 2.04E−05 (56ρ6 − 105ρ4 + 60ρ2 − 10) ρ2 cos2θ Z14 0.0000082 (10ρ4 − 12ρ2 + 3) ρ cosθ Z33 2.02E−07 (56ρ6 − 105ρ4 + 60ρ2 − 10) ρ2 sin2θ Z15 −0.00074 (10ρ4 − 12ρ2 + 3) ρ sinθ Z34 −5.12E−10 (126ρ8 − 280ρ6 + 210ρ4 − 60ρ2 + 5) ρ cosθ Z16 −0.0006 20ρ6 − 30ρ4 + 12ρ2 − 1 Z35 −4.72E−06 (126ρ8−280ρ6+210ρ4−60ρ2+5) ρ sinθ Z17 −0.00513 ρ4 cos4θ Z36 −3.21E−07 (252ρ10 − 630ρ8 − 560ρ6 − 210ρ4 + 30ρ2 − 1) Z18 −0.00135 ρ4 sin4θ Z37 2.29E−08 924ρ12 − 2772ρ10 + 3150ρ8 − …
1680ρ6 + 420ρ4 − 42ρ2 + 1Z19 0.000825 (5ρ2 − 4) ρ3 cos3θ
下载: 导出CSV
-
参考文献
[1] Abbott B P, Abbott R, Abbott T D, et al. Observation of gravitational waves from a binary black hole merger[J]. Phys Rev Lett, 2016, 116(6): 061102. doi: 10.1103/PhysRevLett.116.061102
[2] Acernese F, Agathos M, Agatsuma K, et al. Advanced Virgo: a second-generation interferometric gravitational wave detector[J]. Class Quantum Gravity, 2015, 32(2): 024001. doi: 10.1088/0264-9381/32/2/024001
[3] Wanner G. Complex optical systems in space: numerical modelling of the heterodyne interferometry of LISA Pathfinder and LISA[D]. Hannover: Leibniz University Hannover, 2010: 1–106.
[4] Danzmann K. LISA mission overview[J]. Adv Space Res, 2000, 25(6): 1129−1136. doi: 10.1016/S0273-1177(99)00973-4
[5] Cornelisse J W. Lisa mission and system design[J]. Class Quantum Gravity, 1996, 13(11A): A251−A258. doi: 10.1088/0264-9381/13/11A/034
[6] Kawamura S, Ando M, Seto N, et al. Current status of space gravitational wave antenna DECIGO and B-DECIGO[J]. Prog Theor Exp Phys, 2021, 2021(5): 05A105. doi: 10.1093/ptep/ptab019
[7] Luo J, Chen L S, Duan H Z, et al. TianQin: a space-borne gravitational wave detector[J]. Class Quantum Gravity, 2016, 33(3): 035010. doi: 10.1088/0264-9381/33/3/035010
[8] Luo Z R, Wang Y, Wu Y L, et al. The Taiji program: a concise overview[J]. Prog Theor Exp Phys, 2021, 2021(5): 05A108. doi: 10.1093/ptep/ptaa083
[9] Schuster S, Wanner G, Tröbs M, et al. Vanishing tilt-to-length coupling for a singular case in two-beam laser interferometers with Gaussian beams[J]. Appl Opt, 2015, 54(5): 1010−1014. doi: 10.1364/AO.54.001010
[10] Wanner G, Heinzel G, Kochkina E, et al. Methods for simulating the readout of lengths and angles in laser interferometers with Gaussian beams[J]. Opt Commun, 2012, 285(24): 4831−4839. doi: 10.1016/j.optcom.2012.07.123
[11] Schuster S, Tröbs M, Wanner G, et al. Experimental demonstration of reduced tilt-to-length coupling by a two-lens imaging system[J]. Opt Express, 2016, 24(10): 10466−10475. doi: 10.1364/OE.24.010466
[12] Sasso C P, Mana G, Mottini S. The LISA interferometer: impact of stray light on the phase of the heterodyne signal[J]. Class Quantum Gravity, 2019, 36(7): 075015. doi: 10.1088/1361-6382/ab0a15
[13] Spector A, Mueller G. Back-reflection from a Cassegrain telescope for space-based interferometric gravitational-wave detectors[J]. Class Quantum Gravity, 2012, 29(20): 205005. doi: 10.1088/0264-9381/29/20/205005
[14] Sankar S R, Livas J. Optical alignment and wavefront error demonstration of a prototype LISA telescope[J]. Class Quantum Gravity, 2020, 37(6): 065005. doi: 10.1088/1361-6382/ab6adf
[15] Livas J C, Arsenovic P, Crow J A, et al. Telescopes for space-based gravitational wave missions[J]. Opt Eng, 2013, 52(9): 091811. doi: 10.1117/1.OE.52.9.091811
[16] Mi Z X, Li Z X, Zhang X D. Construction of a compact off-axis three-mirror reflective system[J]. Appl Opt, 2022, 61(9): 2424−2431. doi: 10.1364/AO.450953
[17] Xu S, Cui Z, Qi B. Compensation factors for 3rd order coma in three mirror anastigmatic (TMA) telescopes[J]. Opt Express, 2018, 26(1): 298−310. doi: 10.1364/OE.26.000298
[18] Ji H R, Zhu Z B, Tan H, et al. Design of a high-throughput telescope based on scanning an off-axis three-mirror anastigmat system[J]. Appl Opt, 2021, 60(10): 2817−2823. doi: 10.1364/AO.421998
[19] Sankar S R, Livas J C. Optical telescope design for a space-based gravitational-wave mission[J]. Proc SPIE, 2014, 9143: 914314. doi: 10.1117/12.2056824
[20] 田思恒, 黄永梅, 徐杨杰, 等. 利用离焦光斑的离轴望远镜失调校正方法研究[J]. 光电工程, 2023, 50(7): 230040. doi: 10.12086/oee.2023.230040
Tian S H, Huang Y M, Xu Y J, et al. Study of off-axis telescope misalignment correction method using out-of-focus spot[J]. Opto-Electron Eng, 2023, 50(7): 230040. doi: 10.12086/oee.2023.230040
[21] McNamara P W. Development of optical techniques for space-borne laser interferometric gravitational wave detectors[D]. Glasgow: University of Glasgow, 1998: 1–144.
[22] Kim D, Choi H, Brendel T, et al. Advances in optical engineering for future telescopes[J]. Opto-Electron Adv, 2021, 4(6): 210040. doi: 10.29026/oea.2021.210040
[23] Livas J, Sankar S, West G, et al. eLISA telescope in-field pointing and scattered light study[J]. J Phys Conf Ser, 2017, 840: 012015. doi: 10.1088/1742-6596/840/1/012015
[24] 牛帅旭, 蒋晶, 唐涛, 等. 望远镜中扰动抑制的Youla控制器优化设计[J]. 光电工程, 2020, 47(9): 190547. doi: 10.12086/oee.2020.190547
Niu S X, Jiang J, Tang T, et al. Optimal design of Youla controller for vibration rejection in telescopes[J]. Opto-Electron Eng, 2020, 47(9): 190547. doi: 10.12086/oee.2020.190547
[25] Wang Z, Yu T, Zhao Y, et al. Research on telescope TTL coupling noise in intersatellite laser interferometry[J]. Photonic Sens, 2020, 10(3): 265−274. doi: 10.1007/s13320-019-0574-5
[26] Zhao Y, Shen J, Fang C, et al. Far-field optical path noise coupled with the pointing jitter in the space measurement of gravitational waves[J]. Appl Opt, 2021, 60(2): 438−444. doi: 10.1364/AO.405467
[27] Lehan J P, Howard J M, Li H, et al. Pupil aberrations in the LISA transceiver design[J]. Proc SPIE, 2020, 11479: 114790D. doi: 10.1117/12.2566373
[28] ESA/SRE 2011 LISA assessment study report (Yellow Book)[EB/OL]. (2011−02)[2023−06]. https://sci.esa.int/documents/35005/36499/1567258681608-LISA_YellowBook_ESA-SRE-2011–3_Feb2011.pdf.
[29] Mahajan V N. Strehl ratio for primary aberrations in terms of their aberration variance[J]. J Opt Soc Am, 1983, 73(6): 860−861. doi: 10.1364/JOSA.73.000860
[30] Livas J C, Sankar S R. Optical telescope system-level design considerations for a space-based gravitational wave mission[J]. Proc SPIE, 2016, 9904: 99041K. doi: 10.1117/12.2233249
[31] Chwalla M, Danzmann K, Barranco G F, et al. Design and construction of an optical test bed for LISA imaging systems and tilt-to-length coupling[J]. Class Quantum Gravity, 2016, 33(24): 245015. doi: 10.1088/0264-9381/33/24/245015
[32] Gross H. Handbook of Optical Systems[M]. Weinheim: Wiley-VCH, 2005: 1–49.
[33] Sasián J. Theory of sixth-order wave aberrations[J]. Appl Opt, 2010, 49(16): D69−D95. doi: 10.1364/AO.49.000D69
[34] Fan Z C, Zhao L J, Cao S Y, et al. High performance telescope system design for the TianQin project[J]. Class Quantum Gravity, 2022, 39(19): 195017. doi: 10.1088/1361-6382/ac8b57
[35] Lakshminarayanan V, Fleck A. Zernike polynomials: a guide[J]. J Mod Opt, 2011, 58(7): 545−561. doi: 10.1080/09500340.2011.554896
-
访问统计
点击扫一扫
图(10)
表(5)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
