E-mail Alert
RSS
Spatial mismatch calibration method for simultaneous slightly off-axis digital holographic microscopy system
-
摘要:
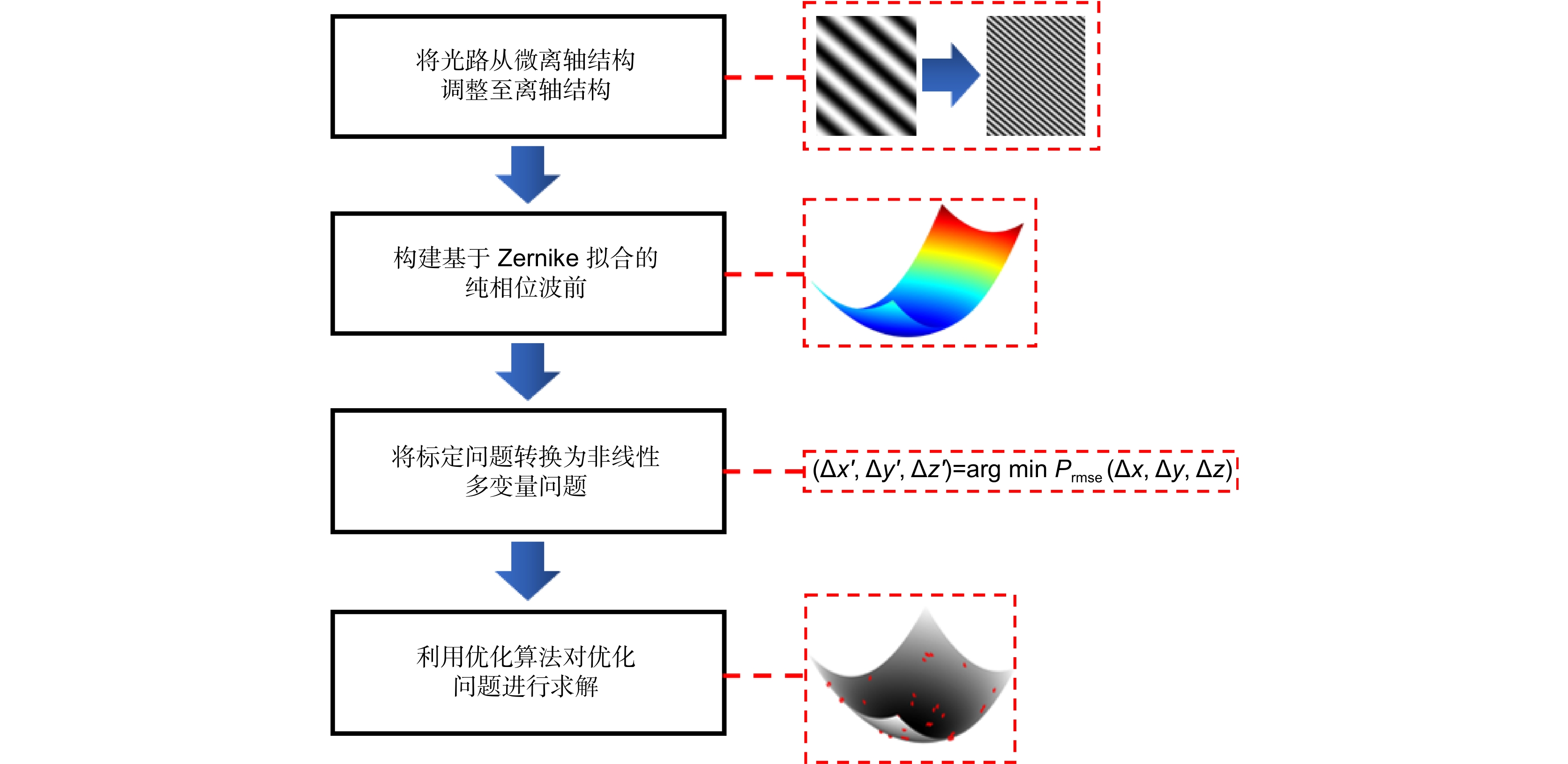
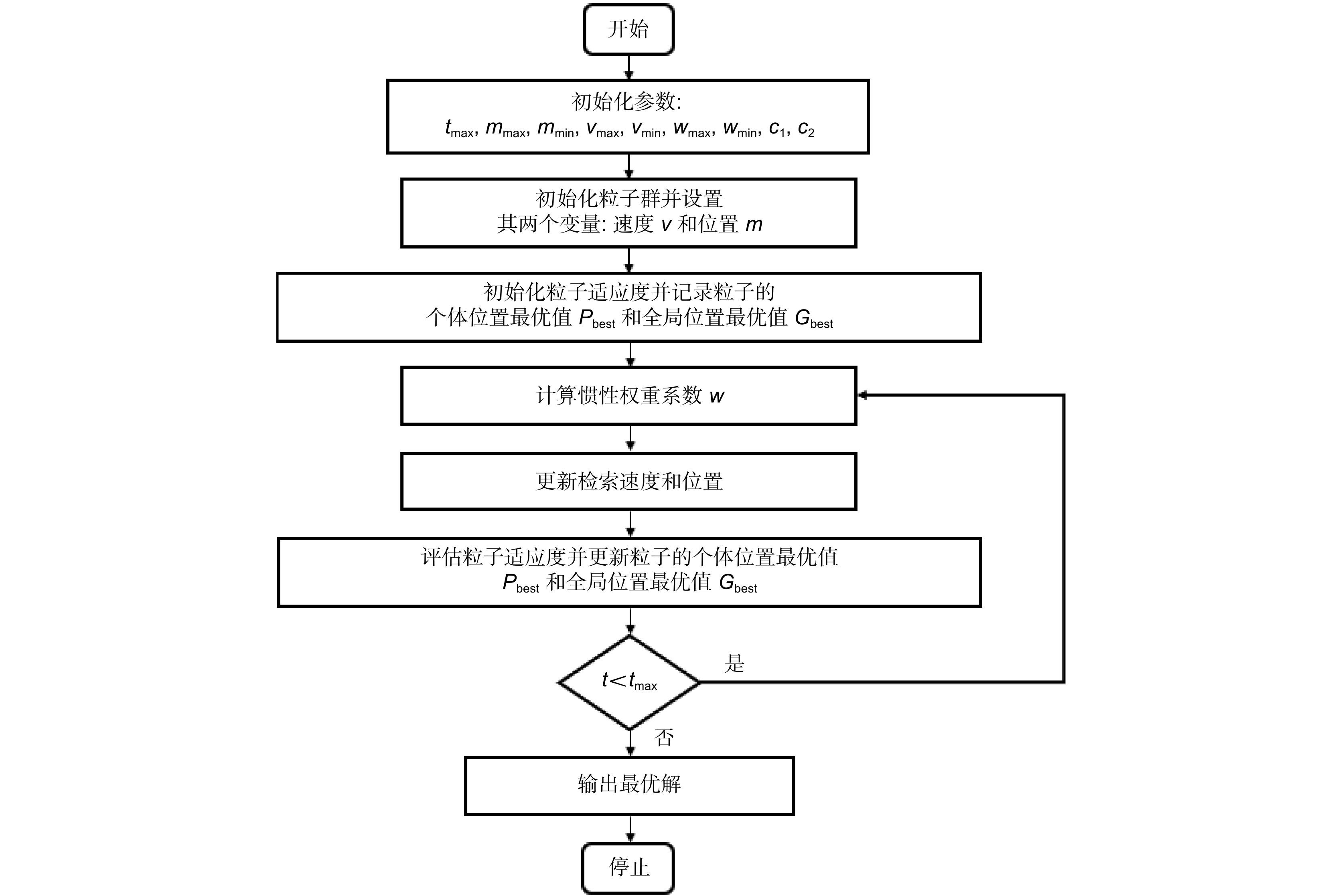
现有的空间失配标定方法受原理限制只能实现像素级的标定精度，且易受环境噪声干扰。本文提出了一种亚像素级的同步微离轴数字全息显微系统的空间失配标定方法。该方法在建模时不仅分析了图像分割导致的横向位置误差，还进一步考虑了传感器倾斜引入的纵向位置误差，并将标定过程归纳为求解非线性多变量优化问题。在本文中，粒子群优化算法因其结构简单、收敛效率高、全局搜索能力强等优势，被用于解决这一优化问题。在标定过程中，建立了基于相位畸变的纯相位波面，并将纯相位波前的均方根误差作为目标函数，以去除噪声对标定精度的影响。仿真结果证明本文方法具有亚像素级精度，实验证明了其在实际系统中的有效性。
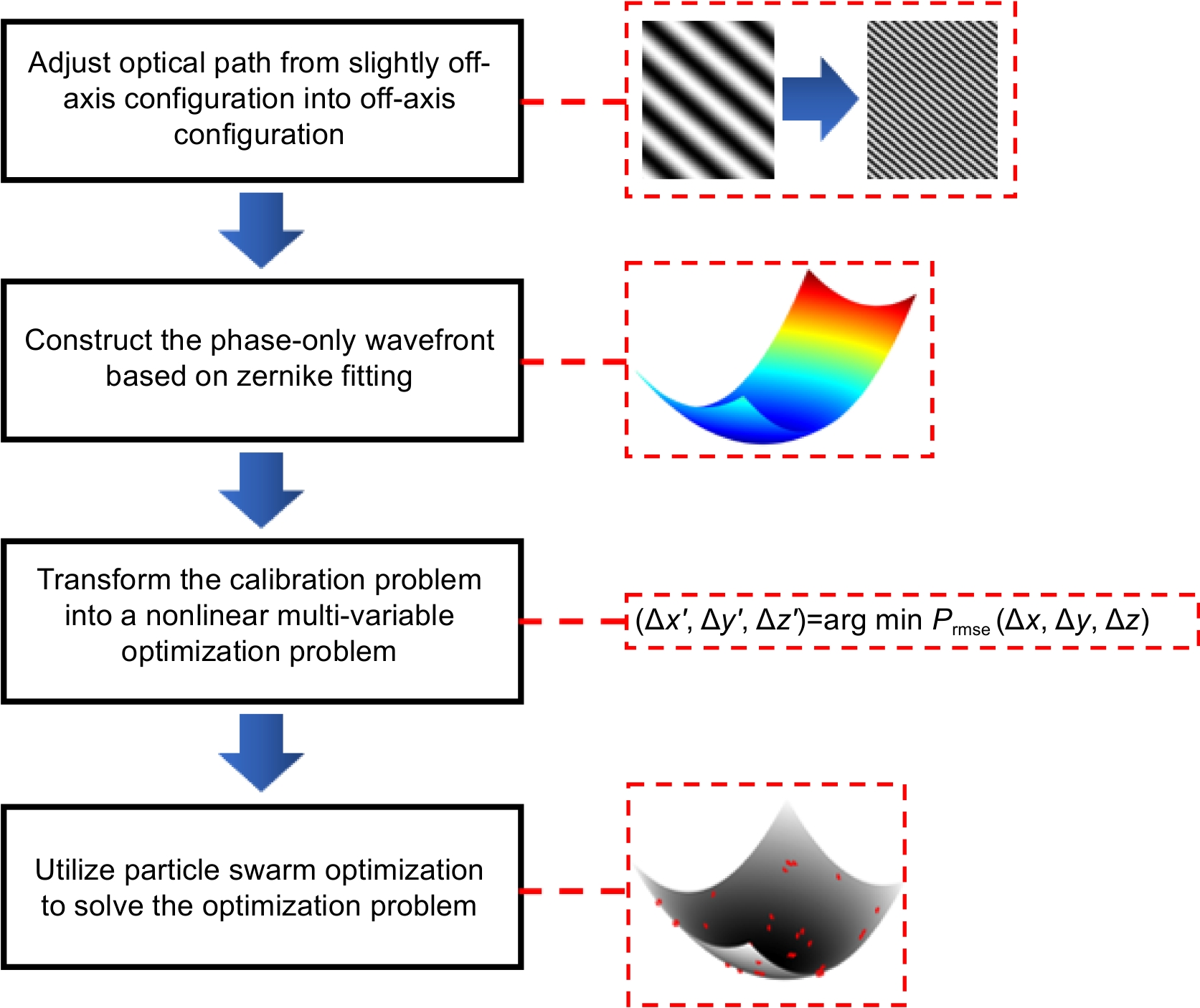
Abstract:The existing spatial mismatch calibration methods can only achieve pixel-level calibration accuracy due to the limitation of principle, and are easily disturbed by the environmental noise. In this paper, a spatial mismatch calibration method for a sub-pixel-level simultaneous slightly off-axis digital holographic microscope system is proposed. In the modeling, the method not only analyzes the lateral position error caused by the image segmentation, but also further considers the longitudinal position error caused by the sensor tilt, and summarizes the calibration process as a nonlinear multi-variable optimization problem. In this paper, the particle swarm optimization algorithm is used to solve this optimization problem because of its simple structure, high convergence efficiency, and strong global search ability. In the calibration process, a phase-only wavefront based on the phase aberration is established, and the root mean square error of the phase-only wavefront is used as the target function to remove the influence of noise on the calibration accuracy. Simulation results show that the proposed method has sub-pixel accuracy, and experiment demonstrates the effectiveness of the method in the practical systems.
-
Overview: With the development of computer and sensor technology, digital holography technology inherited from the traditional optical holography has entered the practical stage. The photo-electric sensor is used to record the hologram formed by the interference of the reference wave and the object wave, and then the complex amplitude of the object wave is recovered in the computer. The advantages of fast, large field of view, non-contact, and high-precision make it a powerful tool in microbial detection, micro-component measurement, particle tracking, and vibration monitoring.
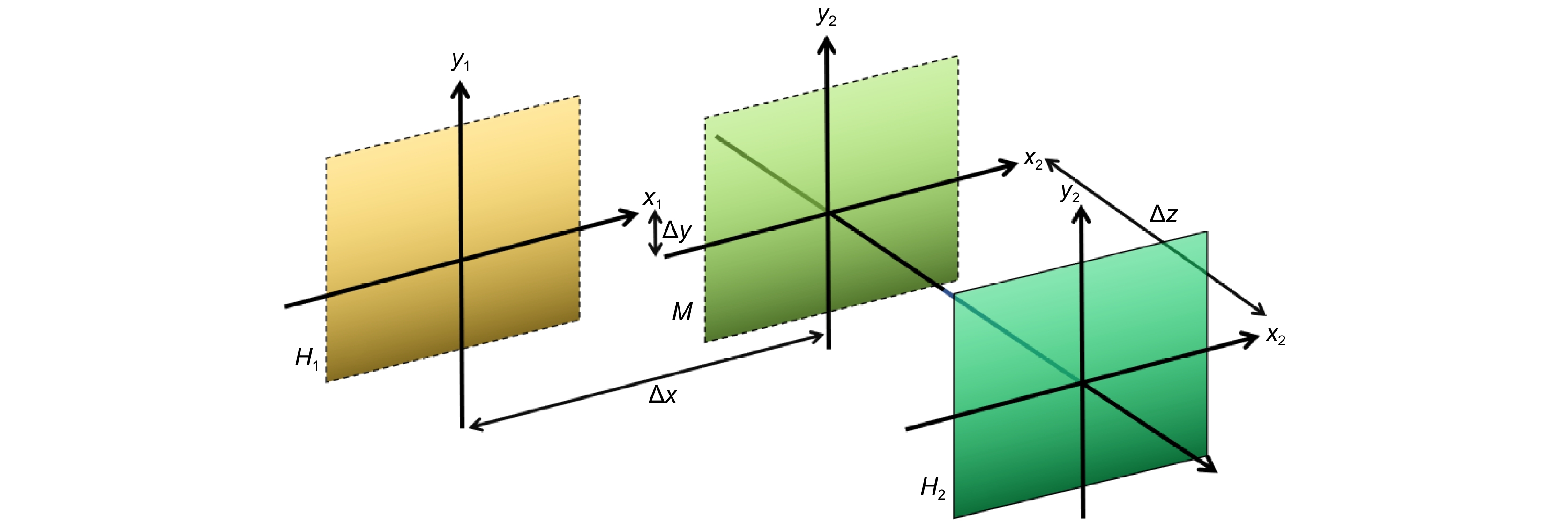
In recent years, slightly off-axis digital holography which combines the advantages of off-axis and on-axis has been vigorously developed. In order to further improve its real-time performance, a synchronous slightly off-axis system based on the field of view (FOV) multiplexing technique has been applied. However, the spatial position of the holograms collected by this technology is unknown, which causes a spatial mismatch problem. In order to ensure the accuracy of the subsequent holographic reconstruction, it is necessary to perform a spatial mismatch calibration. The existing calibration methods can be roughly divided into: intensity-based calibration methods and phase-based calibration methods. Intensity-based calibration methods are susceptible to environmental noise, and phase-based calibration methods only have pixel-level accuracy. At the same time, none of the existing methods take into account the longitudinal position error caused by the sensor tilt.
-
-
图 1 同步微离轴数字全息显微系统光路图
Figure 1. Optical setup of the parallel phase-shifting SODHM system
图 2 空间相对误差的生成原理。 (a) 横向误差；(b) 纵向误差
Figure 2. The generation principle of spatial relative position errors. (a) The longitudinal position error; (b) The transverse position error
图 6 仿真输入。(a) 仿真的相位畸变；(b) 无样本的仿真π/2相移量离轴全息图
Figure 6. Simulation input. (a) Simulated phase aberration; (b) Simulated π/2 phase shifting off-axis holograms without samples
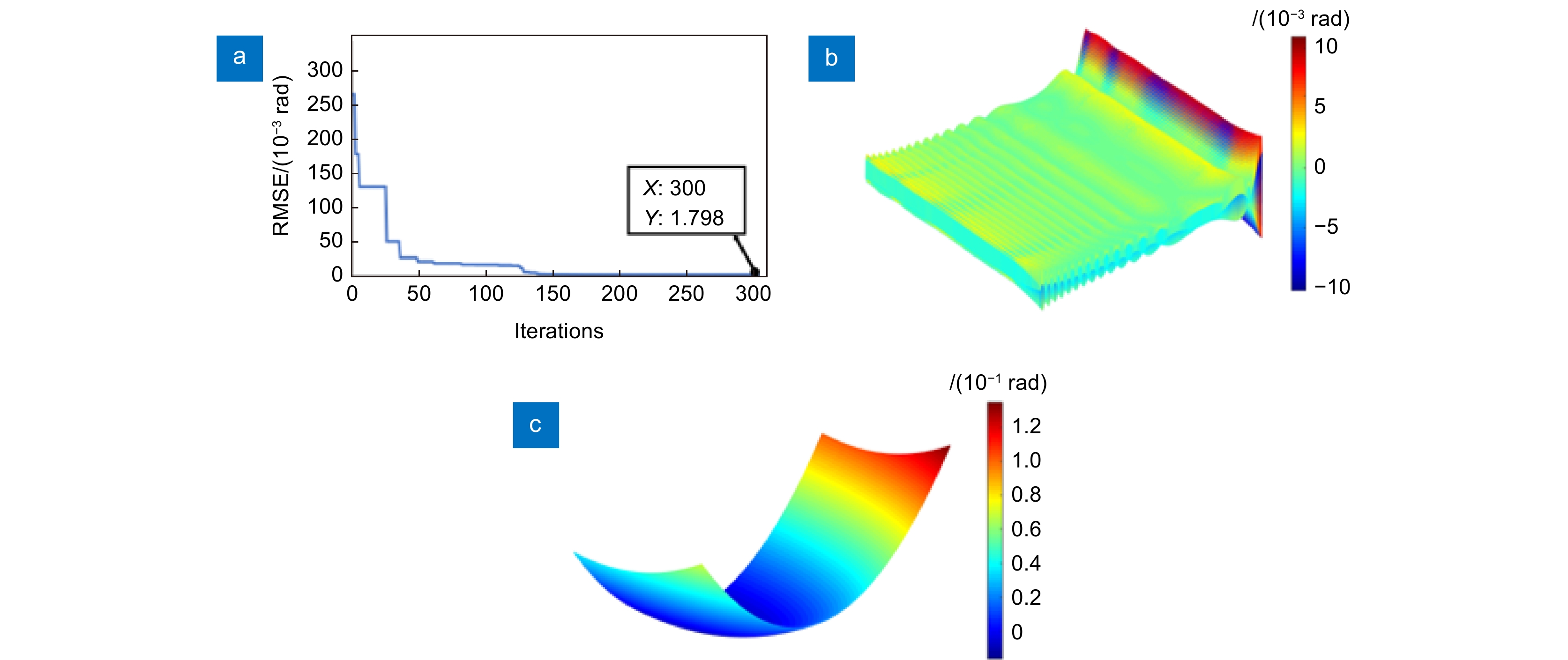
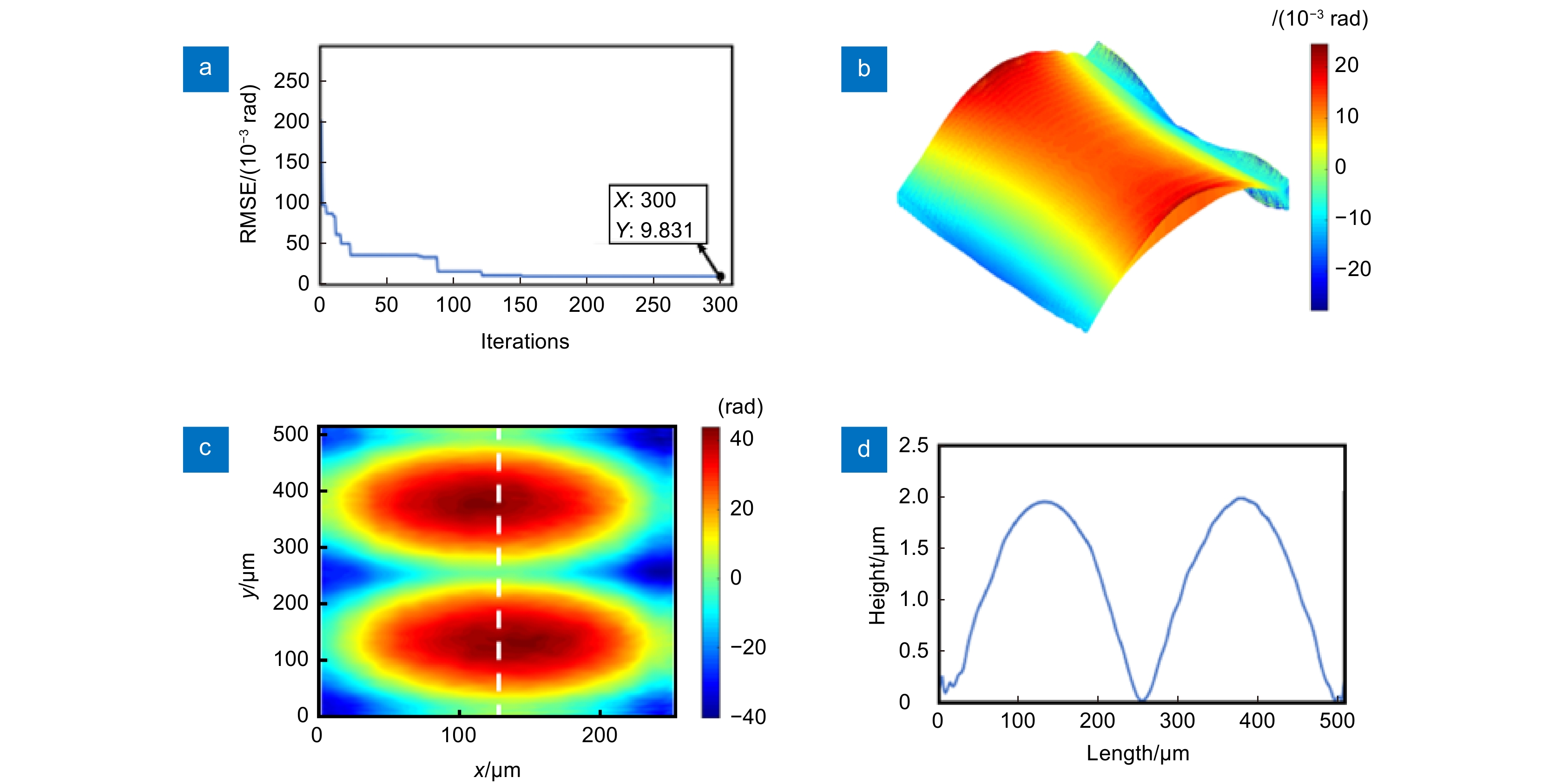
图 7 仿真结果。(a) 基于LDW-PSO的相位分布RMSE收敛曲线； (b) 使用本文方法标定后的整个相位差分布；(c) 使用PPC方法标定后的整个相位差分布
Figure 7. Simulation results. (a) RMSE convergence curve of phase distribution based on LDW-PSO; (b) The whole phase difference distribution after calibration using the method proposed in this paper; (c) The whole phase difference distribution after calibration using PPC method
图 8 实验系统采集的全息图 。(a) 无样品的离轴全息图； (b) 带样品的微离轴全息图
Figure 8. Holograms collected by the experimental system. (a) The off-axis hologram without sample; (b) The slightly off-axis holograms with sample
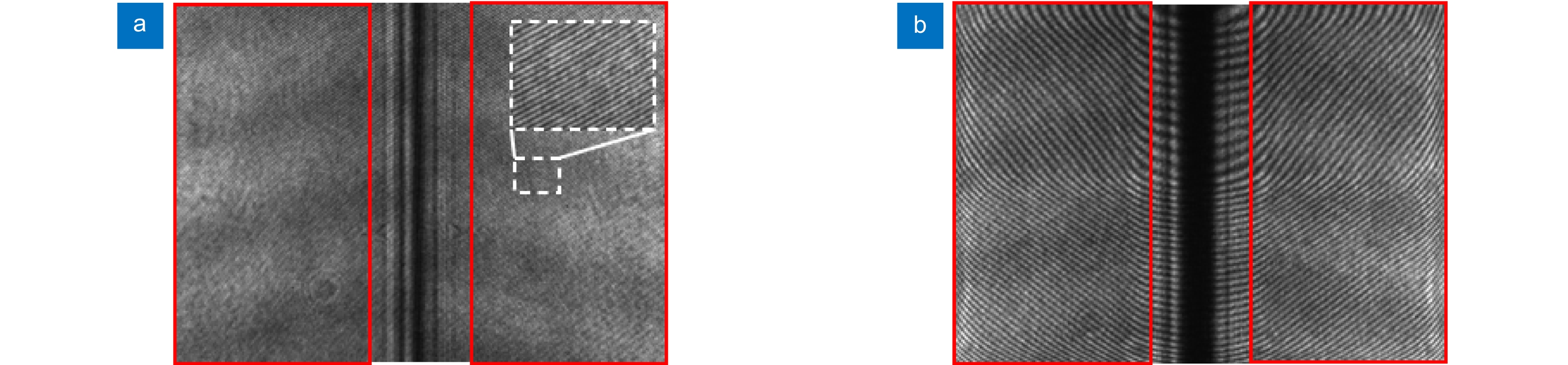
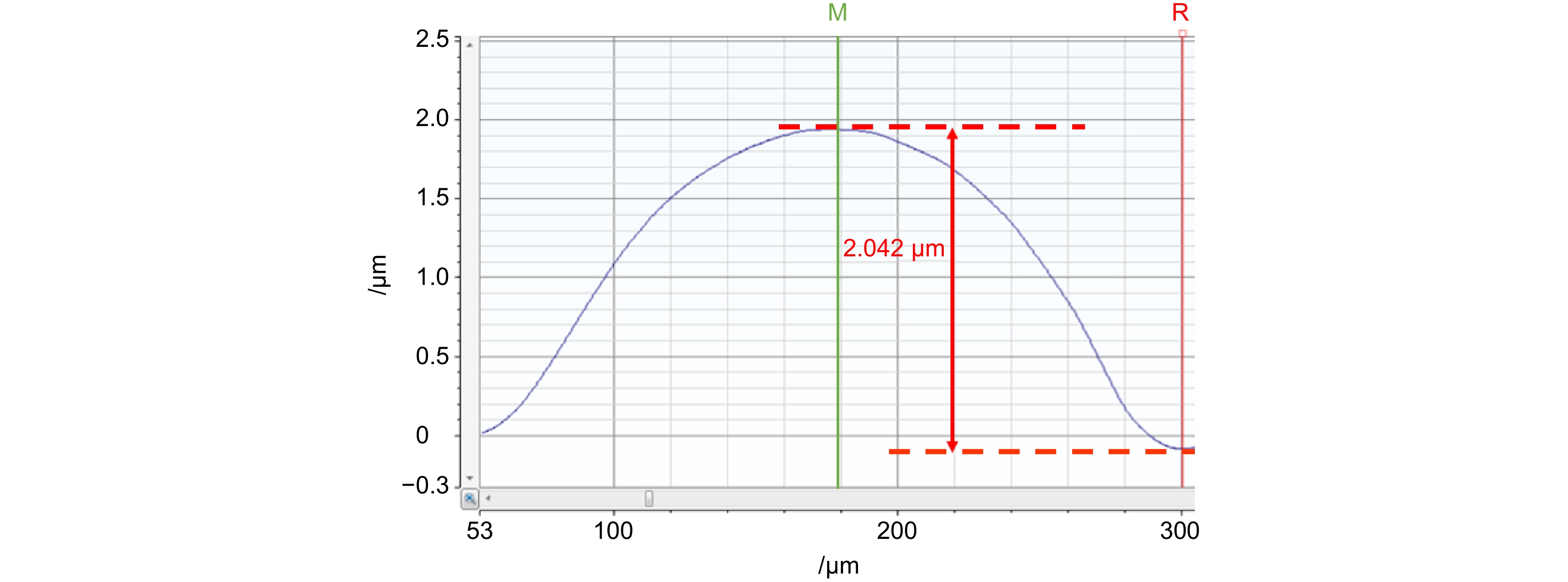
图 10 实验结果。(a) 基于LDW-PSO的相位分布RMSE收敛曲线； (b) 校准后的整个相位差分布；(c) 重建的样本相位分布；(d) 沿着图10(c)中标记的白线的轮廓
Figure 10. Experimental results. (a) The RMSE convergence curve of phase distribution based on LDW-PSO; (b) The entire phase difference distribution after calibration; (c) The phase distribution of reconstructed sample; (d) The outline of the white line marked in Figure 10(c)
表 1 仿真中ZEMAX类型的Zernike多项式及其系数
Table 1. Zernike polynomials of ZEMAX type and their coefficients in the simulation
阶数 多项式 系数 $1 $ $2x$ $ - 9 \times {10^{ - 3}}$ $2 $ $2y$ $600 $ $3 $ $\sqrt 3 (2{x^2} + 2{y^2} - 1)$ $3.6 \times {10^6}$ $4 $ $\sqrt 6 (2xy)$ $0 $ $5 $ $\sqrt 6 ({x^2} - {y^2})$ $1.6 \times {10^6}$ $6 $ $\sqrt 8 (3{x^2}y + 3{y^2} - 2y)$ $0 $ $7 $ $\sqrt 8 (3{x^3} + 3x{y^2} - 2x)$ $0 $ $8 $ $\sqrt 8 (3{x^2}y - {y^3})$ $0 $ $9 $ $\sqrt 8 ({x^3} - 3x{y^2})$ $6.0622 \times {10^6}$ 
下载: 导出CSV
表 2 相对位置误差的数据比较
Table 2. Data comparison of relative position error
$\Delta x/{\rm{pixel}}$ $\Delta y/{\rm{pixel}}$ $\Delta {\textit{z}}/{\rm{mm}}$ 引入的误差 −30.415 25.562 1.300 PPC法标定结果 −30 26 None 本文方法标定结果 −30.410 25.568 1.298
下载: 导出CSV
表 3 相对位置误差的实验数据
Table 3. Experimental data of relative position error
$\Delta x/{\rm{pixel}}$ $\Delta y/{\rm{pixel}}$ $\Delta {\textit{z}}/{\rm{mm}}$ 标定结果 −10.845 1.383 0.813
下载: 导出CSV
-
[1] 田鹏, 严伟, 李凡星, 等. 均匀球面波数字同轴全息生物显微方法[J]. 光电工程, 2019, 46(1): 180110. doi: 10.12086/oee.2019.180110
Tian P, Yan W, Li F X, et al. Biology microscopy using well-distributed sphere digital in-line holography[J]. Opto-Electron Eng, 2019, 46(1): 180110. doi: 10.12086/oee.2019.180110
[2] 李光勇, 杨岩. 数字全息粒子图像测速技术应用于旋转流场测量的研究[J]. 中国激光, 2012, 39(6): 0609001. doi: 10.3788/CJL201239.0609001
Li G Y, Yang Y. Digital holography particle image velocimetry applied for measurement of the rotating flow fields[J]. Chin J Lasers, 2012, 39(6): 0609001. doi: 10.3788/CJL201239.0609001
[3] Cuche E, Marquet P, Depeursinge C. Simultaneous amplitude-contrast and quantitative phase-contrast microscopy by numerical reconstruction of Fresnel off-axis holograms[J]. Appl Opt, 1999, 38(34): 6994−7001. doi: 10.1364/AO.38.006994
[4] 史晓玉, 王大勇, 戎路, 等. 连续太赫兹波数字全息相衬成像[J]. 光电工程, 2020, 47(5): 190543. doi: 10.12086/oee.2020.190543
Shi X Y, Wang D Y, Rong L, et al. Phase contrast imaging based on continuous-wave terahertz digital holography[J]. Opto-Electron Eng, 2020, 47(5): 190543. doi: 10.12086/oee.2020.190543
[5] Vijayakumar A, Katkus T, Lundgaard S, et al. Fresnel incoherent correlation holography with single camera shot[J]. Opto-Electron Adv, 2020, 3(8): 200004. doi: 10.29026/oea.2020.200004
[6] Yamaguchi I, Zhang T. Phase-shifting digital holography[J]. Opt Lett, 1997, 22(16): 1268−1270. doi: 10.1364/OL.22.001268
[7] Cuche E, Marquet P, Depeursinge C. Spatial filtering for zero-order and twin-image elimination in digital off-axis holography[J]. Appl Opt, 2000, 39(23): 4070−4075. doi: 10.1364/AO.39.004070
[8] Shaked N T, Zhu Y Z, Rinehart M T, et al. Two-step-only phase-shifting interferometry with optimized detector bandwidth for microscopy of live cells[J]. Opt Express, 2009, 17(18): 15585−15591. doi: 10.1364/OE.17.015585
[9] Gao P, Yao B L, Harder I, et al. Parallel two-step phase-shifting digital holograph microscopy based on a grating pair[J]. J Opt Soc Am A, 2011, 28(3): 434−440. doi: 10.1364/JOSAA.28.000434
[10] Picazo-Bueno J A, Trusiak M, Micó V. Single-shot slightly off-axis digital holographic microscopy with add-on module based on beamsplitter cube[J]. Opt Express, 2019, 27(4): 5655−5669. doi: 10.1364/OE.27.005655
[11] Shaked N T, Rinehart M T, Wax A. Dual-interference-channel quantitative-phase microscopy of live cell dynamics[J]. Opt Lett, 2009, 34(6): 767−769. doi: 10.1364/OL.34.000767
[12] Kiire T, Nakadate S, Shibuya M. Phase-shifting interferometer based on changing the direction of linear polarization orthogonally[J]. Appl Opt, 2008, 47(21): 3784−3788. doi: 10.1364/AO.47.003784
[13] Millerd J E, Brock N J, Denneau L Jr. Calibration and error correction in multi-channel imaging: 20050083531[P]. 2005-04-21.
[14] Hahn J, Kim H, Lim Y, et al. Spatial phase-shifting interferometry with compensation of geometric errors based on genetic algorithm[J]. Chin Opt Lett, 2009, 7(12): 1113−1116. doi: 10.3788/COL20090712.1113
[15] Li B, Chen L, Zhao B, et al. Spatial mismatch calibration using circular carrier technique in the simultaneous phase shifting interferometry[J]. Appl Opt, 2012, 51(8): 1037−1044. doi: 10.1364/AO.51.001037
[16] Zheng D H, Chen L, Yang Y, et al. Spatial mismatch calibration based on fast partial phase correlation for interferograms in dynamic Fizeau interferometer[J]. Opt Eng, 2020, 59(3): 034104. doi: 10.1117/1.OE.59.3.034104
[17] Bai H Y, Shan M G, Zhong Z, et al. Parallel-quadrature on-axis phase-shifting common-path interferometer using a polarizing beam splitter[J]. Appl Opt, 2015, 54(32): 9513−9517. doi: 10.1364/AO.54.009513
[18] Goodman J W. Introduction to Fourier Optics[M]. 3rd ed. Greenwood Village, USA: Roberts and Company Publishers, 2005.
[19] Yamada I. The hybrid steepest descent method for the variational inequality problem over the intersection of fixed point sets of nonexpansive mappings[J]. Stud Comput Math, 2001, 8: 473−504. doi: 10.1016/S1570-579X(01)80028-8
[20] Yuan K, Ling Q, Yin W T. On the convergence of decentralized gradient descent[J]. SIAM J Optim, 2013, 26(3): 1835−1854. doi: 10.1137/130943170
[21] Dai Y H, Li L Z, Li D. On restart procedures for the conjugate gradient method[J]. Numer Algorithms, 2004, 35(2-4): 249−260. doi: 10.1023/B:NUMA.0000021761.10993.6e
[22] Jamrus T, Chien C F, Gen M, et al. Hybrid particle swarm optimization combined with genetic operators for flexible job-shop scheduling under uncertain processing time for semiconductor manufacturing[J]. IEEE Trans Semicond Manufact, 2018, 31(1): 32−41. doi: 10.1109/TSM.2017.2758380
[23] Liu J, Qiu X H. A novel hybrid PSO-BP algorithm for neural network training[C]//International Joint Conference on Computational Sciences and Optimization. Sanya, 2009.
[24] Li M Q, Lin D, Kou J S. A hybrid niching PSO enhanced with recombination-replacement crowding strategy for multimodal function optimization[J]. Appl Soft Compu, 2012, 12(3): 975−987. doi: 10.1016/j.asoc.2011.11.032
[25] Bansal J C, Singh P K, Saraswat M, et al. Inertia weight strategies in particle swarm optimization[C]//Third World Congress on Nature and Biologically Inspired Computing. Salamanca, Spain, 2011.
-
点击扫一扫
图(11)
表(3)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
