E-mail Alert
RSS
Highly confined localized spoof plasmon resonance characteristics on space-filling curvilinear meta-structures
-
摘要:
本文提出了一种基于空间填充曲线的超构表面结构，利用理论分析、数值仿真的方法研究了该超构表面的近场电磁特性，实现了高度局域及高品质因子(Q-factor)的多阶人工局域表面等离激元共振(spoof plasmon resonances)。我们发现采用不同结构形状和尺寸的空间填充曲线均可产生共振频率规则分布的多阶谐振模式，通过调整结构的等效波导长度，可同时获得高的谐振波长/结构尺寸压缩比与高品质因子。空间填充曲线所支持的人工局域表面等离激元由磁偶极子与电偶极子模式交替支持；其余参数不变的情况下改变空间填充曲线的分布形式，结构所支持的表面等离激元的谐振特性不受形状曲折的影响，而只与等效波导总长度有关。此外，近场模式的强度分布随着空气波导的走向而改变，可根据实际需求对结构进行特定排布。本文的研究结果对设计基于空间填充曲线的小型化高品质因子电磁谐振器件具有重要的指导意义。
Abstract:With the advent of the 5G communication era, much attention has been paid to manipulate electromagnetic waves at subwavelength scale. In this paper, we propose comb-shaped meta-structures based on space-filling curves, and use theoretical analysis and numerical simulation method to study the near-field electromagnetic properties of these meta-surfaces. Finally, the effective excitation of all order eigenmodes of spoof localized surface plasmon resonance can be realized in these meta-structures. Through adjusting the structure period to change the effective length of the air waveguide, high compression ratio between resonant wavelength and device size, and high Q-factor can be simultaneously achieved. Moreover, spoof localized surface plasmons excited by space-filling structures are alternately supported by magnetic dipole and electric dipole modes. As a consequence, changing the distribution form of the space-filling curve with the remaining parameters unchanged, the resonant characteristics of the surface plasmon supported by the structure are not affected by the shape tortuosity, but are only related to the total length of the equivalent waveguide. Thus, the space-filling curvilinear structure can be freely designed. We believe that, our results have great potential in designing the high Q-factor miniaturized electromagnetic resonator devices based on spacing-filling curvilinear meta-structure.
-
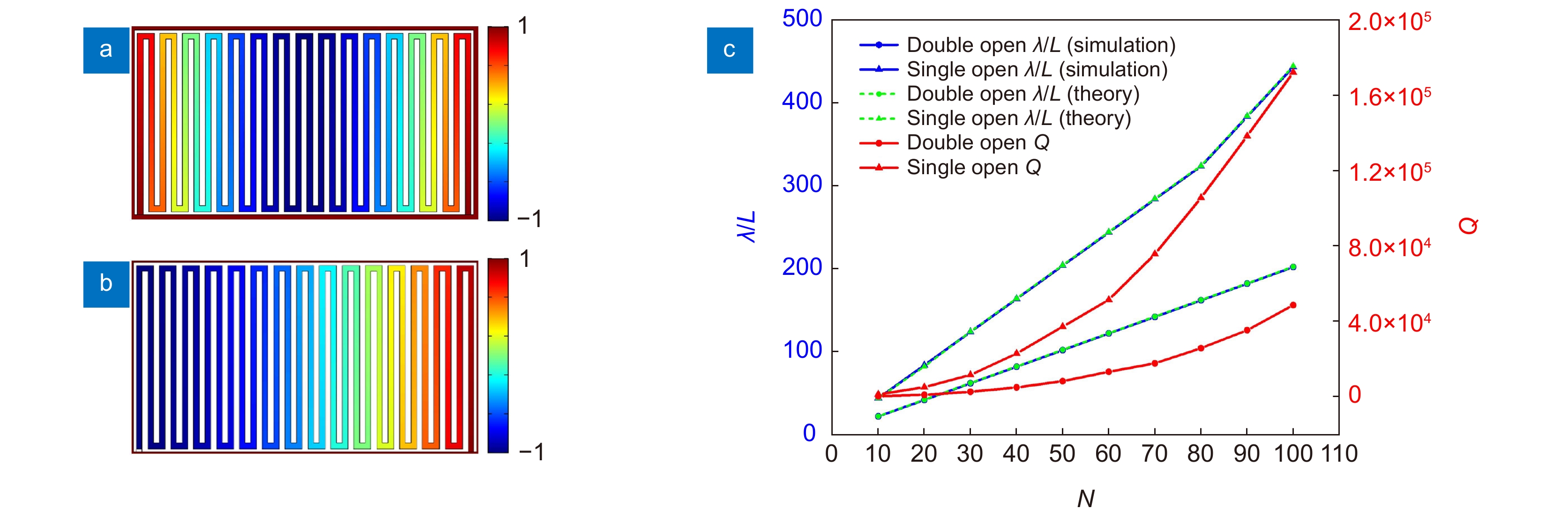
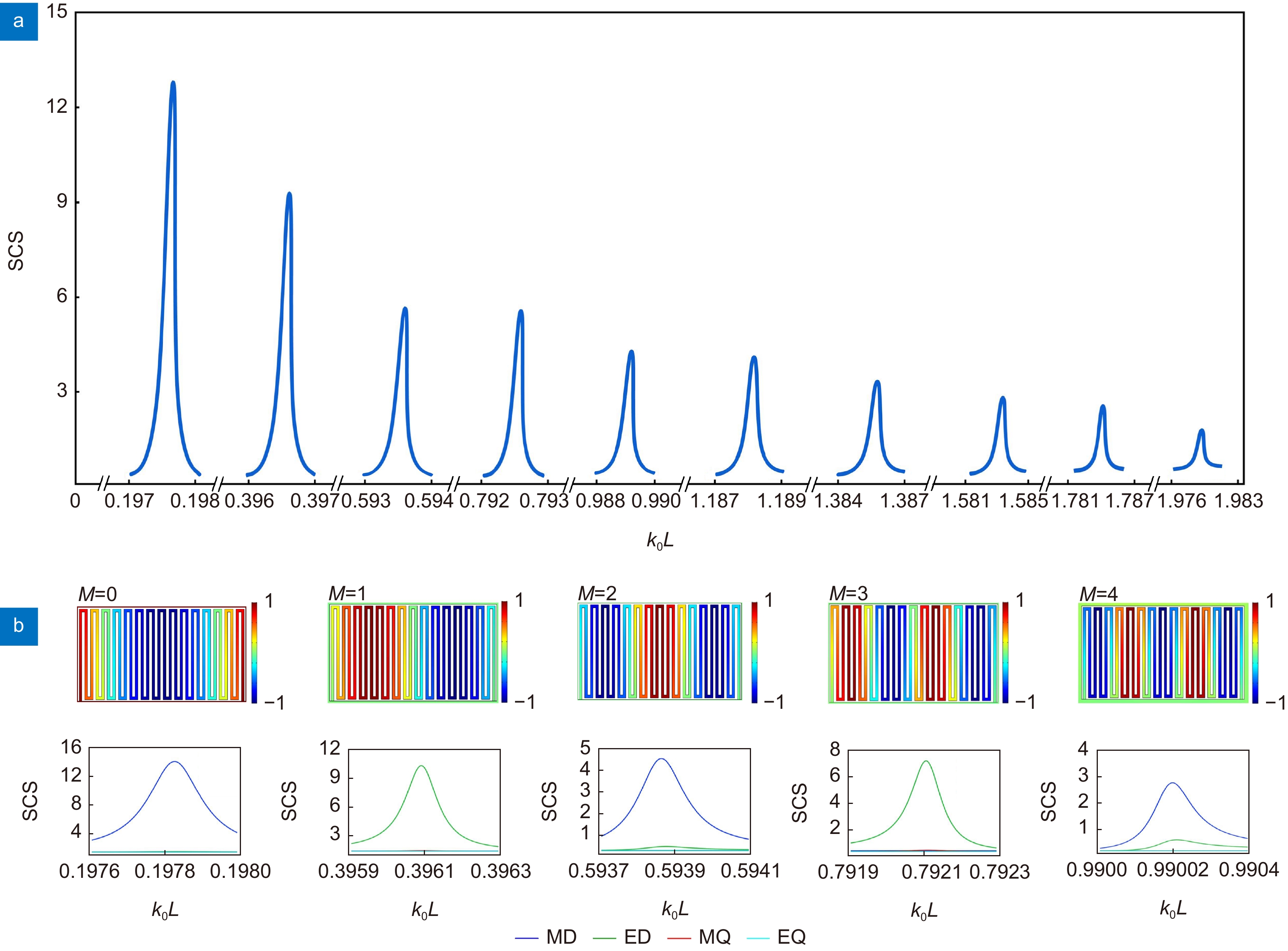
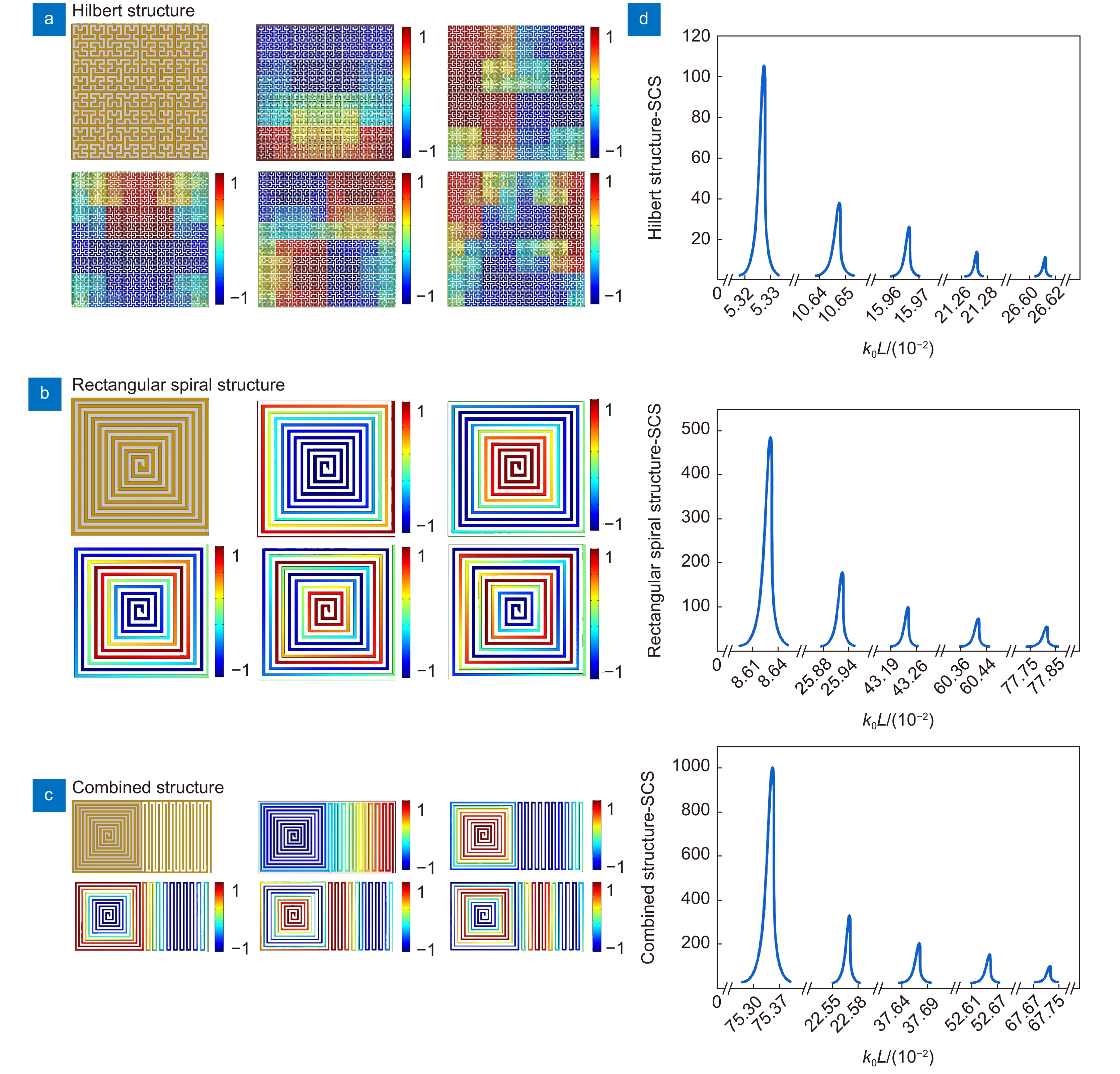
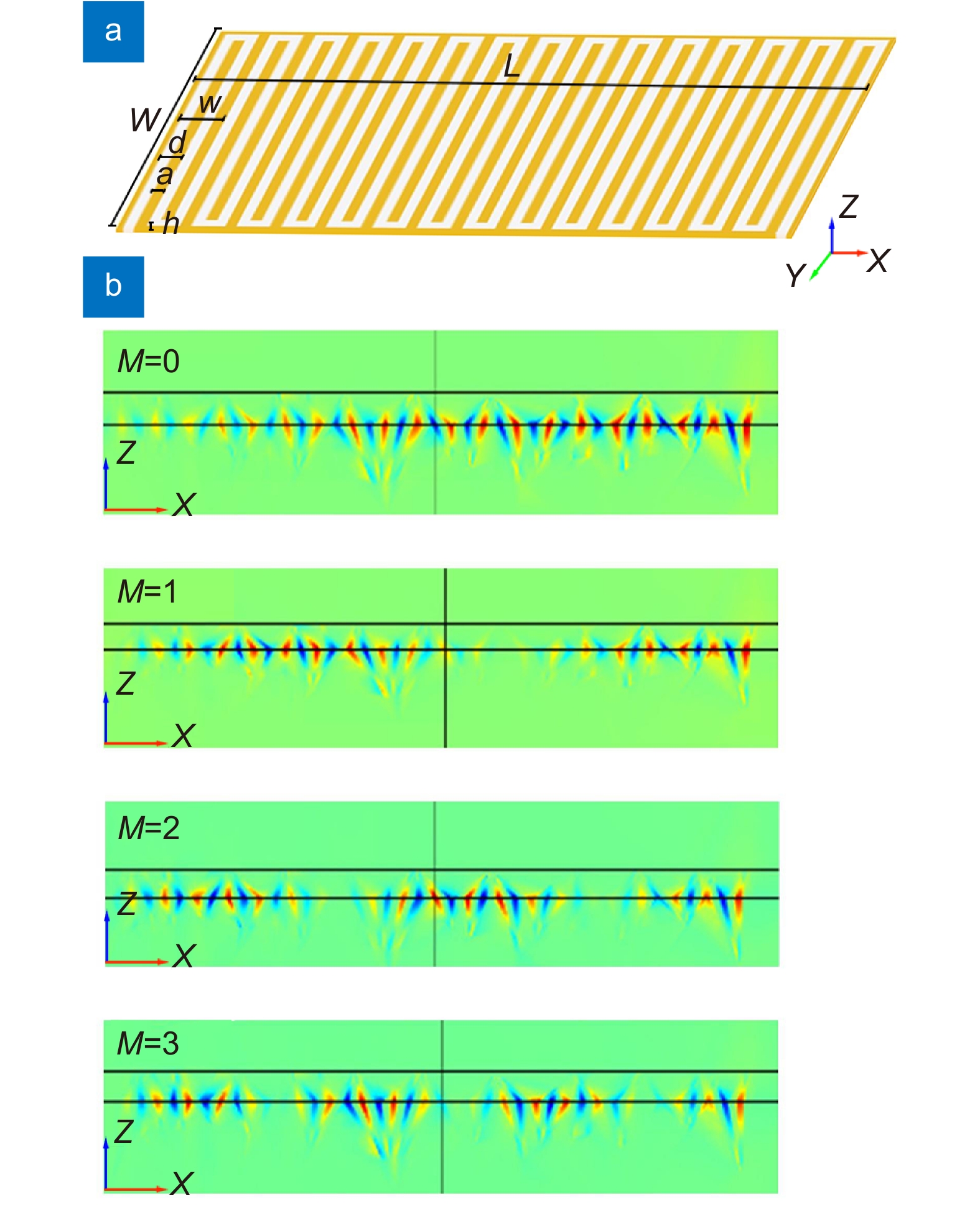
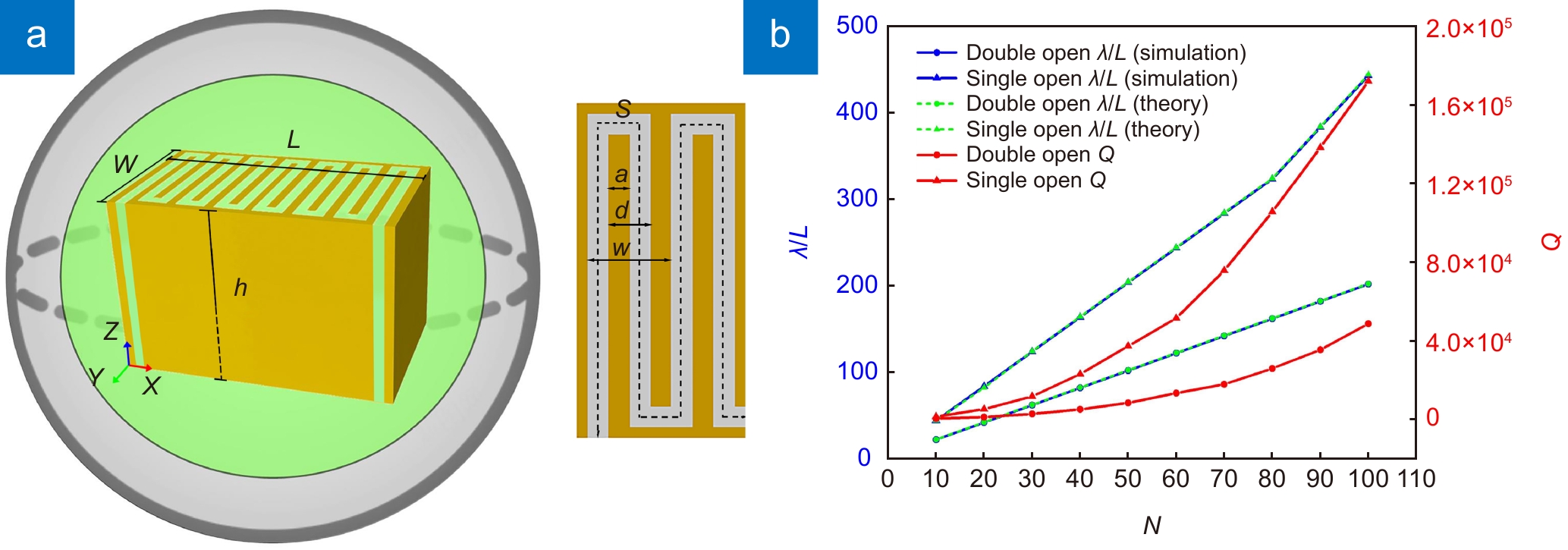
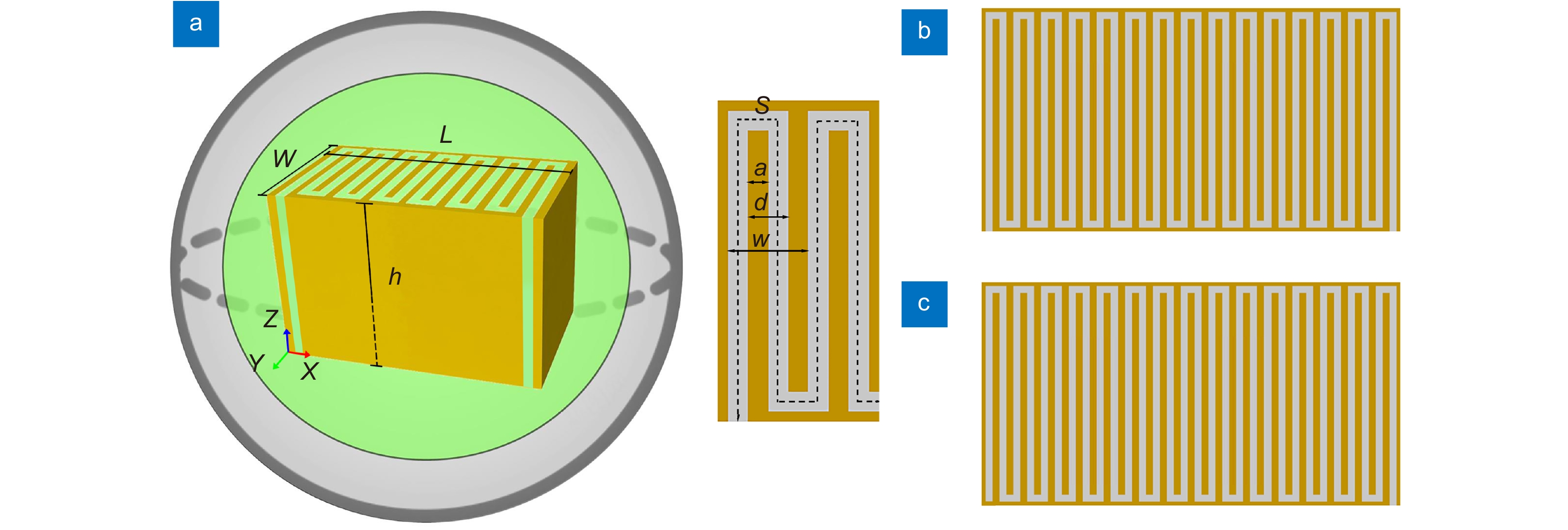
Overview: With the advent of the 5G communication era, much attention has been paid to free manipulate electromagnetic waves at a subwavelength scale. Meta-surface with subwavelength structural dimensions have shown broad prospects in the field of microelectronic components due to their powerful electromagnetic control capabilities. In this paper, a subwavelength comb-shaped space-filling meta-surface is designed by using metal curves according to the resonator principle. A series of studies on spoof localized surface plasmon resonance characteristics are carried out on this basis. Theoretical analysis and calculation are carried out according to the structural characteristics. Compared with the traditional meta-surface supporting spoof localized surface plasmons, this curved arrangement of continuous metals will form an air waveguide similar to a resonant cavity, allowing for larger waveguide lengths at smaller dimensions, resulting in greatly reduced working frequency band. Under the excitation of the incident electromagnetic wave, spoof localized surface plasmon like Fabry-Perot resonance will be generated. The resonance frequency of the meta-surface can be calculated from the resonance conditions. Using the finite element method to simulate the 2D comb structure with different periods, it is found that the Q-factor of 1.7×105 can be obtained when the structure compression ratio (λ/L) is 444 by adjusting the structure period. In the study of the higher-order eigenmodes of the comb-shaped space-filled meta-structure, it was found that the spoof localized surface plasmons excited by space-filling structures are alternately supported by magnetic and electric multipoles modes, and the scattering cross-section of the eigenmodes of each order are presented at equally spaced frequencies. By changing the distribution type of the space-filling structure, the supported surface plasmon resonance properties are not affected by the arbitrary bending of the structure, and the magnetic field intensity distribution of the eigenmodes only changes with the direction of the air waveguide. Finally, the 3D simulation of the comb-shaped space-filling structure is carried out, from the X-Z section electric field diagram, it can be observed that the spoof localized surface plasmons generated by the structure can bind the energy on the surface of the structure and generate localized field enhancement. The space-filling design in this paper makes full use of the structure space. This highly localized structure can generate a higher Q-factor under the deep subwavelength structure, and the electromagnetic properties are not affected by the arbitrary bending of the metal structure, and have better stability. It provides a new idea for the preparation of nanometer-sized high-efficiency electromagnetic resonators.
-
-
图 1 梳型空间填充曲线结构示意图。
Figure 1. The schematic diagram of the structure of the comb-shaped space-filling curve.
图 2 不同周期数的单开口和双开口梳型结构的二维模拟仿真。
Figure 2. 2D simulation of single-opening and double-opening comb structures with different number of periods.
图 3 双开口梳型结构的高阶本征模计算。
Figure 3. Higher-order eigenmode calculations for double-open comb structures.
图 4 多种类型的空间填充曲线结构的人工局域表面等离激元共振特性。
Figure 4. 2D simulation of various types of space-filling curvilinear structures.
-
[1] Ritchie R H. Plasma losses by fast electrons in thin films[J]. Phys Rev A, 1957, 106(5): 874−881. doi: 10.1103/PhysRev.106.874
[2] Barnes W L, Dereux A, Ebbesen T W. Surface plasmon subwavelength optics[J]. Nature, 2003, 424(6950): 824−830. doi: 10.1038/nature01937
[3] Fang Z Y, Lu Y W, Fan L R, et al. Surface plasmon polariton enhancement in silver nanowire–nanoantenna structure[J]. Plasmonics, 2010, 5(1): 57−62. doi: 10.1007/s11468-009-9115-1
[4] Otto A. Excitation of nonradiative surface plasma waves in silver by the method of frustrated total reflection[J]. Z Physik, 1968, 216(4): 398−410. doi: 10.1007/BF01391532
[5] Andrew P, Barnes W L. Energy transfer across a metal film mediated by surface plasmon polaritons[J]. Science, 2004, 306(5698): 1002−1005. doi: 10.1126/science.1102992
[6] Faraday M X. The Bakerian Lecture. —Experimental relations of gold (and other metals) to light[J]. Philos Trans R Soc Lond, 1857, 147: 145−181.
[7] Huidobro P A, Shen X P, Cuerda J, et al. Magnetic localized surface plasmons[J]. Phys Rev X, 2014, 4(2): 021003. doi: 10.1103/PhysRevX.4.021003
[8] Pors A, Moreno E, Martin-Moreno L, et al. Localized spoof plasmons arise while texturing closed surfaces[J]. Phys Rev Lett, 2012, 108(22): 223905. doi: 10.1103/PhysRevLett.108.223905
[9] Viphavakit C, Boonruang S, Themistos C, et al. Surface plasmon resonance-enhanced light interaction in an integrated ormocomp nanowire[J]. Opt Quant Electron, 2016, 48(5): 291. doi: 10.1007/s11082-016-0499-9
[10] Li G H, Chen X S, Huang L J, et al. The localized near-field enhancement of metallic periodic bowtie structure: an oscillating dipoles picture[J]. Phys B Condens Matter, 2012, 407(12): 2223−2228. doi: 10.1016/j.physb.2012.03.003
[11] Polman A, Atwater H A. Photonic design principles for ultrahigh-efficiency photovoltaics[J]. Nat Mater, 2012, 11(3): 174−177. doi: 10.1038/nmat3263
[12] Zhang H C, Fan Y F, Guo J, et al. Second-harmonic generation of spoof surface plasmon polaritons using nonlinear plasmonic metamaterials[J]. ACS Photonics, 2016, 3(1): 139−146. doi: 10.1021/acsphotonics.5b00580
[13] Zhang H C, Zhang L P, He P H, et al. A plasmonic route for the integrated wireless communication of subdiffraction-limited signals[J]. Light Sci Appl, 2020, 9: 113. doi: 10.1038/s41377-020-00355-y
[14] Zhang H C, Liu S, Shen X P, et al. Broadband amplification of spoof surface plasmon polaritons at microwave frequencies[J]. Laser Photonics Rev, 2015, 9(1): 83−90. doi: 10.1002/lpor.201400131
[15] Krasavin A V, Zheludev N I. Active plasmonics: controlling signals in Au/Ga waveguide using nanoscale structural transformations[J]. Appl Phys Lett, 2004, 84(8): 1416−1418. doi: 10.1063/1.1650904
[16] Pacifici D, Lezec H J, Atwater H A. All-optical modulation by plasmonic excitation of CdSe quantum dots[J]. Nat Photonics, 2007, 1(7): 402−406. doi: 10.1038/nphoton.2007.95
[17] Wilson W D. Analyzing biomolecular interactions[J]. Science, 2002, 295(5562): 2103−2105. doi: 10.1126/science.295.5562.2103
[18] Novotny L, Hecht B. Principles of Nano-Optics[M]. Cambridge: Cambridge University Press, 2012.
[19] Wang S, Deng Z L, Wang Y J, et al. Arbitrary polarization conversion dichroism metasurfaces for all-in-one full Poincaré sphere polarizers[J]. Light Sci Appl, 2021, 10(1): 24. doi: 10.1038/s41377-021-00468-y
[20] Yu N F, Cubukcu E, Diehl L, et al. Bowtie plasmonic quantum cascade laser antenna[J]. Opt Express, 2007, 15(20): 13272−13281. doi: 10.1364/OE.15.013272
[21] Schnell M, García-Etxarri A, Huber A J, et al. Controlling the near-field oscillations of loaded plasmonic nanoantennas[J]. Nat Photonics, 2009, 3(5): 287−291. doi: 10.1038/nphoton.2009.46
[22] Atwater H A, Polman A. Plasmonics for improved photovoltaic devices[J]. Nat Mater, 2010, 9(3): 205−213. doi: 10.1038/nmat2629
[23] Heidel T D, Mapel J K, Singh M, et al. Surface plasmon polariton mediated energy transfer in organic photovoltaic devices[J]. Appl Phys Lett, 2007, 91(9): 093506. doi: 10.1063/1.2772173
[24] Fang C Z, Yang Q Y, Yuan Q C, et al. High-Q resonances governed by the quasi-bound states in the continuum in all-dielectric metasurfaces[J]. Opto-Electron Adv, 2021, 4(6): 200030. doi: 10.29026/oea.2021.200030
[25] Zhang Y B, Liu H, Cheng H, et al. Multidimensional manipulation of wave fields based on artificial microstructures[J]. Opto-Electron Adv, 2020, 3(11): 200002. doi: 10.29026/oea.2020.200002
[26] Wood R W. XLII. On a remarkable case of uneven distribution of light in a diffraction grating spectrum[J]. Lond Edinburgh Dublin Philos Mag J Sci, 1902, 4(21): 396−402. doi: 10.1080/14786440209462857
[27] Pendry J B, Martín-Moreno L, Garcia-Vidal F J. Mimicking surface plasmons with structured surfaces[J]. Science, 2004, 305(5685): 847−848. doi: 10.1126/science.1098999
[28] Hibbins A P, Evans B R, Sambles J R. Experimental verification of designer surface plasmons[J]. Science, 2005, 308(5722): 670−672. doi: 10.1126/science.1109043
[29] Williams C R, Andrews S R, Maier S A, et al. Highly confined guiding of terahertz surface plasmon polaritons on structured metal surfaces[J]. Nat Photonics, 2008, 2(3): 175−179. doi: 10.1038/nphoton.2007.301
[30] Luo Y, Chu C H, Vyas S, et al. Varifocal metalens for optical sectioning fluorescence microscopy[J]. Nano Lett, 2021, 21(12): 5133−5142. doi: 10.1021/acs.nanolett.1c01114
[31] Cai X D, Tang R, Zhou H Y, et al. Dynamically controlling terahertz wavefronts with cascaded metasurfaces[J]. Adv Photon, 2021, 3(3): 036003. doi: 10.1117/1.AP.3.3.036003
[32] Shen X P, Cui T J, Martin-Cano D, et al. Conformal surface plasmons propagating on ultrathin and flexible films[J]. Proc Natl Acad Sci USA, 2013, 110(1): 40−45. doi: 10.1073/pnas.1210417110
[33] Liao Z, Luo Y, Fernández-Domínguez A I, et al. High-order localized spoof surface plasmon resonances and experimental verifications[J]. Sci Rep, 2015, 5: 9590. doi: 10.1038/srep09590
[34] Liao Z, Pan B C, Shen X P, et al. Multiple Fano resonances in spoof localized surface plasmons[J]. Opt Express, 2014, 22(13): 15710−15717. doi: 10.1364/OE.22.015710
[35] Shi T, Deng Z L, Tu Q A, et al. Displacement-mediated bound states in the continuum in all-dielectric superlattice metasurfaces[J]. PhotoniX, 2021, 2: 7. doi: 10.1186/s43074-021-00029-x
[36] Deng Z L, Shi T, Krasnok A, et al. Observation of localized magnetic plasmon skyrmions[J]. Nat Commun, 2022, 13(1): 8. doi: 10.1038/s41467-021-27710-w
[37] Gao Z, Gao F, Xu H Y, et al. Localized spoof surface plasmons in textured open metal surfaces[J]. Opt Lett, 2016, 41(10): 2181−2184. doi: 10.1364/OL.41.002181
[38] Zhang X R, Cui T J. Deep-subwavelength and high-Q trapped mode induced by symmetry-broken in toroidal plasmonic resonator[J]. IEEE Trans Antenn Propag, 2021, 69(4): 2122−2129. doi: 10.1109/TAP.2020.3026480
-
下载:
点击扫一扫
图(6)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
