E-mail Alert
RSS
-
摘要
图像盲复原是仅从降质图像就恢复出模糊核和真实锐利图像的方法，由于其病态性，通常需要加入图像先验知识约束解的范围。针对传统的图像梯度l2和l1范数先验不能真实刻画自然图像梯度分布的特点，本文将图像梯度稀疏先验应用于单帧大气湍流退化图像盲复原中。先估计模糊核再进行非盲复原，利用分裂Bregman算法求解相应的非凸代价函数。仿真实验表明，与总变分先验(l1范数)相比，稀疏先验有利于模糊核的估计、产生锐利边缘和去除振铃等，降低了模糊核的估计误差从而提高了复原质量。最后对真实湍流退化图像进行了复原。
Abstract
Blind image deconvolution is one method of restoring both kernel and real sharp image only from degraded images, due to its illness, image priors are necessarily applied to constrain the solution. Given the fact that traditional image gradient l2 and l1 norm priors cannot describe the gradient distribution of natural images, in this paper, the image sparse prior is applied to the restoration of single-frame atmospheric turbulence degraded images. Kernel estimation is performed first, followed by non-blind restoration and the split Bregman algorithm is used to solve the non-convex cost function. Simulation results show that compared with total variation priori, sparse priori is better at kernel estimation, producing sharp edges and removal of ringing, etc., which reducing the kernel estimation error and improving restoration quality. Finally, the real turbulence-degraded images are restored.
-
Key words:
- adaptive optics /
- sparse prior /
- blind deconvolution /
- split Bregman
-
Overview
Overview: Atmospheric turbulence is a major factor limiting the imaging resolution of ground-based telescopes. Adaptive optics (AO) is commonly used to compensate for the wavefront distortion caused by turbulence to obtain higher resolution. However, due to the limitations of the system itself, such as the fitting error of the deformed mirror and the residual error caused by the time bandwidth, the closed-loop image still has residual errors, thus AO postprocessing technique is needed to further improve the image quality.
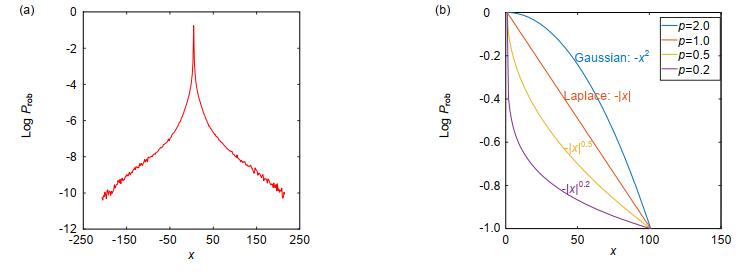
Blind deconvolution (BD) could recover a sharp image only from several degraded images. However, BD problems have the difficulties of ill-conditioned and infinite solutions, it is necessary to add prior knowledge to avoid undesired solutions. Traditional Wiener filtering based iterative blind deconvolution method assumes that the intensity of the image obeys the Gaussian distribution, while Chan et al. employ total variation prior, which assumes the gradient of the image obeys the Laplacian distribution. Given the fact that the gradient distribution of natural images is a sparse one with heavy tails, both of Gaussian and Laplacian model cannot approximate this sparse model greatly. Therefore, this paper draws on the image gradient sparse priori derived from blind motion deblurring, and applied it to the blind restoration of turbulence-degraded images.
In order to cope with the non-convex cost function caused by sparse prior, this paper uses split Bregman and look-up table method to solve effectively. Secondly, a two-step estimation strategy is adopted including kernel estimation and non-blind restoration. This paper employs the deconvolution method of Krishnan to reconstruct a sharp image with the kernel from the former step, and this strategy is essential to avoid the ringing effect reported by Fergus.
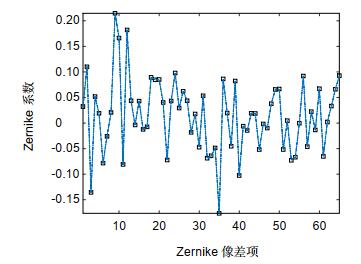
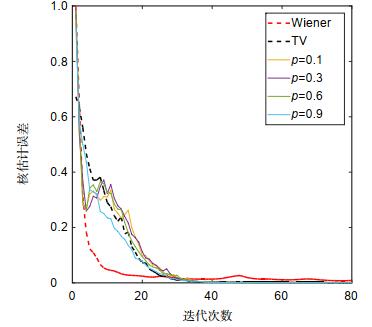
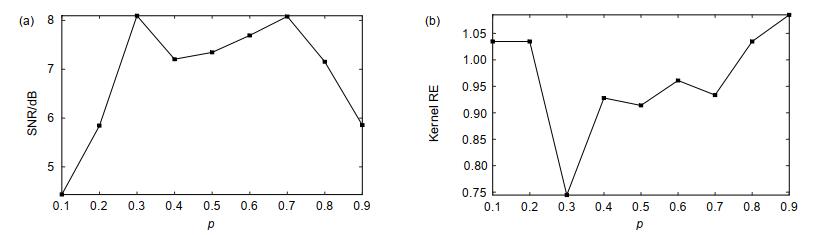
Firstly, the simulation experiment is carried out. To model the atmospheric turbulence degradation, the Zernike polynomials are used to generate the point spread function, and the OCNR5 satellite image is used as an object for observing. This paper adopts the relative error to evaluate the kernel estimation error and the signal to noise ratio (SNR) to evaluate image quality of degraded and restored ones. Both simulations and experiments on the real degraded images show that: 1) compared with the traditional Wiener filtering method and total variation prior, the sparse prior is beneficial to kernel estimation, produces sharp edges and removes ringing, thus improving the restoration quality. 2) After employing split Bregman optimization, restoration with sparse prior can converge rapidly and steadily, hence the proposed algorithm in this paper is robust and stable. 3) It is worth noting that the value of p should not be too large or too small, smaller p will amplify the noise.
-
-
图 1 自然图像统计模型。(a)真实自然图像的梯度分布；(b)参数模型
Figure 1. Natural images statistical model. (a) Real natural image gradient distribution; (b) Parametric model
图 2 仿真点扩散函数的Zernike系数分布
Figure 2. Simulated Zernike coefficient distribution of point spread function
图 3 仿真湍流降质图像的盲解卷积复原。
Figure 3. Blind deconvolution of simulated turbulence-degrade image.
图 5 不同p值下的复原图像SNRs和核估计误差RE
Figure 5. Restored image SNRs and kernel error RE under different p values
图 6 真实ISS退化图像复原。(a)退化图像; (b)总变分盲复原; (c)稀疏先验p=0.5复原; (d)稀疏先验p=0.1复原结果; (e)分别为(a), (b), (c)和(d)的局部细节
Figure 6. Real ISS restoration. (a) Degraded image; (b) Total variation restoration; (c) Sparse prior restoration with p=0.5; (d) Sparse prior restoration with p=0.1; (e) Local details of (a), (b), (c) and (d)
表 2 不同算法的核估计误差和信噪比
Table 2. Kernel estimation errors and SNRs of three algorithms
降质图像 维纳滤波盲复原 总变分盲复原 稀疏先验(p=0.9) 稀疏先验(p=0.6) 稀疏先验(p=0.3) 稀疏先验(p=0.1) 核估计相对误差 \ 1.1257 1.0805 1.0849 0.9610 0.7445 0.8528 SNR/dB 5.204 2.093 5.548 5.855 7.691 8.096 5.843 运行时间/s \ 10.34 17.3 24.34 27.78 25.12 28.25 
下载: 导出CSV
-
参考文献
[1] 姜文汉.自适应光学技术[J].自然杂志, 2006, 28(1): 7-13. doi: 10.3969/j.issn.0253-9608.2006.01.002
Jiang W H. Adaptive optical technology[J]. Chinese Journal of Nature, 2006, 28(1): 7-13. doi: 10.3969/j.issn.0253-9608.2006.01.002
[2] 鲍华, 饶长辉, 田雨, 等.自适应光学图像事后重建技术研究进展[J].光电工程, 2018, 45(3): 58-67. doi: 10.12086/oee.2018.170730
Bao H, Rao C H, Tian Y, et al. Research progress on adaptive optical image post reconstruction[J]. Opto-Electronic Engineering, 2018, 45(3): 58-67. doi: 10.12086/oee.2018.170730
[3] Levin A, Weiss Y, Durand F, et al. Understanding and evaluating blind deconvolution algorithms[C]//Proceedings of 2009 IEEE conference on Computer Vision and Pattern Recognition, Miami, 2009: 1964-1971.
[4] Perrone D, Favaro P. Total variation blind deconvolution: the devil is in the details[C]//Proceedings of 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, 2014: 2909-2916.
[5] Ayers G R, Dainty J C. Iterative blind deconvolution method and its applications[J]. Optics Letters, 1988, 13(7): 547-549. doi: 10.1364/OL.13.000547
[6] Lane R G. Blind deconvolution of speckle images[J]. Journal of the Optical Society of America A, 1992, 9(9): 1508-1514. doi: 10.1364/JOSAA.9.001508
[7] Jefferies S M, Christou J C. Restoration of astronomical images by iterative blind deconvolution[J]. Astrophysical Journal, 1993, 415(2): 862-874. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=CC0210508829
[8] You Y L, Kaveh M. A regularization approach to joint blur identification and image restoration[J]. IEEE Transactions on Image Processing, 1996, 5(3): 416-428. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=c9eb1ee764cb21dd174d629b0d735283
[9] Chan T F, Wong C K. Total variation blind deconvolution[J]. IEEE Transactions on Image Processing, 1998, 7(3): 370-375. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=ee858cf32523ce9f1f52d11cad9788db
[10] Fergus R, Singh B, Hertzmann A, et al. Removing camera shake from a single photograph[J]. ACM Transactions on Graphics, 2006, 25(3): 787-794. doi: 10.1145/1141911.1141956
[11] Krishnan D, Tay T, Fergus R. Blind deconvolution using a normalized sparsity measure[C]//Proceedings of the 24th IEEE Conference on Computer Vision and Pattern Recognition, Providence, 2011: 233-240.
[12] Kotera J, Šroubek F, Milanfar P. Blind deconvolution using alternating maximum a posteriori estimation with heavy-tailed priors[C]//Proceedings of the 15th International Conference on Computer Analysis of Images and Patterns, York, 2013: 59-66.
[13] Goldstein T, Osher S. The split bregman method for L1-regularized problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(2): 323-343. doi: 10.1137/080725891
[14] Krishnan D, Fergus R. Fast image deconvolution using hyper-Laplacian priors[C]//Proceedings of the 22nd International Conference on Neural Information Processing Systems, Vancouver, 2009: 1033-1041.
[15] Chan T F, Wong C K. Convergence of the alternating minimization algorithm for blind deconvolution[J]. Linear Algebra and its Applications, 2000, 316(1-3): 259-285. doi: 10.1016/S0024-3795(00)00141-5
[16] Levin A, Fergus R, Durand F, et al. Image and depth from a conventional camera with a coded aperture[J]. ACM Transactions on Graphics, 2007, 26(3): 70. doi: 10.1145/1276377.1276464
[17] 王齐涛, 佟首峰, 徐友会.采用Zernike多项式对大气湍流相位屏的仿真和验证[J].红外与激光工程, 2013, 42(7): 1907-1911. doi: 10.3969/j.issn.1007-2276.2013.07.046
Wang Q T, Tong S F, Xu Y H. On simulation and verification of the atmospheric turbulent phase screen with Zernike polynomials[J]. Infrared and Laser Engineering, 2013, 42(7): 1907-1911. doi: 10.3969/j.issn.1007-2276.2013.07.046
-
访问统计
点击扫一扫
图(6)
表(2)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
