E-mail Alert
RSS
Single-frame far-field wavefront retrieval method based on Walsh function modulation
-
摘要
单帧远场图像重构波前像差的方法在结构简便性方面有独特的优势。然而，传统的基于单帧远场图像的波前重构算法存在多解问题，算法收敛过程容易陷入停滞。本文在分析单帧相位反演方法的多解问题成因的基础上，提出了一种基于Walsh函数的二维离散相位调制的波前重构方法。此种方法可以有效地打破近场波前的对称性，解决多解问题。仿真结果表明，该方法只需一个远场图像就可以精确地重建波前像差。
Abstract
The reconstruction of wavefront from single far-field image data has unique advantages in simplicity of structure. However, the traditional wavefront reconstruction algorithm has multiple solutions based on single far-field image, its iterative process easily falls into stagnation. In this paper, based on the analysis of the multi-solution problem of single-frame phase retrieval method, a wavefront reconstruction method based on Walsh function two-dimensional discrete phase modulation is proposed. This method can effectively break the symmetry of near-field wavefront and overcome problem of multiple solutions. The simulation results show that the method can accurately reconstruct wavefront aberration with only one far-field image.
-
Key words:
- phase retrieval /
- aberration /
- far-field /
-
-
Overview
Overview: Phase retrieval (PR) is an iterative process of wavefront recovering from known intensity distribution. Owing to high detection accuracy and lower environment requirement, PR has become an attractive candidate to the wavefront sensor (WFS) in adaptive optics. With the development of computer speed, PR will have greater potentiality in active optic systems.
Gerchberg and Saxton proposed firstly the GS algorithm to recover the wavefront aberration. This algorithm can achieve typical convergence, but its iterative process easily falls into stagnation. For instance, the true pupil field f(x, y) and its twin f*(-x, -y) have the same Fourier modulus, so the algorithm tries to recover both together and goes nowhere. For overcoming the two-fold ambiguity of GS algorithm, phase diversity (PD) algorithm was proposed by Gonsalves in 1979. However, this method introduces a defocused plane to increase the constrained intensity information to reconstruct the wavefront, which will sacrifice the simplicity. Löfdahl proposed PD sensor with a beam splitter to make the focus and defocused images be captured by one CCD. For the same purpose a PD sensor with a distorted diffraction grating was presented by Blanchard in 2000. Nevertheless, more complex structure, interaction of high frequency information and dynamic range of CCD limit the practical application of these methods in the PD.
In 2008, Min Li and Xinyang Li proposed a method based on the linear phase retrieval (LPR) to reconstruct small aberrations from a single far field image. In 2010, the linearized focal plane technique (LIFT) was presented by Serge Meimon, which is only effective for lower order aberration. Bing Dong et al demonstrated a hybrid phase retrieval algorithm using a combination of LPR and GS in 2015. The estimation result of LPR is used as a prior knowledge to speed convergence of GS. In this way, the higher order aberrations are basically recovered, but the problem of multiple solutions remains unsolved.
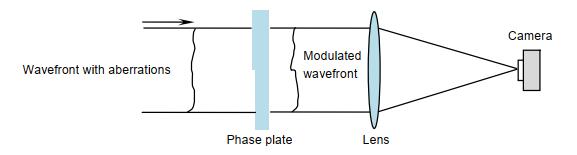
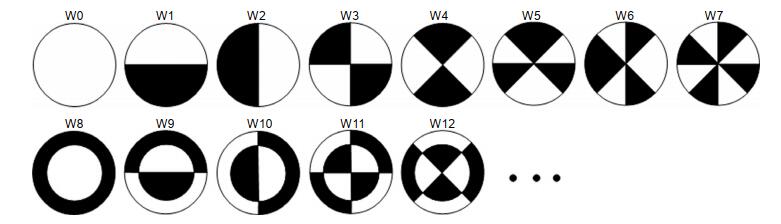
In order to solve the problems mentioned above in traditional single-frame phase retrieval algorithm, a feasible method is proposed to break the rotational symmetry of near-field wavefront phase. If continuous aberration is used for wavefront modulation, it is equivalent to adding a wavefront on the measured wavefront. This cannot solve the problem of multiple solutions.
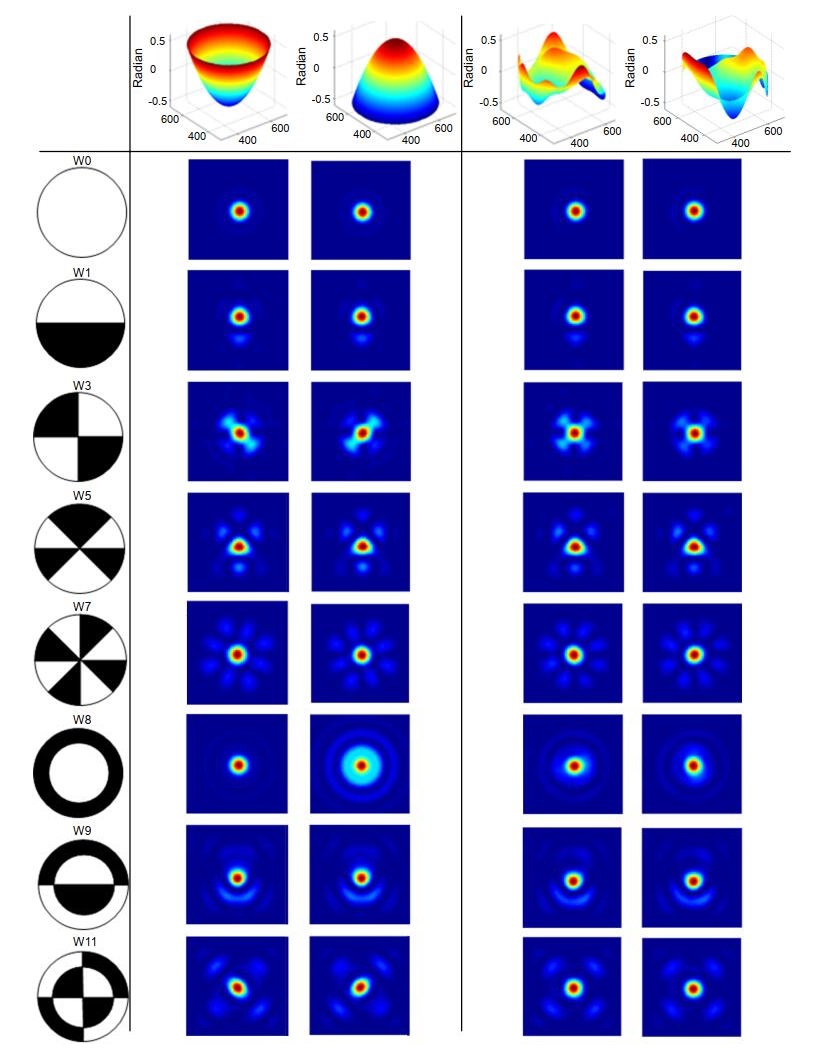
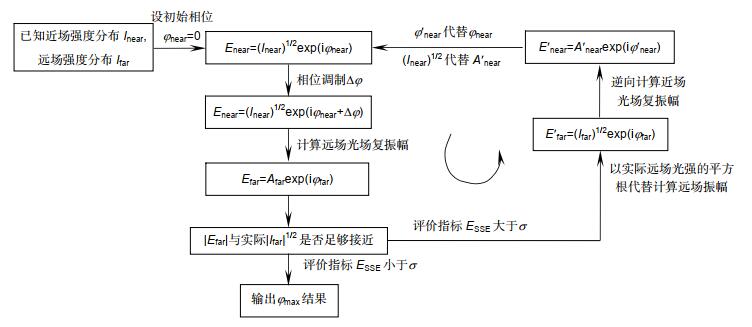
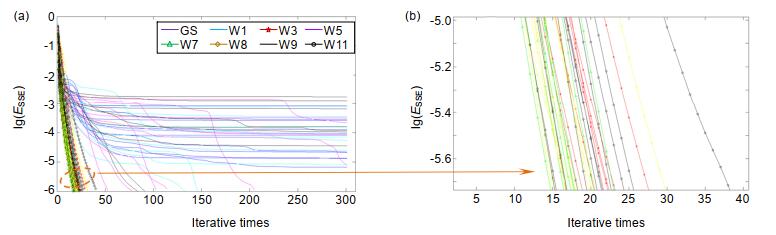
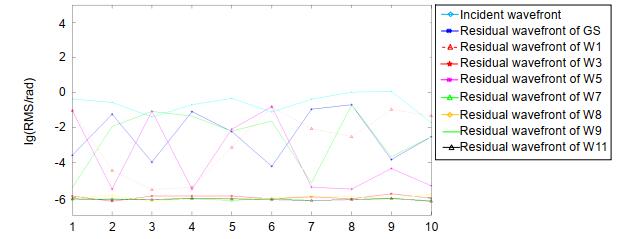
A wavefront reconstruction method based on Walsh function two-dimensional discrete phase modulation is proposed in this paper. This method can effectively break the symmetry of near-field wavefront and overcome problem of PR multiple solutions. The basic principle and limitation of this method are introduced. The wavefront retrieval accuracy of the proposed algorithm is compared to the traditional GS algorithm through simulations and experiments. The results show that the wavefront retrieval algorithm based on phase modulation of Walsh function can accurately reconstruct the wavefront aberration under the condition of single far-field image.
-
-
图 4 基于Walsh函数调制的相位反演算法流程图
Figure 4. Flow chart of PR algorithm based on Walsh function modulation
图 5 待测波前。(a)波形；(b) Zernike系数
Figure 5. Test wavefront. (a) Waveform; (b) Zernike coefficient
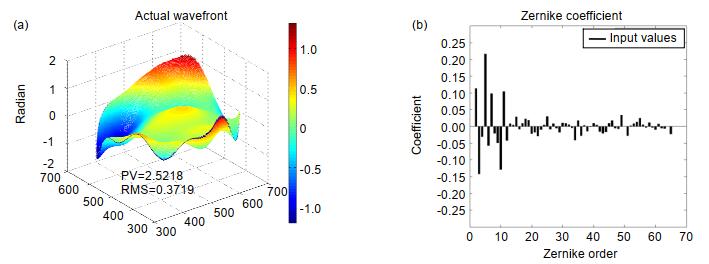
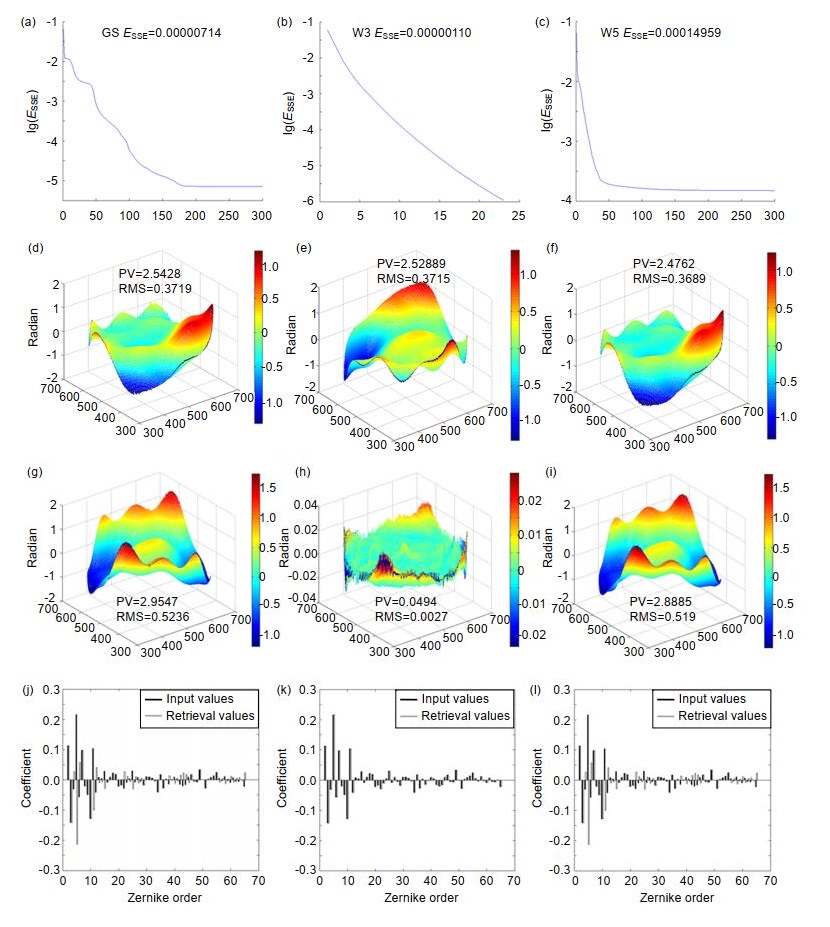
图 6 波前重建结果。(a) GS评估指标ESSE的收敛曲线；(b) W3调制评估指标ESSE的收敛曲线；(c) W5调制评估指标ESSE的收敛曲线；(d) GS算法的重构波前；(e) W3调制的重构波前；(f) W5调制的重构波前；(g) GS的残余波前；(h) W3调制的残余波前；(i) W5调制的残余波前；(j) GS的系数重构；(k) W3调制的系数重构；(l) W5调制的系数重构
Figure 6. Wavefront reconstructed results. (a) The convergence line of evaluation index ESSE of GS; (b) The convergence line of evaluation index ESSE of W3 modulation; (c) The convergence line of evaluation index ESSE of W5 modulation; (d) Reconstructed wavefront of GS; (e) Reconstructed wavefront of W3 modulation; (f) Reconstructed wavefront of W5 modulation; (g) Wavefront reconstruction residual error of GS; (h) Wavefront reconstruction residual error of W3 modulation. (i) Wavefront reconstruction residual error of W5 modulation; (j) Coefficient reconstruction of GS; (k) Coefficient reconstruction of W3 modulation; (l) Coefficient reconstruction of W5 modulation
图 7 传统GS算法和Walsh函数调制算法的迭代曲线
Figure 7. Convergence lines of traditional GS algorithm and Walsh function modulation algorithms
图 8 不同相位反演方法的残余波前RMS值比较图
Figure 8. RMS value comparison diagram of residual wavefront of different PR methods
-
参考文献
[1] Védrenne N, Mugnier L M, Michau V, et al. Laser beam complex amplitude measurement by phase diversity[J]. Optics Express, 2014, 22(4): 4575–4589. doi: 10.1364/OE.22.004575
[2] Gonsalves R A. Phase retrieval and diversity in adaptive optics[J]. Optical Engineering, 1982, 21(5): 215829. https://www.spiedigitallibrary.org/journals/Optical-Engineering/volume-21/issue-5/215829/Phase-Retrieval-And-Diversity-In-Adaptive-Optics/10.1117/12.7972989.full
[3] 姜文汉.自适应光学发展综述[J].光电工程, 2018, 45(3): 170489. doi: 10.12086/oee.2018.170489
Jiang W H. Overview of adaptive optics development[J]. Opto-Electronic Engineering, 2018, 45(3): 170489. doi: 10.12086/oee.2018.170489
[4] Wu J, Chen J B. A phase retrieval algorithm for X-ray phase contrast imaging[J]. Optik, 2013, 124(9): 864–866. doi: 10.1016/j.ijleo.2012.02.030
[5] Wu X Z, Yan A M. Phase retrieval from one single phase contrast X-ray image[J]. Optics Express, 2009, 17(13): 11187–11196. doi: 10.1364/OE.17.011187
[6] Fienup J R, Marron J C, Schulz T J, et al. Hubble Space Telescope characterized by using phase-retrieval algorithms[J]. Applied Optics, 1993, 32(10): 1747–1767. doi: 10.1364/AO.32.001747
[7] Hartung M, Blanc A, Fusco T, et al. Calibration of NAOS and CONICA static aberrations experimental results[J]. Astronomy & Astrophysics, 2003, 399(1): 386–394. https://ui.adsabs.harvard.edu/abs/2003A%26A...399..385H/abstract
[8] 鲍华, 饶长辉, 田雨, 等.自适应光学图像事后重建技术研究进展[J].光电工程, 2018, 45(3): 170730. doi: 10.12086/oee.2018.170730
Bao H, Rao C H, Tian Y, et al. Research progress on adaptive optical image post reconstruction[J]. Opto-Electronic Engineering, 2018, 45(3): 170730. doi: 10.12086/oee.2018.170730
[9] Gerchberg R W, Saxton W O. A practical algorithm for the determination of phase from image and diffraction plane pictures[J]. Optik, 1972, 35(2): 237–246. https://www.researchgate.net/publication/221725051_A_practical_algorithm_for_the_determination_of_phase_from_image_and_diffraction_plane_pictures
[10] Fienup J R, Wackerman C C. Phase-retrieval stagnation problems and solutions[J]. Journal of the Optical Society of America A, 1986, 3(11): 1897–1907. doi: 10.1364/JOSAA.3.001897
[11] Greenbaum A Z, Sivaramakrishnan A. In-focus wavefront sensing using non-redundant mask-induced pupil diversity[J]. Optics Express, 2016, 24(14): 15506–15521. doi: 10.1364/OE.24.015506
[12] Li M, Li X Y, Jiang W H. Small-phase retrieval with a single far-field image[J]. Optics Express, 2008, 16(11): 8190–8197. doi: 10.1364/OE.16.008190
[13] Li M, Li X Y. Linear phase retrieval with a single far-field image based on Zernike polynomials[J]. Optics Express, 2009, 17(17): 15257–15263. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=Open J-Gate000001402353
[14] Meimon S, Fusco T, Mugnier L M. LIFT: a focal-plane wavefront sensor for real-time low-order sensing on faint sources[J]. Optics Letters, 2010, 35(18): 3036–3038. doi: 10.1364/OL.35.003036
[15] Wang F L. Wavefront sensing through measurements of binary aberration modes[J]. Applied Optics, 2009, 48(15): 2865–2870. doi: 10.1364/AO.48.002865
[16] Wang S, Yang P, Ao M W, et al. Wavefront sensing by means of binary intensity modulation[J]. Applied Optics, 2014, 53(35): 8342–8349. doi: 10.1364/AO.53.008342
-
访问统计
下载:
点击扫一扫
图(9)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
