E-mail Alert
RSS
-
摘要:
悬链线型亚波长结构可以实现连续的相位调控。但是，普通悬链线孔径两端较窄，不易于加工。另外，以往直接在仿真软件CST中建立复杂模型较为困难，仿真过程较为繁琐。本文提出了用等宽悬链线狭缝替代普通悬链线狭缝，并设计了用于产生贝塞尔光束的等宽悬链线超表面，为二维光电器件的设计提供了新思路。在建模仿真过程中使用Matlab调用CST进行联合仿真，直接在Matlab中完成所有建模、仿真、修改参数等操作。该方法可以用于设计复杂结构，同时结合Matlab数值优化能力得到更理想的仿真效果。
Abstract:Catenary nanostructures enable continuous phase control. However, the ordinary catenary nanostructure has narrow width at both ends and is not easy to be fabricated. On the other side, it was difficult to build complex model directly in simulation software CST, and the simulation process was complicated in the past. The equal-width catenary slit is proposed to replace the normal catenary slit. And the equal-width catenary-type metasurface has been designed to generate Bessel beam, which provides a new idea for the design of two-dimensional optical devices. In the process of modeling and simulation, CST is combined with Matlab for co-simulation, and all operations, such as modeling, simulations, and parameter modification, are completed directly in Matlab. This method can be used to design complex structures, and more ideal simulation results can be obtained combined with the numerical optimization ability of Matlab.
-
Key words:
- metasurfaces /
- catenary /
- Bessel beam /
- CST /
- Matlab
-
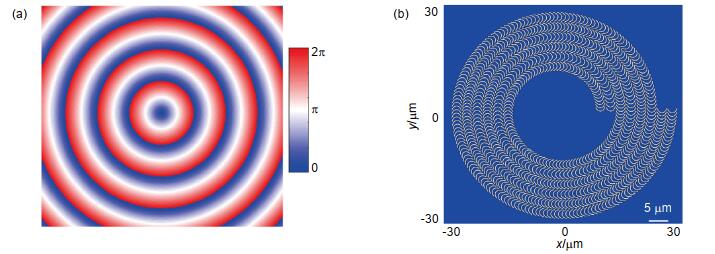
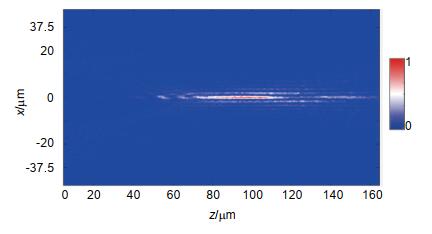
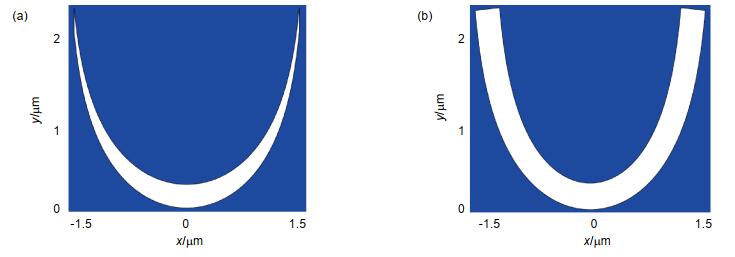
Overview: The metasurface is an ultra-thin two-dimensional material arranged by metal or dielectric subwavelength structures. Phase-modulated metasurface is an important branch of metasurfaces, which mainly includes propagation, geometric, and circuit-type phase metasurfaces. The phase modulation of incident circular polarization can be realized in geometric phase metasurfaces by using the spatially varying subwavelength structure. Usually, the geometric phase metasurface is realized by discrete structures whose rotation angle has a correspondence with the geometric phase. However, discrete elements can only generate discrete phase distributions. Catenary is a kind of mechanical curves. The geometric phase metasurfaces composed of catenary structures can realize continuous geometric phase. The catenary metasurface is composed of catenary slits etched on the metal film. The slit is translated down by a catenary and the two ends are connected. Similar to discrete metasurfaces, catenary slits can be considered as a patchwork of discrete elements. The tangent angle of the catenary corresponds to the rotation angle of the coordinate system of the discrete element. As described above, catenary slit is composed of vertical-translated catenary, so both ends of the slit will be very narrow, which is not conducive to experimental processing. Therefore, it is necessary to design equal-width catenary metasurfaces. On the other hand, in the design and simulation of the metasurfaces, CST is usually used for modeling and simulations. When designing V-shaped antennas, rectangular apertures, and other subwavelength structures such as normal catenary slits, the modeling process can be performed directly in CST. However, it is more complex for equal-width catenary slits and other irregularly shaped structures. On the other hand, when it comes to the need to optimize the arrangement of subwavelength element array, it is necessary to repeatedly model in CST, but to analyze data and optimize the structure in Matlab, which will affect the work efficiency. In previous studies, researchers have proposed co-simulation with Matlab and CST. Because of the software version, the purpose of the work, and the CST's numerous underlying commands, however, it is difficult to reproduce. In this paper, when designing the catenary metasurfaces, Matlab R2016b is used to call CST Microwave Studio version 2016 for modeling and simulations. A two-dimensional Bessel beam generator composed of an array of equal-width catenary slits is obtained. This article also tells the details of the co-simulation, so that researchers can better apply it to their own work.
-
-
图 1 悬链线狭缝结构示意图。(a)普通悬链线狭缝；(b)等宽悬链线狭缝
Figure 1. Diagrams of catenary slits. (a) Ordinary catenary slit; (b) Equal-width catenary slit
图 2 等宽悬链线阵列结构。(a)零阶贝塞尔光束相位分布图；(b)等宽悬链线零阶贝塞尔光束产生器件
Figure 2. Equal-width catenary array structure. (a) Phase distribution of zero-order Bessel beam generator; (b) Zero-order Bessel beam generator constructed by equal-width catenary arrays
图 5 CST仿真得到的x-z平面Bessel光束光强分布
Figure 5. Intensity distribution of Bessel beam on x-z plane obtained by CST
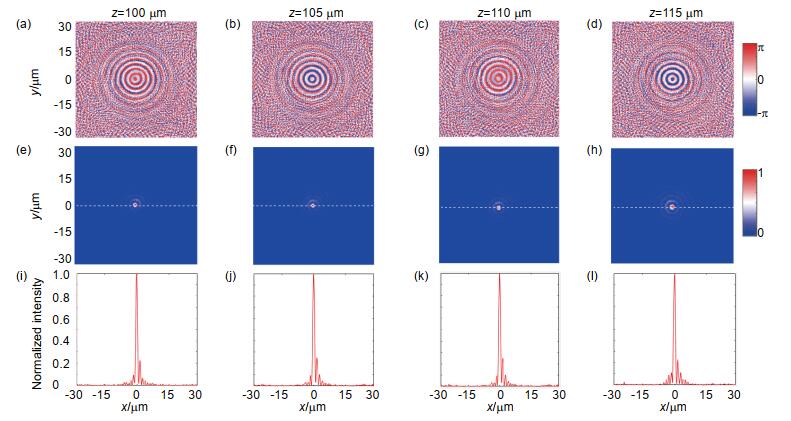
图 6 x-y平面贝塞尔光束光强和相位分布。(a)~(d)距离结构一定距离处，x-y平面贝塞尔光束相位分布；(e)~(h)与相位对应的光强分布图；(i) ~ (l)图(e) ~ (h)虚线所示的光强截线图
Figure 6. Intensity and phase distributions of Bessel beam on x-y plane. (a)~(d) Represent the phase distributions on x-y plane at certain distances from the structure; (e)~(h) Denote the intensity distributions corresponding to the phase distributions (a)~(d), respectively; (i)~(l) are the cross views of the intensity shown by the dashed lines in figures (e)~(h), respectively
表 1 Matlab和CST联合仿真的基本语句
Table 1. Basic codes of Matlab and CST co-simulation
Function Code Calling CST cst=actxserver(‘CSTStuio.application’) Creating new MWS file mws=cst.invoke(‘NewMWS’); Saving MWS file mws.invoke(‘saveas’, ‘Bessl.cst’); Saving MWS file mws.invoke(‘AddToHistory’, VBA); 
下载: 导出CSV
-
[1] Durnin J. Exact solutions for nondiffracting beams. Ⅰ. The scalar theory[J]. Journal of the Optical Society of America A, 1987, 4(4): 651-654. doi: 10.1364/JOSAA.4.000651
[2] Moreno I, Davis J A, Sánchez-López M M, et al. Nondiffracting Bessel beams with polarization state that varies with propagation distance[J]. Optics Letters, 2015, 40(23): 5451-5454. doi: 10.1364/OL.40.005451
[3] Bliokh K Y, Rodríguez-Fortuño F J, Nori F, et al. Spin-orbit interactions of light[J]. Nature Photonics, 2015, 9(12): 796-808. doi: 10.1038/nphoton.2015.201
[4] Yu N F, Genevet P, Kats M A, et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction[J].Science, 2011, 334(6054): 333-337. doi: 10.1126/science.1210713
[5] Pu M B, Zhao Z Y, Wang Y Q, et al. Spatially and spectrally engineered spin-orbit interaction for achromatic virtual shaping[J]. Scientific Reports, 2015, 5: 9822. doi: 10.1038/srep09822
[6] Li X, Chen L W, Li Y, et al. Multicolor 3D meta-holography by broadband plasmonic modulation[J]. Science Advances, 2016, 2(11): e1601102. doi: 10.1126/sciadv.1601102
[7] Schurig D, Mock J J, Justice B J, et al. Metamaterial electromagnetic cloak at microwave frequencies[J]. Science, 2006, 314(5801): 977-980. doi: 10.1126/science.1133628
[8] Zhang J, Mei Z L, Zhang W R, et al. An ultrathin directional carpet cloak based on generalized Snell's law[J]. Applied Physics Letters, 2013, 103(15): 151115. doi: 10.1063/1.4824898
[9] Leonhardt U. Optical conformal mapping[J]. Science, 2006, 312(5781): 1777-1780. doi: 10.1126/science.1126493
[10] Ma X L, Pu M B, Li X, et al. All-metallic wide-angle metasurfaces for multifunctional polarization manipulation[J]. Opto-Electronic Advances, 2019, 2(3): 180023. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gdjz-e201903002
[11] Nemati A, Wang Q, Hong M H, et al. Tunable and reconfigurable metasurfaces and metadevices[J]. Opto-Electronic Advances, 2018, 1(5): 180009. http://d.old.wanfangdata.com.cn/Periodical/gdjz-e201805002
[12] Rahmani M, Leo G, Brener I, et al. Nonlinear frequency conversion in optical nanoantennas and metasurfaces: materials evolution and fabrication[J]. Opto-Electronic Advances, 2018, 1(10): 180021. http://www.oejournal.org/J/OEA/Article/Details/A181207000001
[13] Luo X G. Principles of electromagnetic waves in metasurfaces[J]. Science China Physics, Mechanics & Astronomy, 2015, 58(9): 594201. http://engine.scichina.com/publisher/scp/journal/SCPMA/58/9/10.1007/s11433-015-5688-1?slug=abstract
[14] Li X, Ma X L, Luo X G. Principles and applications of metasurfaces with phase modulation[J]. Opto-Electronic Engineering, 2017, 44(3): 255-275. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gdgc201703003
[15] Jin J J, Luo J, Zhang X H, et al. Generation and detection of orbital angular momentum via metasurface[J]. Scientific Reports, 2016, 6: 24286. doi: 10.1038/srep24286
[16] Gao H, Pu M B, Li X, et al. Super-resolution imaging with a Bessel lens realized by a geometric metasurface[J]. Optics Express, 2017, 25(12): 13933-13943. doi: 10.1364/OE.25.013933
[17] Luo X G, Pu M B, Li X, et al. Broadband spin Hall effect of light in single nanoapertures[J]. Light: Science & Applications, 2017, 6(6): e16276. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gkxyyy-e201702029
[18] Li X, Pu M B, Zhao Z Y, et al. Catenary nanostructures as compact Bessel beam generators[J]. Scientific Reports, 2016, 6: 20524. doi: 10.1038/srep20524
[19] Pu M B, Li X, Ma X L, et al. Catenary optics for achromatic generation of perfect optical angular momentum[J]. Science Advances, 2015, 1(9): e1500396. doi: 10.1126/sciadv.1500396
[20] Hasman E, Kleiner V, Biener G, et al. Polarization dependent focusing lens by use of quantized Pancharatnam-Berry phase diffractive optics[J]. Applied Physics Letters, 2003, 82(3): 328-330. doi: 10.1063/1.1539300
-
点击扫一扫
图(6)
表(1)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
