E-mail Alert
RSS
-
摘要
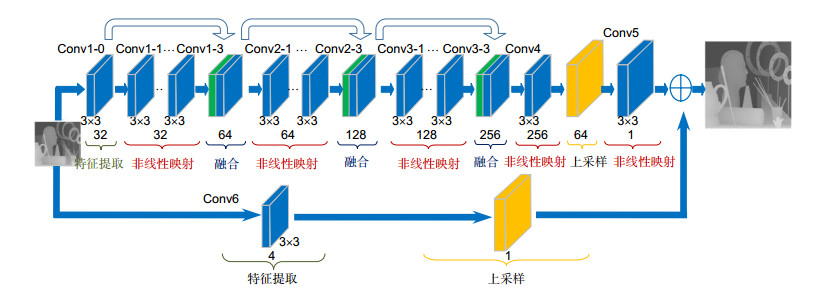
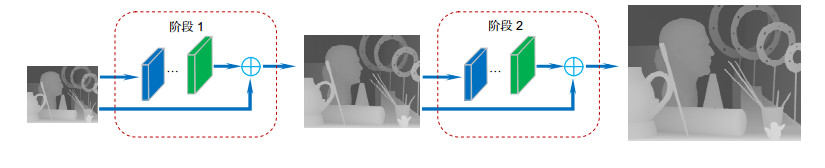
由于成像设备的限制，深度图往往分辨率较低。对低分辨率深度图进行上采样时，通常会造成深度图的边缘模糊。当上采样因子较大时，这种问题尤为明显。本文提出金字塔密集残差网络，实现深度图超分辨率重建。整个网络以残差网络为主框架，采用级联的金字塔结构对深度图分阶段上采样。在每一阶段，采用简化的密集连接块获取图像的高频残差信息，尤其是底层的边缘信息，同时残差结构中的跳跃连接分支获取图像的低频信息。网络直接以原始低分辨率深度图作为输入，以亚像素卷积层进行上采样操作，减少了运算复杂度。实验结果表明，该方法有效地解决了图像深度边缘的模糊问题，在定性和定量评价上优于现有方法。
Abstract
Due to the limitation of equipment, the resolution of depth map is low. Depth edges often become blurred when the low-resolution depth image is upsampled. In this paper, we present the pyramid dense residual network (PDRN) to efficiently reconstruct the high-resolution images. The network takes residual network as the main frame and adopts the cascaded pyramid structure for phased upsampling. At each pyramid level, the modified dense block is used to acquire high frequency residual, especially the edge features and the skip connection branch in the residual structure is used to deal with the low frequency information. The network directly uses the low-resolution depth image as the initial input of the network and the subpixel convolution layers is used for upsampling. It reduces the computational complexity. The experiments indicate that the proposed method effectively solves the problem of blurred edge and obtains great results both in qualitative and quantitative.
-
Key words:
- depth map /
- super-resolution /
- pyramid /
- dense residual
-
Overview
Overview: With the development of science and technology, depth information is gradually applied to various fields of society, such as face recognition, virtual reality and so on. However, due to the limitation of hardware conditions such as sensors, the resolution of the depth images is too low to meet the requirements of the reality. Depth map super- resolution has been an important research area in the field of computer vision. Early methods adopt interpolation, filtering. Although these methods are simple and fast in running, the clues used by these methods are limited and the results are not ideal. The details of the depth map is lost, especially when the upsampling factor is large. To address the above issue, intensity images are used to guide the depth map super-resolution. But when the local structures in the guidance and depth images are not consistent, these techniques may cause the over-texture transferring problem. At present, convolutional neural networks are widely used in computer vision because of its powerful feature representation ability. Several models based on convolutional neural networks have achieved great success in single image super-resolution. To solve the problems of edge blurring and over-texture transferring in depth super-resolution, we propose a new framework to achieve single depth image super-resolution based on the pyramid dense residual network (PDRN). The PDRN directly uses the low-resolution depth image as the input of the network and doesn't require the pre-processing. This can reduce the computational complexity and avoid the additional error. The network takes the residual network as the backbone model and adopts the cascaded pyramid structure for phased upsampling. The result of each pyramid stage is used as the input of the next stage. At each pyramid stage, the modified dense block is used to acquire high frequency residual, and subpixel convolution layer is used for upsampling. The dense block enhances transmission of feature and reduces information loss. Therefore, the network can reconstruct high resolution depth maps using different levels of features. The residual structure is used to shorten the time of convergence and improve the accuracy. In addition, the network adopts the Charbonnier loss function to train the network. By constraining the results of each stage, the training network can get more stable results. Experiments show that the proposed network can avoid edge blurring, detail loss and over-texture transferring in depth map super-resolution. Extensive evaluations on several datasets indicate that the proposed method obtains better performance comparing to other state-of-the-art methods.
-
-
图 1 整体网络结构。该图是上采样因子为4时的结构图，包含2个阶段。每个阶段上采样因子为2，一个阶段的输出作为下一阶段的输入
Figure 1. The network structure. It is for upscale factor 4 that contains two stages. The upscale factor for each stage is 2 and the output of one stage is used as the input of the next stage
图 2 金字塔密集残差网络(PDRN)单阶段网络结构，上采样因子为2。该结构包含四种运算：特征提取、非线性映射、融合、上采样
Figure 2. The single stage of the pyramid dense residual network (PDRN) for upscale factor 2. It contains four operations: feature extraction, non-linear, fusion and upsampling
图 3 重建结果图及频谱分析图。(a)最终结果图及对应的谱分析图；(b)子带残差结果图及其频谱图；(c)跳跃连接分支结果图及其频谱图
Figure 3. Reconstruction results and spectrum analysis. (a) Final result and corresponding spectrum analysis; (b) Residual result and its spectrum analysis; (c) Skip connection result and its spectrum analysis
图 4 (a) 常见的密集连接块；(b)本文采用的密集连接块，通过跳跃连接，特征图的数量由32增加到256
Figure 4. (a) The original dense block; (b) Our dense block that the number of feature maps is changed from 32 to 256 through three skip connections
图 5 上采样为4的重建结果。(a)真实深度图；(b)最近邻插值；(c)双三次插值；(d) PDN；(e)本文方法
Figure 5. Reconstruction results for scale factor 4. (a) Ground truth; (b) Nearest; (c) Bicubic; (d) PDN; (e) PDRN
表 1 有无残差结构在数据集Laser Scan的定量评价(RMSE/SSIM)
Table 1. Quantitative comparison (in RMSE and SSIM) on dataset Laser Scan
Scan1 Scan2 Scan3 2× 4× 8× 2× 4× 8× 2× 4× 8× Nearest 5.401/0.9820 8.567/0.9573 13.02/0.9176 4.251/0.9841 6.701/0.9630 9.992/0.9301 4.540/0.9842 8.112/0.9560 11.15/0.9218 Bicubic 4.215/0.9864 6.496/0.9689 10.09/0.9377 3.477/0.9873 5.234/0.9734 7.825/0.9505 4.063/0.9865 6.415/0.9658 8.930/0.9385 PDN 2.480/0.9917 3.754/0.9873 5.542/0.9791 2.106/0.9921 3.139/0.9880 4.455/0.9809 1.861/0.9951 2.889/0.9920 4.196/0.9866 PDRN 2.170/0.9923 3.612/0.9878 5.391/0.9797 1.800/0.9927 3.041/0.9884 4.355/0.9815 1.303/0.9962 2.695/0.9926 4.006/0.9876 
下载: 导出CSV
表 2 数据集A上重建结果的定量评价(RMSE)
Table 2. Quantitative comparison (in RMSE) on dataset A
Art Books Moebius 2× 4× 8× 16× 2× 4× 8× 16× 2× 4× 8× 16× Bicubic 2.5837 3.8565 5.5282 8.3759 1.0321 1.5794 2.2693 3.3652 0.9304 1.4006 2.0581 2.9702 MRF[24] 3.0192 3.6693 5.3349 8.3815 1.1976 1.5359 2.2026 3.4137 1.1665 1.4104 1.9905 2.9874 Guided[4] 2.8449 3.6686 4.8252 7.5978 1.1607 1.5646 2.0843 3.1856 1.0748 1.4029 1.8258 2.7592 Edge[25] 2.7502 3.4110 4.0320 6.0719 1.0611 1.5216 1.9754 2.7581 1.0501 1.3372 1.7863 2.3511 TGV[3] 2.9216 3.6474 4.6034 6.8204 1.2818 1.5841 1.9692 2.9503 1.1136 1.4302 1.8397 2.5216 AP[27] 1.7909 2.8513 3.6943 5.9113 1.3280 1.5297 1.8394 2.9187 0.8704 1.0311 1.5505 2.5728 SRCNN[13] 1.1338 2.0175 3.8293 7.2717 0.5231 0.9356 1.7268 3.1006 0.5374 0.9132 1.5790 2.6896 VDSR[15] 1.3242 2.0710 3.2433 6.6622 0.4883 0.8296 1.2878 2.1433 0.5441 0.8341 1.2952 2.1590 MS-Net[2] 0.8131 1.6352 2.7697 5.8040 0.4180 0.7404 1.0770 1.8165 0.4133 0.7448 1.1384 1.9151 LapSRN[18] 0.7644 2.3796 3.3389 6.1110 0.4443 0.9423 1.3430 1.9523 0.4300 0.9382 1.3388 2.0450 PDRN 0.6233 1.6634 2.6943 5.8083 0.3875 0.7313 1.0668 1.7323 0.3723 0.7347 1.0767 1.8567
下载: 导出CSV
表 3 数据集A上重建结果的定量评价(SSIM)
Table 3. Quantitative comparison (in SSIM) on dataset A
Art Books Moebius 2× 4× 8× 16× 2× 4× 8× 16× 2× 4× 8× 16× Bicubic 0.9868 0.9679 0.9433 0.9254 0.9956 0.9900 0.9835 0.9789 0.9950 0.9888 0.9811 0.9761 MRF[24] 0.9833 0.9749 0.9570 0.9371 0.9945 0.9916 0.9865 0.9811 0.9929 0.9901 0.9846 0.9792 Guided[4] 0.9830 0.9710 0.9579 0.9476 0.9945 0.9906 0.9865 0.9833 0.9934 0.9894 0.9853 0.9812 Edge[25] 0.9870 0.9797 0.9725 0.9605 0.9956 0.9918 0.9877 0.9846 0.9945 0.9910 0.9868 0.9840 TGV[3] 0.9858 0.9783 0.9668 0.9535 0.9945 0.9919 0.9886 0.9843 0.9941 0.9907 0.9860 0.9819 AP[27] 0.9952 0.9871 0.9798 0.9586 0.9961 0.9942 0.9909 0.9849 0.9972 0.9950 0.9906 0.9833 VDSR[15] 0.9964 0.9916 0.9801 0.9457 0.9985 0.9966 0.9932 0.9866 0.9980 0.9958 0.9913 0.9823 MS-Net[2] 0.9983 0.9941 0.9851 0.9557 0.9990 0.9973 0.9949 0.9894 0.9988 0.9965 0.9928 0.9851 LapSRN[18] 0.9984 0.9888 0.9791 0.9584 0.9986 0.9958 0.9931 0.9891 0.9986 0.9949 0.9912 0.9852 PDRN 0.9988 0.9945 0.9871 0.9601 0.9990 0.9971 0.9949 0.9898 0.9988 0.9965 0.9935 0.9863
下载: 导出CSV
表 4 数据集B上重建结果的定量评价(RMSE)
Table 4. Quantitative comparison (in RMSE) on dataset B
Dolls Laundry Reindeer 2× 4× 8× 16× 2× 4× 8× 16× 2× 4× 8× 16× Bicubic 0.9433 1.3356 1.8811 2.6451 1.6142 2.4077 3.4520 5.0923 1.9382 2.8086 3.9857 5.8591 Edge[25] 0.9713 1.3217 1.7750 2.4341 1.5525 2.1316 2.7698 4.1581 2.2674 2.4067 2.9873 4.2941 TGV[3] 1.1467 1.3869 1.8854 3.5878 1.9886 2.5115 3.7570 6.4066 2.4068 2.7115 3.7887 7.2711 AP[27] 1.1893 1.3888 1.6783 2.3456 1.7154 2.2553 2.8478 4.6564 1.8026 2.4309 2.9491 4.0877 SRCNN[13] 0.5814 0.9467 1.5185 2.4452 0.6353 1.1761 2.4306 4.5795 0.7658 1.4997 2.8643 5.2491 VDSR[15] 0.6308 0.8966 1.3148 2.0912 0.7249 1.1974 1.8392 3.2061 1.0051 1.5058 2.2814 4.1759 MS-Net[2] 0.4813 0.7835 1.2049 1.8627 0.4749 0.8842 1.6279 3.4353 0.5563 1.1068 1.9719 3.9215 LapSRN[18] 0.4942 1.0111 1.4194 1.9954 0.4617 1.3552 1.9314 2.5137 0.5075 1.7402 2.4538 3.0737 PDRN 0.4418 0.8317 1.1916 1.8230 0.3897 0.9240 1.4207 2.2084 0.4149 1.1047 1.7392 2.6655
下载: 导出CSV
表 5 数据集B上重建结果的定量评价(SSIM)
Table 5. Quantitative comparison (in SSIM) on dataset B
Dolls Laundry Reindeer 2× 4× 8× 16× 2× 4× 8× 16× 2× 4× 8× 16× Bicubic 0.9948 0.9893 0.9827 0.9783 0.9926 0.9833 0.9717 0.9635 0.9930 0.9846 0.9737 0.9642 Edge[25] 0.9950 0.9911 0.9876 0.9849 0.9938 0.9892 0.9850 0.9774 0.9897 0.9902 0.9863 0.9819 TGV[3] 0.9934 0.9902 0.9853 0.9770 0.9882 0.9820 0.9714 0.9551 0.9910 0.9874 0.9798 0.9690 AP[27] 0.9925 0.9901 0.9876 0.9842 0.9942 0.9905 0.9876 0.9757 0.9931 0.9891 0.9860 0.9794 VDSR[15] 0.9976 0.9953 0.9910 0.9457 0.9979 0.9835 0.9878 0.9762 0.9977 0.9953 0.9906 0.9773 MS-Net[2] 0.9987 0.9964 0.9921 0.9851 0.9989 0.9965 0.9899 0.9751 0.9989 0.9968 0.9929 0.9814 LapSRN[18] 0.9982 0.9941 0.9901 0.9851 0.9988 0.9942 0.9892 0.9858 0.9987 0.9938 0.9896 0.9868 PDRN 0.9985 0.9958 0.9922 0.9860 0.9990 0.9970 0.9937 0.9872 0.9990 0.9968 0.9942 0.9887
下载: 导出CSV
表 6 数据集C上重建结果的定量评价(RMSE/SSIM)
Table 6. Quantitative comparison (in RMSE/SSIM) on dataset C
Cones Teddy Tsukuba 2× 4× 2× 4× 2× 4× Bicubic 2.5422/0.9813 3.8666/0.9583 1.9610/0.9844 2.8583/0.9665 5.8201/0.9694 8.5638/0.9277 Edge[25] 2.8497/0.9699 6.5447/0.9420 2.1850/0.9767 4.3366/0.9553 6.8869/0.9320 12.123/0.8981 Ferstl[38] 2.1850/0.9866 3.4977/0.9645 1.6941/0.9884 2.5966/0.9716 5.3252/0.9766 7.5356/0.9413 Xie[39] 2.7338/0.9633 4.4087/0.9319 2.4911/0.9625 3.2768/0.9331 6.3534/0.9464 9.7765/0.8822 Song[40] 1.4356/0.9989 2.9789/0.9783 1.1974/0.9918 1.8006/0.9831 2.9841/0.9905 6.1422/0.9666 SRCNN[13] 1.4842/0.9965 3.5856/0.9672 1.1702/0.9923 1.9857/0.9820 3.2753/0.9879 7.9391/0.9587 VDSR[15] 1.7150/0.9917 2.9808/0.9797 1.2203/0.9925 1.8591/0.9836 3.7684/0.9896 5.9175/0.9686 MS-Net[2] 1.1005/0.9951 2.7659/0.9817 0.8204/0.9953 1.5283/0.9865 2.4536/0.9934 4.9927/0.9740 LapSRN[18] 1.0182/0.9958 3.1994/0.9755 0.8570/0.9951 2.0820/0.9802 2.0822/0.9960 6.2983/0.9649 PDRN 0.8556/0.9963 2.6049/0.9837 0.7359/0.9959 1.6421/0.9860 1.8128/0.9974 4.9136/0.9798
下载: 导出CSV
表 7 数据集D上重建结果的定量评价(RMSE/SSIM)
Table 7. Quantitative comparison (in RMSE/SSIM) on dataset D
Scan1 Scan2 Scan3 2× 4× 2× 4× 2× 4× Bicubic 4.2153/0.9864 6.4958/0.9689 3.4766/0.9873 5.2335/0.9734 4.0629/0.9865 6.4149/0.9658 Xie[39] - 9.1935/0.9781 - 7.4148/0.9791 - 8.9093/0.9680 VDSR[15] 2.7391/0.9911 3.9732/0.9865 2.2883/0.9919 3.2704/0.9878 1.4128/0.9960 3.0617/0.9912 MS-Net[2] 2.7502/0.9902 3.7618/0.9836 2.1329/0.9917 3.4159/0.9863 1.4296/0.9955 3.1048/0.9914 LapSRN[18] 2.3995/0.9913 4.2889/0.9834 1.9860/0.9920 3.5537/0.9852 1.4702/0.9957 3.6258/0.9878 PDRN 2.1698/0.9923 3.6122/0.9878 1.8003/0.9927 3.0407/0.9884 1.3034/0.9962 2.6953/0.9926
下载: 导出CSV
-
参考文献
[1] Ruiz-Sarmiento J R, Galindo C, Gonzalez J. Improving human face detection through TOF cameras for ambient intelligence applications[C]//Proceedings of the 2nd International Symposium on Ambient Intelligence, 2011: 125–132.
[2] Hui T W, Loy C C, Tang X O. Depth map super-resolution by deep multi-scale guidance[C]//Proceedings of the 14th European Conference on Computer Vision, 2016: 353–369.
[3] Ferstl D, Reinbacher C, Ranftl R, et al. Image guided depth upsampling using anisotropic total generalized variation[C]//Proceedings of 2013 IEEE International Conference on Computer Vision, 2013: 993–1000.
[4] He K M, Sun J, Tang X O. Guided image filtering[C]//Proceedings of the 11th European Conference on Computer Vision, 2010: 1–14.
[5] 汪荣贵, 汪庆辉, 杨娟, 等.融合特征分类和独立字典训练的超分辨率重建[J].光电工程, 2018, 45(1): 170542. doi: 10.12086/oee.2018.170542
Wang R G, Wang Q H, Yang J, et al. Image super-resolution reconstruction by fusing feature classification and independent dictionary training[J]. Opto-Electronic Engineering, 2018, 45(1): 170542. doi: 10.12086/oee.2018.170542
[6] 王飞, 王伟, 邱智亮.一种深度级联网络结构的单帧超分辨重建算法[J].光电工程, 2018, 45(7): 170729. doi: 10.12086/oee.2018.170729
Wang F, Wang W, Qiu Z L. A single super-resolution method via deep cascade network[J]. Opto-Electronic Engineering, 2018, 45(7): 170729. doi: 10.12086/oee.2018.170729
[7] Richardt C, Stoll C, Dodgson N A, et al. Coherent spatiotemporal filtering, upsampling and rendering of RGBZ videos[J]. Computer Graphics Forum, 2012, 31(2): 247–256. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1111/j.1467-8659.2012.03003.x
[8] Shen X Y, Zhou C, Xu L, et al. Mutual-structure for joint filtering[C]//Proceedings of 2015 IEEE International Conference on Computer Vision, 2015: 3406–3414.
[9] Kiechle M, Hawe S, Kleinsteuber M. A joint intensity and depth co-sparse analysis model for depth map super-resolution[C]//Proceedings of 2013 IEEE International Conference on Computer Vision, 2013: 1545–1552.
[10] Krizhevsky A, Sutskever I, Hinton G E. ImageNet classification with deep convolutional neural networks[C]//Proceedings of the 25th International Conference on Neural Information Processing Systems, 2012: 1097–1105.
[11] Ren S Q, He K M, Girshick R, et al. Faster R-CNN: towards real-time object detection with region proposal networks[C]//Proceedings of the 28th International Conference on Neural Information Processing Systems, 2015: 91–99.
[12] Long J, Shelhamer E, Darrell T. Fully convolutional networks for semantic segmentation[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2015: 3431–3440.
[13] Dong C, Loy C C, He K M, et al. Image super-resolution using deep convolutional networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(2): 295–307. doi: 10.1109/TPAMI.2015.2439281
[14] Wang Z W, Liu D, Yang J C, et al. Deep networks for image super-resolution with sparse prior[C]//Proceedings of IEEE International Conference on Computer Vision, 2015: 370–378.
[15] Kim J, Lee J K, Lee K M. Accurate image super-resolution using very deep convolutional networks[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition, 2016: 1646–1654.
[16] Huang G, Liu Z, Van Der Maaten L, et al. Densely connected convolutional networks[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition, 2017: 2261–2269.
[17] Shi W Z, Caballero J, Huszár F, et al. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition, 2016: 1874–1883.
[18] Lai W S, Huang J B, Ahuja N, et al. Deep laplacian pyramid networks for fast and accurate super-resolution[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017: 5835–5843.
[19] Kopf J, Cohen M F, Lischinski D, et al. Joint bilateral upsampling[J]. ACM Transactions on Graphics, 2007, 26(3): 96. doi: 10.1145/1276377.1276497
[20] Yang Q, Yang R, Davis J, et al. Spatial-depth super resolution for range images[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition, 2007: 1–8.
[21] Chan D, Buisman H, Theobalt C, et al. A noise-aware filter for real-time depth upsampling[C]//Proceedings of Workshop on Multi-camera and Multi-modal Sensor Fusion Algorithms and Applications, 2008.
[22] Lu J J, Forsyth D. Sparse depth super resolution[C]//Proceedings of 2005 IEEE Conference on Computer Vision and Pattern Recognition, 2015: 2245–2253.
[23] Yuan L, Jin X, Li Y G, et al. Depth map super-resolution via low-resolution depth guided joint trilateral up-sampling[J]. Journal of Visual Communication and Image Representation, 2017, 46: 280–291. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=c6a55a9af46e2364330e8d3bf0bac7ca
[24] Diebel J, Thrun S. An application of Markov random fields to range sensing[C]//Advances in Neural Information Processing Systems, 2005: 291–298.
[25] Park J, Kim H, Tai Y W, et al. High quality depth map upsampling for 3D-TOF cameras[C]//Proceedings of 2011 IEEE International Conference on Computer Vision, 2011: 1623–1630.
[26] Aodha O M, Campbell N D F, Nair A, et al. Patch based synthesis for single depth image super-resolution[C]//Proceedings of the 12th European Conference on Computer Vision, 2012: 71–84.
[27] Yang J Y, Ye X C, Li K, et al. Color-guided depth recovery from RGB-D data using an adaptive autoregressive model[J]. IEEE Transactions on Image Processing, 2014, 23(8): 3443–3458. doi: 10.1109/TIP.2014.2329776
[28] Lei J J, Li L L, Yue H J, et al. Depth map super-resolution considering view synthesis quality[J]. IEEE Transactions on Image Processing, 2017, 26(4): 1732–1745. doi: 10.1109/TIP.2017.2656463
[29] Denton E, Chintala S, Szlam A, et al. Deep generative image models using a Laplacian pyramid of adversarial networks[C]//Proceedings of the 28th International Conference on Neural Information Processing Systems, 2015: 1486–1494.
[30] He K M, Zhang X Y, Ren S Q, et al. Deep residual learning for image recognition[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition, 2016: 770–778.
[31] He K M, Zhang X Y, Ren S Q, et al. Delving deep into rectifiers: surpassing human-level performance on ImageNet classification[C]//Proceedings of 2015 IEEE International Conference on Computer Vision, 2015: 1026–1034.
[32] Scharstein D, Szeliski R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms[J]. International Journal of Computer Vision, 2002, 47(1–3): 7–42. http://d.old.wanfangdata.com.cn/NSTLQK/10.1364-JOSAB.28.002478/
[33] Scharstein D, Pal C. Learning conditional random fields for stereo[C]//Proceedings of 2007 IEEE Conference on Computer Vision and Pattern Recognition, 2007: 1–8.
[34] Scharstein D, Hirschmüller H, Kitajima Y, et al. High-resolution stereo datasets with subpixel-accurate ground truth[C]//Proceedings of the 36th German Conference on Pattern Recognition, 2014: 31–42.
[35] Handa A, Whelan T, McDonald J, et al. A benchmark for RGB-D visual odometry, 3D reconstruction and SLAM[C]//Proceedings of 2014 IEEE International Conference on Robotics and Automation, 2014: 1524–1531.
[36] Glorot X, Bengio Y. Understanding the difficulty of training deep feedforward neural networks[C]//Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, 2010: 249–256.
[37] Kingma D, Ba J. Adam: a method for stochastic optimization[C]//Proceedings of the 3rd International Conference on Learning Representations, 2014.
[38] Ferstl D, Rüther M, Bischof H. Variational depth superresolution using example-based edge representations[C]//Proceedings of 2015 IEEE International Conference on Computer Vision, 2015: 513–521.
[39] Xie J, Feris R S, Sun M T. Edge guided single depth image super resolution[C]//Proceedings of 2014 IEEE International Conference on Image Processing, 2014: 3773–3777.
[40] Song X B, Dai Y C, Qin X Y. Deep depth super-resolution: learning depth super-resolution using deep convolutional neural network[C]//Proceedings of the 13th Asian Conference on Computer Vision, 2017: 360–376.
-
访问统计
点击扫一扫
图(8)
表(8)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
