E-mail Alert
RSS
-
摘要
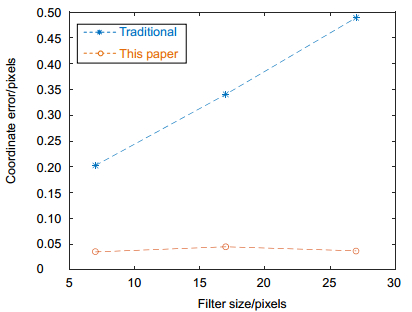
现阶段通用的相机标定方法需要使用者提供准确的标定板特征点像素坐标。但对某些成像位置特殊的相机而言，一般标定物(如长宽在厘米级别的标定板)的使用范围在其清晰成像范围之外。使用这些相机拍摄一般标定物，只能得到离焦的模糊图像，无法准确提取特征点像素坐标。本文分析了光学系统离焦状态对基于正弦光栅的结构光(简称正弦结构光)相位的影响。利用正弦结构光相位与相机对焦状态无关的性质，提出了一种利用相移法正弦结构光编码的方法，对标定物上特征点进行相位编码，实现了相机在离焦状态下的标定。经过实验验证，标定结果焦距长度与真实值之间最大偏差为0.47%，最大像素重投影误差为0.17 pixels。该方法为具有特殊成像范围的相机的标定提供了一种解决方案。
Abstract
The state-of-art camera calibration method requires the user to provide accurate pixel coordinates of calibration plate feature points. For some cameras with special sensing range, general calibration objects' (such as calibration plates with a centimeter-long dimension) using range is outside their clear sensing range. Using these cameras to take a picture for general calibration objects, you can only get out-of-focused blurred images that can not accurately extract feature points' pixel coordinates. This paper analyzes the influence on the phase of the structured light based on sine grating (abbreviated as sinusoidal structured light) when optical system is in defocus state. Based on the fact that the state of focus is independent of the phase of sinusoidal structured light, a method of phase-shifted sinusoidal structured light encoding by phase shift is proposed to encode the feature points on the calibration object and this method realizes the calibration of the camera under out-of-focus condition. The experimental results show that the maximal deviation of focal length from the real value is 0.47% and the maximal pixel reprojection error is 0.17 pixels. This paper provides a solution to camera calibration with a special sensing range.
-
Key words:
- calibration /
- focusing /
- phase matching /
- phase shift /
- photographic equipment
-
Overview
Overview: With development in the past decades, the normal camera calibration method has become more and more mature. Among them, the method proposed by Zhang is a representative one. However, there is still a lack of the calibration method of some cameras and lenses used in special occasions. Recently, there are a few calibration studies for cameras with special imaging ranges, such as macro cameras and telephoto cameras. In 2012, Guo proposed a method for macro camera calibration using a semicircle template instead of a checkerboard in the general method. This method needs to fit the semicircle curve during the actual use. This step is difficult in the use of this method. Wang proposed a calibration pattern that can still be detected when the camera is out of focus, but its rendering method is difficult.
Our works are as follows: The state-of-art camera calibration method requires the user to provide accurate pixel coordinate of calibration plate feature points. For some cameras with special sensing range, general calibration objects' (such as calibration plates with a centimeter-long dimension) using range is outside their clear sensing range. This paper analyzes the influence of the focusing state of the camera imaging system on the optical phase information of a sinusoidal structured light. Using the properties that the sinusoidal structured light's phase information is independent of the focusing state of the camera, this paper proposes a method for encoding a normal calibration object using sinusoidal structured light to make the calibration of the camera in the defocus state make true. This method uses an in-focus camera to get the phase information of the encoded normal calibration object. The out-of-focus camera uses the phase information to calculate the feature points' accurate coordinates by the phase information. Then, the traditional method (e.g. Zhang method) is used to calculate the intrinsic, extrinsic parameters and distortion coefficient of the out-of-focus camera. Based on this method, the camera parameters can be accurately calibrated by using a blurred picture of the coded calibration object. This paper provides a cheap and convenient solution to the calibration of these special cameras. We don't have to manufacture the special calibration objects. The experiment results show that this method can calibrate special camera parameters accurately under different defocus state. After experimental verification, the calibrated focal length deviation from the real value is 0.47%, the average pixel reprojection error is 0.17 pixels.
-
-
图 1 正弦结构光图案及正弦结构光与背景光叠加后频谱。(a)正弦结构光图案；(b)正弦结构光与背景光叠加后频谱
Figure 1. Pattern of sinusoidal structured light and the spectrum diagram of sinusoidal structured light and background light's superposition. (a) Pattern of sinusoidal structured light; (b) The spectrum diagram of sinusoidal structured light and background light's superposition
图 6 对焦相机获得的图像。(a)对焦相机获得的标定板图像；(b)从6(a)中提取到的圆心
Figure 6. The image obtained by the in-focus camera. (a) The calibration plate's image obtained by the in-focus camera; (b) The circle centers extracted from 6(a)
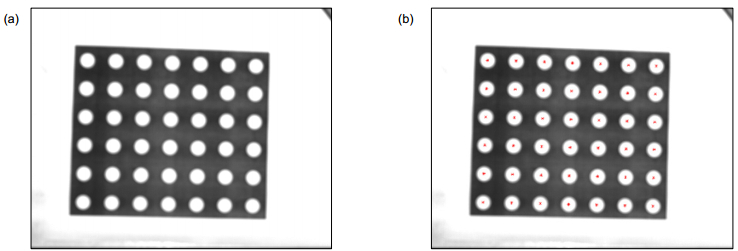
图 7 编码后的标定板图像。(a)对焦相机得到的水平结构光图像；(b)对焦相机得到的垂直结构光图像；(c)离焦相机得到的水平结构光图像；(d)离焦相机得到的垂直结构光图像
Figure 7. The images of encoded calibration board. (a) The horizontal structured light image obtained by in-focus camera; (b) The vertical structured light image obtained by in-focus camera; (c) The horizontal structured light image obtained by out-of-focus camera; (d) The vertical structured light image obtained by out-of-focus camera
图 8 离焦图像的所有圆心位置。(a) 离焦相机获得的标定板模糊图片；(b) 模糊图片圆心
Figure 8. All of the circle centers’ positions of the blurred image. (a) The blurred calibration plate image obtained by the out-of-focus camera; (b) The centers of the blurred image
表 1 不同标定距离下的相机内参数
Table 1. Intrinsic camera parameters at different calibration distances
Distance/m α β γ u0 v0 Reprojection error/pixel 0.5 3105.86 3108.37 0.60 636.73 543.17 0.16 1 3096.71 3097.91 0.47 638.12 541.21 0.17 2 3094.87 3095.40 0.02 628.66 542.26 0.17 
下载: 导出CSV
表 2 不同距离下的相机畸变参数
Table 2. Distortion parameters at different calibration distances
Distance/m k1 k2 k3 p1 p2 0.5 -0.1736 4.7222 -92.7816 0.0013 -0.0017 1 -0.1285 2.8493 -44.4313 0.0013 -0.0019 2 -0.1603 3.1751 -72.6934 0.0011 -0.0021
下载: 导出CSV
表 3 标定得到的焦距
Table 3. Calibrated focal length
Distance/m Focal length/mm Error/% 0.5 16.157 0.43 1 16.106 0.12 2 16.094 0.04
下载: 导出CSV
-
参考文献
[1] Salvi J, Armangué X, Batlle J. A comparative review of camera calibrating methods with accuracy evaluation[J]. Pattern recognition, 2002, 35(7): 1617–1635. doi: 10.1016/S0031-3203(01)00126-1
[2] 邱茂林, 马颂德, 李毅.计算机视觉中摄像机定标综述[J].自动化学报, 2000, 26(1): 43–55. http://d.wanfangdata.com.cn/Periodical_zdhxb200001006.aspx
Qiu M L, Ma S D, Li Y. Overview of camera calibration for computer vision[J]. Acta Automatica Sinica, 2000, 26(1): 43–55. http://d.wanfangdata.com.cn/Periodical_zdhxb200001006.aspx
[3] Abdel-Aziz Y I, Karara H M, Hauck M. Direct linear transformation from comparator coordinates into object space coordinates in close-range photogrammetry[J]. Photogrammetric Engineering & Remote Sensing, 2015, 81(2):103–107. http://cn.bing.com/academic/profile?id=2dc5bfac9356f628a430ee9ca1d6ff70&encoded=0&v=paper_preview&mkt=zh-cn
[4] Faig W. Calibration of close-range photogrammetry systems: Mathematical formulation[J]. Photogrammetric Engineering and Remote Sensing, 1975, 41(12): 1479–1486. http://www.isprs.org/proceedings/XXXVII/congress/5_pdf/22.pdf
[5] Tsai R. A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses[J]. IEEE Journal on Robotics and Automation, 1987, 3(4): 323–344. doi: 10.1109/JRA.1987.1087109
[6] Zhang Z. A flexible new technique for camera calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330–1334. doi: 10.1109/34.888718
[7] 郭涛, 达飞鹏, 方旭.小视场环境下的摄像机标定[J].中国激光, 2012, 39(8): 164–168. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2707585
Guo T, Da F P, Fang X. Camera calibration under small field of view[J]. Chinese Journal of Lasers, 2012, 39(8): 164–168 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2707585
[8] Wang Y W, Chen X C, Tao J Y, et al. Accurate feature detection for out-of-focus camera calibration[J]. Applied Optics, 2016, 55(28): 7964–7971. doi: 10.1364/AO.55.007964
[9] Szeliski R. Computer vision: algorithms and applications[M]. New York: Springer, 2010: 45–51.
[10] 石爱军, 白瑞林, 田青华. Gray码结合线移的结构光三维测量[J].光电工程, 2016, 43(11): 26–32. doi: 10.3969/j.issn.1003-501X.2016.11.005
Shi A J, Bai R L, Tian Q H. 3D measurement based on structured light using a combination of Gray code and line-shift patterns[J]. Opto-Electronic Engineering, 2016, 43(11): 26–32. doi: 10.3969/j.issn.1003-501X.2016.11.005
[11] 林俊义, 黄剑清, 江开勇.分区域Gamma预编码校正的相位误差补偿[J].光电工程, 2016, 43(9): 32–38. http://mall.cnki.net/magazine/Article/GDGC201609007.htm
Lin J Y, Huang J Q, Jiang K Y. Subregional Gamma pre-coding correction for phase error compensation[J]. Opto-Electronic Engineering, 2016, 43(9): 32–38. http://mall.cnki.net/magazine/Article/GDGC201609007.htm
[12] 张万祯. 数字投影结构光三维测量方法研究[D]. 杭州: 浙江大学, 2015.
Zhang W Z. Structured-light three dimensional measurement method based on digital projector[D]. Hangzhou: Zhejiang University, 2015.
[13] Li B W, Karpinsky N, Zhang S. Novel calibration method for structured-light system with an out-of-focus projector[J]. Applied Optics, 2014, 53(16): 3415–3426. doi: 10.1364/AO.53.003415
-
访问统计
点击扫一扫
图(8)
表(3)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
