-
摘要
分数傅里叶变换是傅里叶变换的广义形式,提供了介于时域和频域之间的多分数域信号表征,为非平稳信号处理和线性时变系统分析开辟了新途径,应用十分广泛。本文首先总结近年来分数傅里叶变换的理论研究成果,包括分数傅里叶变换的数值计算、衍生的离散分数变换、分数域采样、分数域滤波与参数估计、多分数域分析。然后介绍分数傅里叶变换在工程和实践中的应用,包括雷达、通信、图像加密、光学干涉测量、医学、生物、机械仪器等。最后对分数傅里叶变换理论及其应用的未来研究方向进行展望。
Abstract
The fractional Fourier transform (FRFT) is a generalization of the Fourier transform. The FRFT can characterize signals in multiple fractional domains and provide new perspectives for non-stationary signal processing and linear time variant system analysis, thus it is widely used in reality applications. We first review recent developments of the FRFT in theory, including discretization algorithms of the FRFT, various discrete fractional transforms, sampling theorems in fractional domains, filtering and parameter estimation in fractional domains, joint analysis in multiple fractional domains. Then we summarize various applications of the FRFT, including radar and communication signal processing in fractional domains, image encryption, optical interference measurement, medicine, biology, and instrument signal processing based on the FRFT. Finally we discuss the future research directions of the FRFT, including fast algorithm of the FRFT, sparse sampling in fractional domains, machine learning utilizing the FRFT, graph signal processing in fractional domains, and discrete FRFT based on quantum computation.
-
Overview

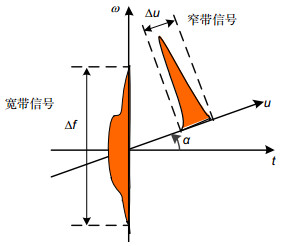
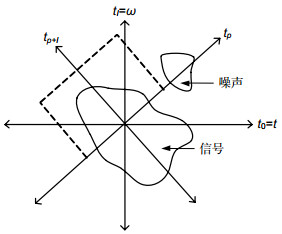
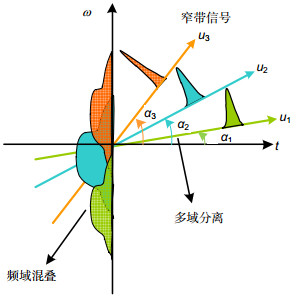
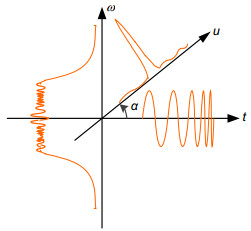
Overview:The fractional Fourier transform (FRFT) is a generalization of the Fourier transform. It has been received much attention since Namias provided its definition in the perspective of eigendecomposition and its application in quantum in 1980. FRFT can be interpreted as decomposition of a signal into chirp signals or rotation of the time-frequency plane with angle α. After years of research, the theoretical system of the FRFT has been relatively completed. Efficient and accurate discretization algorithms and sampling theorem associated with the FRFT make the digital signal processing based on discrete FRFT possible. Filtering and parameter estimation in fractional domains greatly promote applications of the FRFT in practice. Analysis of a signal in multiple fractional domains jointly distinguish signal processing utilizing FRFT from traditional signal processing, this is because with the rotation angle α changing from 0 to π/2, the FRFT of a signal can provide characteristics of the signal in many fractional domains, including time domain and frequency domain. Meanwhile, with the development of theoretical research, the FRFT also shows great values in practice. In addition to traditional areas such as quantum and optical, FRFT has also been applied in the area of signal processing, especially in radar signal processing, communication signal processing, image processing, medical signal processing, biology signal processing, and mechanical signal processing, et al. In this paper, we first provide definitions of the FRFT and its basic properties. We then review recent developments of the FRFT in theory, including discretization algorithms of the FRFT, various discrete fractional transforms derived from the discrete FRFT, sampling theory associated with the FRFT, filtering and parameter estimation in fractional domains, and joint analysis in multiple fractional domains. We next summarize progress in several application areas utilizing FRFT, including radar, communication, image encryption, optical measurement, health care, biology, and instrument. We also provide several future research directions of the FRFT, for example, fast algorithm and sparse sampling associated with the FRFT can be studied further to reduce complexity, existing applications of the FRFT can be promoted to improve the system performance further, FRFT can also be applied to machine learning because FRFT can provide characteristic of images in multiple fractional domains, FRFT based on graph may be very useful in graph signal processing, and discrete FRFT based on quantum computation may greatly reduce the complexity. By summarizing the research history, presenting research focus, and discussing future research directions of the FRFT, we try to provide a relatively comprehensive overview to the research progress in the FRFT to help readers to understand this filed better.
-

-
表 1 离散分数傅里叶变换特征值及其分配规则[30]
Table 1. Eigenvalues and their assignment rule of the discrete fractional Fourier transform (DFRFT) matrix[30]
N 离散分数傅里叶变换的特征值 4m exp(-ikα), k=0, 1, …, 4m-2, 4m 4m+1 exp(-ikα), k=0, 1, …, 4m-1, 4m 4m+2 exp(-ikα), k=0, 1, …, 4m, 4m+2 4m+3 exp(-ikα), k=0, 1, …, 4m+1, 4m+2 表 2 离散分数傅里叶变换算法的性质比较
Table 2. Comparison of the properties of DFRFT algorithms
酉性 阶次可加性 可逆性 逼近连续FRFT 闭合式 计算复杂度 Ozaktas采样型 × × × √ × O(N·log2N) Pei采样型 √ × √ √ √ O(N·log2N) 特征分解型 √ √ √ √ × O(N2) -
参考文献
[1] Wiener N. Hermitian polynomials and Fourier analysis[J]. Journal of Mathematics and Physics, 1929, 8(1-4):70-73. doi: 10.1002/sapm19298170
[2] Namias V. The fractional order Fourier transform and its application to quantum mechanics[J]. IMA Journal of Applied Mathematics, 1980, 25(3):241-265. doi: 10.1093/imamat/25.3.241
[3] McBride A C, Kerr F H. On namias's fractional Fourier transforms[J]. IMA Journal of Applied Mathematics, 1987, 39(2):159-175. doi: 10.1093/imamat/39.2.159
[4] Mendlovic D, Ozaktas H M. Fractional Fourier transforms and their optical implementation:I[J]. Journal of the Optical Society of America A, 1993, 10(9):1875-1881. doi: 10.1364/JOSAA.10.001875
[5] Ozaktas H M, Mendlovic D. Fractional Fourier transforms and their optical implementation. Ⅱ[J]. Journal of the Optical Society of America A, 1993, 10(12):2522-2531. doi: 10.1364/JOSAA.10.002522
[6] 康学净. 离散分数变换及其在图像加密中的应用[D]. 北京: 北京理工大学, 2016.
Kang X J. Discrete fractional transforms and their applications to image encryption[D]. Beijing: Beijing Institute of Technology, 2016.
[7] Almeida L B. The fractional Fourier transform and time-frequency representations[J]. IEEE Transactions on Signal Processing, 1994, 42(11):3084-3091. doi: 10.1109/78.330368
[8] Ozaktas H M, Barshan B, Onural L, et al. Filtering in fractional Fourier domains and their relation to Chirp transforms[C]//Proceedings of the 7th Mediterranean Electrotechnical Conference, 1994: 77-79.
[9] Zayed A I. On the relationship between the Fourier and fractional Fourier transforms[J]. IEEE Signal Processing Letters, 1996, 3(12):310-311. doi: 10.1109/97.544785
[10] Cariolaro G, Erseghe T, Kraniauskas P, et al. A unified framework for the fractional Fourier transform[J]. IEEE Transactions on Signal Processing, 1998, 46(12):3206-3219. doi: 10.1109/78.735297
[11] Tao R, Deng B, Wang Y. Research progress of the fractional Fourier transform in signal processing[J]. Science in China Series F: Information Sciences, 2006, 49(1):1-25. doi: 10.1007/s11432-005-0240-y
[12] Tao R, Zhang F, Wang Y. Research progress on discretization of fractional Fourier transform[J]. Science in China Series F: Information Sciences, 2008, 51(7):859-880. doi: 10.1007/s11432-008-0069-2
[13] Sejdić E, Djurović I, Stanković L. Fractional Fourier transform as a signal processing tool:an overview of recent developments[J]. Signal Processing, 2011, 91(6):1351-1369. doi: 10.1016/j.sigpro.2010.10.008
[14] Saxena R, Singh K. Fractional Fourier transform:a novel tool for signal processing[J]. Journal of the Indian Institute of Science, 2005, 85:11-26. https://www.wenkuxiazai.com/doc/0d0707d4240c844769eaee6f-2.html
[15] Zhang Y D, Wang S H, Yang J F, et al. A comprehensive survey on fractional Fourier transform[J]. Fundamenta Informaticae, 2017, 151(1-4):1-48. doi: 10.3233/FI-2017-1477
[16] 陶然, 邓兵, 王越.分数阶傅里叶变换及其应用[M].北京:清华大学出版社, 2009.
Tao R, Deng B, Wang Y. Fractional Fourier Transform and Its Applications[M]. Beijing:Tsinghua University Press, 2009.
[17] Ozaktas H M, Zalevsky Z, Kutay M A. The Fractional Fourier Transform: with Applications in Optics and Signal Processing [M]. New York:Wiley, 2001.
[18] Ozaktas H M, Barshan B, Mendlovic D, et al. Convolution, filtering, and multiplexing in fractional Fourier domains and their relation to Chirp and wavelet transforms[J]. Journal of the Optical Society of America A, 1994, 11(2):547-559. doi: 10.1364/JOSAA.11.000547
[19] Pei S C, Ding J J. Relations between Gabor transforms and fractional Fourier transforms and their applications for signal processing[J]. IEEE Transactions on Signal Processing, 2007, 55(10):4839-4850. doi: 10.1109/TSP.2007.896271
[20] Pendry J B. Negative refraction makes a perfect lens[J]. Physical Review Letters, 2000, 85(18):3966-3969. doi: 10.1103/PhysRevLett.85.3966
[21] Richman M S, Parks T W. Understanding discrete rotations[C]//Proceedings of 1997 IEEE International Conference on Acoustics, Speech, and Signal Processing, 1997, 3: 2057-2060.
https://www.researchgate.net/publication/2722155_Understanding_Discrete_Rotations [22] Deng X G, Li Y P, Fan D Y, et al. A fast algorithm for fractional Fourier transforms[J]. Optics Communications, 1997, 138(4-6):270-274. doi: 10.1016/S0030-4018(97)00057-6
[23] Ikram M Z, Abed-Meraim K, Hua Y B. Fast quadratic phase transform for estimating the parameters of multicomponent Chirp signals[J]. Digital Signal Processing, 1997, 7(2):127-135. doi: 10.1006/dspr.1997.0286
[24] Bi G A, Wei Y M, Li G, et al. Radix-2 DIF fast algorithms for polynomial time-frequency transforms[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(4):1540-1546. doi: 10.1109/TAES.2006.314595
[25] Ju Y T, Bi G A. Generalized fast algorithms for the polynomial time-frequency transform[J]. IEEE Transactions on Signal Processing, 2007, 55(10):4907-4915. doi: 10.1109/TSP.2007.896102
[26] Bi G A, Ju Y T, Li X M. Fast algorithms for polynomial time-frequency transforms of real-valued sequences[J]. IEEE Transactions on Signal Processing, 2008, 56(5):1905-1915. doi: 10.1109/TSP.2007.913162
[27] Ozaktas H M, Arikan O, Kutay M A, et al. Digital computation of the fractional Fourier transform[J]. IEEE Transactions on Signal Processing, 1996, 44(9):2141-2150. doi: 10.1109/78.536672
[28] Pei S C, Ding J J. Closed-form discrete fractional and affine Fourier transforms[J]. IEEE Transactions on Signal Processing, 2000, 48(5):1338-1353. doi: 10.1109/78.839981
[29] Dickinson B W, Steiglitz K. Eigenvectors and functions of the discrete Fourier transform[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1982, 30(1):25-31. doi: 10.1109/TASSP.1982.1163843
[30] Pei S C, Yeh M H. Improved discrete fractional Fourier transform[J]. Optics Letters, 1997, 22(14):1047-1049. doi: 10.1364/OL.22.001047
[31] Pei S C, Yeh M H, Tseng C C. Discrete fractional Fourier transform based on orthogonal projections[J]. IEEE Transactions on Signal Processing, 1999, 47(5):1335-1348. doi: 10.1109/78.757221
[32] Pei S C, Hsue W L, Ding J J. Discrete fractional Fourier transform based on new nearly tridiagonal commuting matrices[J]. IEEE Transactions on Signal Processing, 2006, 54(10):3815-3828. doi: 10.1109/TSP.2006.879313
[33] Candan C. On higher order approximations for Hermite-Gaussian functions and discrete fractional Fourier transforms[J]. IEEE Signal Processing Letters, 2007, 14(10):699-702. doi: 10.1109/LSP.2007.898354
[34] Pei S C, Hsue W L, Ding J J. DFT-commuting matrix with arbitrary or infinite order second derivative approximation[J]. IEEE Transactions on Signal Processing, 2009, 57(1):390-394. doi: 10.1109/TSP.2008.2007927
[35] Serbes A, Durak-Ata L. Efficient computation of DFT commuting matrices by a closed-form infinite order approximation to the second differentiation matrix[J]. Signal Processing, 2011, 91(3):582-589. doi: 10.1016/j.sigpro.2010.05.002
[36] Pei S C, Tseng C C, Yeh M H. A new discrete fractional Fourier transform based on constrained eigendecomposition of DFT matrix by Lagrange multiplier method[J]. IEEE Transactions on Circuits and Systems Ⅱ: Analog and Digital Signal Processing, 1999, 46(9):1240-1245. doi: 10.1109/82.793715
[37] Candan C, Kutay M A, Ozaktas H M. The discrete fractional Fourier transform[J]. IEEE Transactions on Signal Processing, 2000, 48(5):1329-1337. doi: 10.1109/78.839980
[38] Candan C. On the eigenstructure of DFT matrices[DSP education][J]. IEEE Signal Processing Magazine, 2011, 28(2):105-108. doi: 10.1109/MSP.2010.940004
[39] Serbes A, Durak-Ata L. The discrete fractional Fourier transform based on the DFT matrix[J]. Signal Processing, 2011, 91(3):571-581. doi: 10.1016/j.sigpro.2010.05.007
[40] Hanna M T. The direct batch generation of Hermite-Gaussian-like eigenvectors of the DFT matrix using the notion of matrix pseudoinverse[C]//Proceedings of 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, 2013: 6063-6067.
https://ieeexplore.ieee.org/document/6638829/ [41] De Oliveira Neto J R, Lima J B. Discrete fractional Fourier transforms based on closed-form Hermite-Gaussian-like DFT eigenvectors[J]. IEEE Transactions on Signal Processing, 2017, 65(23):6171-6184. doi: 10.1109/TSP.2017.2750105
[42] Qi L, Tao R, Zhou S Y, et al. Detection and parameter estimation of multicomponent LFM signal based on the fractional Fourier transform[J]. Science in China Series F: Information Sciences, 2004, 47(2):184-198. doi: 10.1360/02yf0456
[43] Sui L S, Xin M T, Tian A L. Multiple-image encryption based on phase mask multiplexing in fractional Fourier transform domain[J]. Optics Letters, 2013, 38(11):1996-1998. doi: 10.1364/OL.38.001996
[44] Wang Q, Guo Q, Lei L, et al. Iterative partial phase encoding based on joint fractional Fourier transform correlator adopting phase-shifting digital holography[J]. Optics Communications, 2014, 313:1-8. doi: 10.1016/j.optcom.2013.09.058
[45] Zhu B H, Liu S T, Ran Q W. Optical image encryption based on multifractional Fourier transforms[J]. Optics Letters, 2000, 25(16):1159-1161. doi: 10.1364/OL.25.001159
[46] Pei S C, Tseng C C, Yeh M H, et al. Discrete fractional Hartley and Fourier transforms[J]. IEEE Transactions on Circuits and Systems Ⅱ: Analog and Digital Signal Processing, 1998, 45(6):665-675. doi: 10.1109/82.686685
[47] Santhanam B, McClellan J H. The discrete rotational Fourier transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4):994-998. doi: 10.1109/78.492554
[48] Pei S C, Yeh M H. The discrete fractional cosine and sine transforms[J]. IEEE Transactions on Signal Processing, 2001, 49(6):1198-1207. doi: 10.1109/78.923302
[49] Pei S C, Ding J J. Fractional cosine, sine, and Hartley transforms[J]. IEEE Transactions on Signal Processing, 2002, 50(7) 1661-1680. doi: 10.1109/TSP.2002.1011207
[50] Tseng C C. Eigenvalues and eigenvectors of generalized DFT, generalized DHT, DCT-Ⅳ and DST-Ⅳ matrices[J]. IEEE Transactions on Signal Processing, 2002, 50(4):866-877. doi: 10.1109/78.992133
[51] Erseghe T, Cariolaro G. Efficient DFT architectures based upon symmetries[J]. IEEE Transactions on Signal Processing, 2006, 54(10):3829-3838. doi: 10.1109/TSP.2006.880216
[52] Pei S C, Hsue W L. Tridiagonal commuting matrices and fractionalizations of DCT and DST matrices of types Ⅰ, Ⅳ, Ⅴ, and Ⅷ[J]. IEEE Transactions on Signal Processing, 2008, 56(6):2357-2369. doi: 10.1109/TSP.2007.914351
[53] Wei D Y, Li Y M. Novel tridiagonal commuting matrices for types Ⅰ, Ⅳ, Ⅴ, Ⅷ DCT and DST matrices[J]. IEEE Signal Processing Letters, 2014, 21(4):483-487. doi: 10.1109/LSP.2014.2306996
[54] Lohmann A W, Mendlovic D, Zalevsky Z. Fractional Hilbert transform[J]. Optics Letters, 1996, 21(4):281-283. doi: 10.1364/OL.21.000281
[55] Davis J A, McNamara D E, Cottrell D M. Analysis of the fractional Hilbert transform[J]. Applied Optics, 1998, 37(29):6911-6913. doi: 10.1364/AO.37.006911
[56] Pei S C, Yeh M H. Discrete fractional Hilbert transform[J]. IEEE Transactions on Circuits and Systems Ⅱ: Analog and Digital Signal Processing, 2000, 47(11):1307-1311. doi: 10.1109/82.885138
[57] Tseng C C, Pei S C. Design and application of discrete-time fractional Hilbert transformer[J]. IEEE Transactions on Circuits and Systems Ⅱ: Analog and Digital Signal Processing, 2000, 47(12):1529-1533. doi: 10.1109/82.899647
[58] Tao R, Li X M, Wang Y. Generalization of the fractional Hilbert transform[J]. IEEE Signal Processing Letters, 2008, 15:365-368. doi: 10.1109/LSP.2008.919814
[59] Hsue W L, Pei S C. The multiple-parameter discrete fractional Fourier transform and its application[C]//Proceedings of 2006 IEEE International Conference on Acoustics, Speech and Signal Processing, 2006, 3: 2867-2870.
https://ieeexplore.ieee.org/document/1660679/ [60] Pei S C, Hsue W L. The multiple-parameter discrete fractional Fourier transform[J]. IEEE Signal Processing Letters, 2006, 13(6):329-332. doi: 10.1109/LSP.2006.871721
[61] Lang J, Tao R, Ran Q W, et al. The multiple-parameter fractional Fourier transform[J]. Science in China Series F: Information Sciences, 2008, 51(8):1010-1024. doi: 10.1007/s11432-008-0073-6
[62] Lang J, Tao R, Wang Y. The discrete multiple-parameter fractional Fourier transform[J]. Science China Information Sciences, 2010, 53(11):2287-2299. doi: 10.1007/s11432-010-4095-5
[63] Ran Q W, Zhang H Y, Zhang J, et al. Deficiencies of the cryptography based on multiple-parameter fractional Fourier transform[J]. Optics Letters, 2009, 34(11):1729-1731. doi: 10.1364/OL.34.001729
[64] Lang J. The reality-preserving multiple-parameter fractional Fourier transform and its application to image encryption[C]//Proceedings of the 2012 5th International Congress on Image and Signal Processing, 2012: 1153-1157.
https://ieeexplore.ieee.org/document/6469747/ [65] Kang X J, Tao R, Zhang F. Multiple-parameter discrete fractional transform and its applications[J]. IEEE Transactions on Signal Processing, 2016, 64(13):3402-3417. doi: 10.1109/TSP.2016.2544740
[66] Liu Z J, Zhao H F, Liu S T. A discrete fractional random transform[J]. Optics Communications, 2005, 255(4-6):357-365. doi: 10.1016/j.optcom.2005.06.031
[67] Liu Z J, Guo Q, Liu S T. The discrete fractional random cosine and sine transforms[J]. Optics Communications, 2006, 265(1):100-105. doi: 10.1016/j.optcom.2006.03.010
[68] Liu Z J, Liu S T. Random fractional Fourier transform[J]. Optics Letters, 2007, 32(15):2088-2090. doi: 10.1364/OL.32.002088
[69] Pei S C, Hsue W L. Random discrete fractional Fourier transform[J]. IEEE Signal Processing Letters, 2009, 16(12):1015-1018. doi: 10.1109/LSP.2009.2027646
[70] Kang X J, Zhang F, Tao R. Multichannel random discrete fractional Fourier transform[J]. IEEE Signal Processing Letters, 2015, 22(9):1340-1344. doi: 10.1109/LSP.2015.2402395
[71] Pei S C, Yeh M H. Discrete fractional Hadamard transform[C]//Proceedings of 1999 IEEE International Symposium on Circuits and Systems, 1999, 3: 179-182.
https://pdfs.semanticscholar.org/ce82/63d0914f2caa5ad043668776a2660db257ca.pdf [72] Tseng C C. Eigenvector and fractionalization of discrete Hadamard transform[C]//Proceedings of 2007 IEEE International Symposium on Circuits and Systems, 2007, 2307-2310.
https://www.researchgate.net/publication/224714747_Eigenvector_and_Fractionalization_of_Discrete_Hadamard_Transform [73] Tao R, Lang J, Wang Y. The multiple-parameter discrete fractional Hadamard transform[J]. Optics Communications, 2009, 282(8):1531-1535. doi: 10.1016/j.optcom.2008.12.070
[74] Liu Z J, Ahmad M A, Liu S T. A discrete fractional angular transform[J]. Optics Communications, 2008, 281(6):1424- 1429. doi: 10.1016/j.optcom.2007.11.012
[75] Lammers M. The finite fractional Zak transform[J]. IEEE Signal Processing Letters, 2014, 21(9):1064-1067. doi: 10.1109/LSP.2014.2324495
[76] Ran Q W, Yeung D S, Tsang E C C, et al. General multifractional Fourier transform method based on the generalized permutation matrix group[J]. IEEE Transactions on Signal Processing, 2005, 53(1):83-98. doi: 10.1109/TSP.2004.837397
[77] Xia X G. On bandlimited signals with fractional Fourier transform[J]. IEEE Signal Processing Letters, 1996, 3(3):72-74. doi: 10.1109/97.481159
[78] Candan Ç, Ozaktas H M. Sampling and series expansion theorems for fractional Fourier and other transforms[J]. Signal Processing, 2003, 83(11):2455-2457. doi: 10.1016/S0165-1684(03)00196-8
[79] Erseghe T, Kraniauskas P, Carioraro G. Unified fractional Fourier transform and sampling theorem[J]. IEEE Transactions on Signal Processing, 1999, 47(12):3419-3423. http://cn.bing.com/academic/profile?id=0eb1430acf11add809e9b031f9fa1f74&encoded=0&v=paper_preview&mkt=zh-cn
[80] Wei D Y, Ran Q W, Li Y M. Sampling of fractional bandlimited signals associated with fractional Fourier transform[J]. Optik-International Journal for Light and Electron Optics, 2012, 123(2):137-139. doi: 10.1016/j.ijleo.2011.02.024
[81] Deng B, Tao R, Wang Y. Convolution theorems for the linear canonical transform and their applications[J]. Science in China Series F: Information Sciences, 2006, 49(5):592-603. doi: 10.1007/s11432-006-2016-4
[82] Meng X Y, Tao R, Wang Y. Fractional Fourier domain analysis of decimation and interpolation[J]. Science in China Series F: Information Sciences, 2007, 50(4):521-538. doi: 10.1007/s11432-007-0040-7
[83] Tao R, Deng B, Zhang W Q, et al. Sampling and sampling rate conversion of band limited signals in the fractional Fourier transform domain[J]. IEEE Transactions on Signal Processing, 2008, 56(1):158-171. doi: 10.1109/TSP.2007.901666
[84] Zhao J, Tao R, Wang Y. Sampling rate conversion for linear canonical transform[J]. Signal Processing, 2008, 88(11):2825- 2832. doi: 10.1016/j.sigpro.2008.06.008
[85] Zayed A I, Garcı́a A G. New sampling formulae for the fractional Fourier transform[J]. Signal Processing, 1999, 77(1):111-114. doi: 10.1016/S0165-1684(99)00064-X
[86] Li B Z, Tao R, Wang Y. New sampling formulae related to linear canonical transform[J]. Signal Processing, 2007, 87(5):983- 990. doi: 10.1016/j.sigpro.2006.09.008
[87] Vetterli M, Marziliano P, Blu T. Sampling signals with finite rate of innovation[J]. IEEE Transactions on Signal Processing, 2002, 50(6):1417-1428. doi: 10.1109/TSP.2002.1003065
[88] Bhandari A, Marziliano P. Sampling and reconstruction of sparse signals in fractional Fourier domain[J]. IEEE Signal Processing Letters, 2010, 17(3):221-224. doi: 10.1109/LSP.2009.2035242
[89] Liu Y L, Kou K I, Ho I T. New sampling formulae for non-bandlimited signals associated with linear canonical transform and nonlinear Fourier atoms[J]. Signal Processing, 2010, 90(3):933-945. doi: 10.1016/j.sigpro.2009.09.030
[90] Shi J, Liu X P, Sha X J, et al. Sampling and reconstruction of signals in function spaces associated with the linear canonical transform[J]. IEEE Transactions on Signal Processing, 2012, 60(11):6041-6047. doi: 10.1109/TSP.2012.2210887
[91] Liu X P, Shi J, Sha X J, et al. Sampling expansion in function spaces associated with the linear canonical transform[J]. Signal, Image and Video Processing, 2014, 8(1):143-148. doi: 10.1007/s11760-013-0507-5
[92] Shi J, Xiang W, Liu X P, et al. A sampling theorem for the fractional Fourier transform without band-limiting constraints[J]. Signal Processing, 2014, 98:158-165. doi: 10.1016/j.sigpro.2013.11.026
[93] Liu X P, Shi J, Sha X J, et al. A general framework for sampling and reconstruction in function spaces associated with fractional Fourier transform[J]. Signal Processing, 2015, 107:319-326. doi: 10.1016/j.sigpro.2014.04.009
[94] Bhandari A, Zayed A I. Shift-invariant and sampling spaces associated with the fractional Fourier transform domain[J]. IEEE Transactions on Signal Processing, 2012, 60(4):1627-1637. doi: 10.1109/TSP.2011.2177260
[95] Li B Z, Tao R, Xu T Z, et al. The Poisson sum formulae associated with the fractional Fourier transform[J]. Signal Processing, 2009, 89(5):851-856. doi: 10.1016/j.sigpro.2008.10.030
[96] Tao R, Li B Z, Wang Y. Spectral analysis and reconstruction for periodic nonuniformly sampled signals in fractional Fourier domain[J]. IEEE Transactions on Signal Processing, 2007, 55(7):3541-3547. doi: 10.1109/TSP.2007.893931
[97] Tao R, Li B Z, Wang Y, et al. On sampling of band-limited signals associated with the linear canonical transform[J]. IEEE Transactions on Signal Processing, 2008, 56(11):5454-5464. doi: 10.1109/TSP.2008.929333
[98] Xu L Y, Zhang F, Tao R. Fractional spectral analysis of randomly sampled signals and applications[J]. IEEE Transactions on Instrumentation and Measurement, 2017, 66(11):2869- 2881. doi: 10.1109/TIM.2017.2728438
[99] Xu L Y, Zhang F, Tao R. Randomized nonuniform sampling and reconstruction in fractional Fourier domain[J]. Signal Processing, 2016, 120:311-322. doi: 10.1016/j.sigpro.2015.09.016
[100] Liu X P, Shi J, Xiang W, et al. Sampling expansion for irregularly sampled signals in fractional Fourier transform domain[J]. Digital Signal Processing, 2014, 34:74-81. doi: 10.1016/j.dsp.2014.08.004
[101] Maymon S, Oppenheim A V. Sinc interpolation of nonuniform samples[J]. IEEE Transactions on Signal Processing, 2011, 59(10):4745-4758. doi: 10.1109/TSP.2011.2160054
[102] Zhao H, Ran Q W, Tan L Y, et al. Reconstruction of bandlimited signals in linear canonical transform domain from finite nonuniformly spaced samples[J]. IEEE Signal Processing Letters, 2009, 16(12):1047-1050. doi: 10.1109/LSP.2009.2030098
[103] Zhao H, Ran Q W, Ma J, et al. On bandlimited signals associated with linear canonical transform[J]. IEEE Signal Processing Letters, 2009, 16(5):343-345. doi: 10.1109/LSP.2009.2014290
[104] Ran Q W, Zhao H, Tan L Y, et al. Sampling of bandlimited signals in fractional Fourier transform domain[J]. Circuits, Systems and Signal Processing, 2010, 29(3):459-467. doi: 10.1007/s00034-010-9155-y
[105] Zhang F, Tao R, Wang Y. Multi-channel sampling theorems for band-limited signals with fractional Fourier transform[J]. Science in China Series E:Technological Sciences, 2008, 51(6):790-802. doi: 10.1007/s11431-008-0087-8
[106] Wei D Y, Ran Q W, Li Y M. Generalized sampling expansion for bandlimited signals associated with the fractional Fourier transform[J]. IEEE Signal Processing Letters, 2010, 17(6):595-598. doi: 10.1109/LSP.2010.2048642
[107] Shi J, Chi Y G, Zhang N T. Multichannel sampling and reconstruction of bandlimited signals in fractional Fourier domain[J]. IEEE Signal Processing Letters, 2010, 17(11):909-912. doi: 10.1109/LSP.2010.2071383
[108] Wei D Y, Ran Q W, Li Y M. Multichannel sampling and reconstruction of bandlimited signals in the linear canonical transform domain[J]. IET Signal Processing, 2011, 5(8):717-727. doi: 10.1049/iet-spr.2010.0298
[109] Wei D Y, Ran Q W, Li Y M. Reconstruction of band-limited signals from multichannel and periodic nonuniform samples in the linear canonical transform domain[J]. Optics Communications, 2011, 284(19):4307-4315. doi: 10.1016/j.optcom.2011.05.010
[110] Wei D Y, Li Y M. Multichannel sampling theorem for bandpass signals in the linear canonical transform domain[J]. Optik-International Journal for Light and Electron Optics, 2014, 125(14):3434-3438. doi: 10.1016/j.ijleo.2014.01.040
[111] Wei D Y. Multi-channel sampling expansion for band-pass signals without channels constraints[J]. Optik-International Journal for Light and Electron Optics, 2016, 127(8):4047-4052. doi: 10.1016/j.ijleo.2016.01.113
[112] Wei D Y, Li Y M. Generalized sampling expansions with multiple sampling rates for lowpass and bandpass signals in the fractional Fourier transform domain[J]. IEEE Transactions on Signal Processing, 2016, 64(18):4861-4874. doi: 10.1109/TSP.2016.2560148
[113] Shi J, Liu X P, He L, et al. Sampling and reconstruction in arbitrary measurement and approximation spaces associated with linear canonical transform[J]. IEEE Transactions on Signal Processing, 2016, 64(24):6379-6391. doi: 10.1109/TSP.2016.2602808
[114] Xu L Y, Tao R, Zhang F. Multichannel consistent sampling and reconstruction associated with linear canonical transform[J]. IEEE Signal Processing Letters, 2017, 24(5):658-662. doi: 10.1109/LSP.2017.2683535
[115] Tao R, Zhang F, Wang Y. Fractional power spectrum[J]. IEEE Transactions on Signal Processing, 2008, 56(9):4199-4206. doi: 10.1109/TSP.2008.925579
[116] Tao R, Zhang F, Wang Y. Sampling random signals in a fractional Fourier domain[J]. Signal Processing, 2011, 91(6):1394-1400. doi: 10.1016/j.sigpro.2010.11.006
[117] Torres R, Lizarazo Z, Torres E. Fractional sampling theorem for α-bandlimited random signals and its relation to the von Neumann ergodic theorem[J]. IEEE Transactions on Signal Processing, 2014, 62(14):3695-3705. doi: 10.1109/TSP.2014.2328977
[118] Huo H Y, Sun W C. Sampling theorems and error estimates for random signals in the linear canonical transform domain[J]. Signal Processing, 2015, 111:31-38. doi: 10.1016/j.sigpro.2014.11.021
[119] Almeida L B. Product and convolution theorems for the fractional Fourier transform[J]. IEEE Signal Processing Letters, 1997, 4(1):15-17. doi: 10.1109/97.551689
[120] Zayed A I. A convolution and product theorem for the fractional Fourier transform[J]. IEEE Signal Processing Letters, 1998, 5(4):101-103. doi: 10.1109/97.664179
[121] Akay O, Boudreaux-Bartels G F. Fractional convolution and correlation via operator methods and an application to detection of linear FM signals[J]. IEEE Transactions on Signal Processing, 2001, 49(5):979-993. doi: 10.1109/78.917802
[122] Zhang Z C. New convolution structure for the linear canonical transform and its application in filter design[J]. Optik-International Journal for Light and Electron Optics, 2016, 127(13):5259-5263. doi: 10.1016/j.ijleo.2016.03.025
[123] Bahri M, Amir A K, Ashino R. Correlation formulation using relationship between convolution and correlation in linear canonical transform domain[C]//Proceedings of 2017 International Conference on Wavelet Analysis and Pattern Recognition, 2017: 177-182.
https://core.ac.uk/download/pdf/141541615.pdf [124] Shi J, Liu X P, Zhang N T. Generalized convolution and product theorems associated with linear canonical transform[J]. Signal, Image and Video Processing, 2014, 8(5):967-974. doi: 10.1007/s11760-012-0348-7
[125] Shi J, Sha X J, Song X C, et al. Generalized convolution theorem associated with fractional Fourier transform[J]. Wireless Communications and Mobile Computing, 2014, 14(13):1340-1351. doi: 10.1002/wcm.v14.13
[126] Wei D Y, Ran Q W. Multiplicative filtering in the fractional Fourier domain[J]. Signal, Image and Video Processing, 2013, 7(3):575-580. doi: 10.1007/s11760-011-0261-5
[127] Goel N, Singh K, Saxena R, et al. Multiplicative filtering in the linear canonical transform domain[J]. IET Signal Processing, 2016, 10(2):173-181. doi: 10.1049/iet-spr.2015.0035
[128] Mendlovic D, Ozaktas H M, Lohmann A W. Fractional correlation[J]. Applied Optics, 1995, 34(2):303-309. doi: 10.1364/AO.34.000303
[129] Bitran Y, Zalevsky Z, Mendlovic D, et al. Fractional correlation operation:performance analysis[J]. Applied Optics, 1996, 35(2):297-303. doi: 10.1364/AO.35.000297
[130] Granieri S, Arizaga R, Sicre E E. Optical correlation based on the fractional Fourier transform[J]. Applied Optics, 1997, 36(26):6636-6645. doi: 10.1364/AO.36.006636
[131] Capus C, Brown K. Short-time fractional Fourier methods for the time-frequency representation of chirp signals[J]. The Journal of the Acoustical Society of America, 2003, 113(6):3253-3263. doi: 10.1121/1.1570434
[132] Catherall A T, Williams D P. Detecting non-stationary signals using fractional Fourier methods[EB/OL]. http://www.ima.org.uk/Conferences/mathssignalprocessing2006/williams.pdf
[133] Zhang F, Bi G A, Chen Y Q. Chip signal analysis by using adaptive short-time fractional Fourier transform[C]//Proceedings of the 2000 10th European Signal Processing Conference, 2000: 1-4.
https://www.researchgate.net/publication/282255280_Chip_signal_analysis_by_using_adaptive_short-time_fractional_Fourier_transform [134] Tao R, Li Y L, Wang Y. Short-time fractional Fourier transform and its applications[J]. IEEE Transactions on Signal Processing, 2010, 58(5):2568-2580. doi: 10.1109/TSP.2009.2028095
[135] Liu S H, Shan T, Tao R, et al. Sparse discrete fractional Fourier transform and its applications[J]. IEEE Transactions on Signal Processing, 2014, 62(24):6582-6595. doi: 10.1109/TSP.2014.2366719
[136] Hassanieh H, Indyk P, Katabi D, et al. Simple and practical algorithm for sparse Fourier transform[C]//Proceedings of the 23rd Annual ACM-SIAM Symposium on Discrete Algorithms, 2012: 1183-1194.
http://www.mit.edu/~ecprice/papers/sparse-fft-soda.pdf [137] Gilbert A C, Indyk P, Iwen M, et al. Recent developments in the sparse Fourier transform:a compressed Fourier transform for big data[J]. IEEE Signal Processing Magazine, 2014, 31(5):91-100. doi: 10.1109/MSP.2014.2329131
[138] 刘升恒. 稀疏分数傅里叶变换理论及其在探测中的应用[D]. 北京: 北京理工大学, 2016.
Liu S H. Sparse fractional Fourier transform and its applications in exploration[D]. Beijing: Beijing Institute of Technology, 2016.
http://cdmd.cnki.com.cn/Article/CDMD-10007-1018811862.htm [139] Kutay A, Ozaktas H M, Ankan O, et al. Optimal filtering in fractional Fourier domains[J]. IEEE Transactions on Signal Processing, 1997, 45(5):1129-1143. doi: 10.1109/78.575688
[140] Sharma K K, Joshi S D. Signal separation using linear canonical and fractional Fourier transforms[J]. Optics Communications, 2006, 265(2):454-460. doi: 10.1016/j.optcom.2006.03.062
[141] Barshan B, Kutay M A, Ozaktas H M. Optimal filtering with linear canonical transformations[J]. Optics Communications, 1997, 135(1-3):32-36. doi: 10.1016/S0030-4018(96)00598-6
[142] Kutay M A, Ozaktas H M. Optimal image restoration with the fractional Fourier transform[J]. Journal of the Optical Society of America A, 1998, 15(4):825-833. doi: 10.1364/JOSAA.15.000825
[143] Kutay M A. Generalized filtering configurations with applications in digital and optical signal and image processing[D]. Turkish: Bilkent University, 1999.
http://cn.bing.com/academic/profile?id=e34e4b249974b9405a1dc92e5c2784e0&encoded=0&v=paper_preview&mkt=zh-cn [144] Erden M F, Kutay M A, Ozaktas H M. Repeated filtering in consecutive fractional Fourier domains and its application to signal restoration[J]. IEEE Transactions on Signal Processing, 1999, 47(5):1458-1462. doi: 10.1109/78.757244
[145] 齐林, 陶然, 周思永, 等. LFM信号的一种最优滤波算法[J].电子学报, 2004, 32(9):1464-1467. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dianzixb200409014
Qi L, Tao R, Zhou S Y, et al. An approach for optimal filtering of LFM signal[J]. Acta Electronica Sinica, 2004, 32(9):1464-1467. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dianzixb200409014
[146] Liu F, Xu H F, Tao R, et al. Research on resolution between multi-component LFM signals in the fractional Fourier domain[J]. Science China Information Sciences, 2012, 55(6):1301-1312. doi: 10.1007/s11432-011-4324-6
[147] Tao R, Li X M, Li Y L, et al. Time-delay estimation of chirp signals in the fractional Fourier domain[J]. IEEE Transactions on Signal Processing, 2009, 57(7):2852-2855. doi: 10.1109/TSP.2009.2020028
[148] Hao H Y. Multi component LFM signal detection and parameter estimation based on EEMD-FRFT[J]. Optik-International Journal for Light and Electron Optics, 2013, 124(23):6093-6096. doi: 10.1016/j.ijleo.2013.04.104
[149] Mustard D. Uncertainty principles invariant under the fractional Fourier transform[J]. The ANZIAM Journal, 1991, 33(2):180-191. http://cn.bing.com/academic/profile?id=45c0c6baca65e59bf0ba8b95ac0cd3ba&encoded=0&v=paper_preview&mkt=zh-cn
[150] Ozaktas H M, Aytür O. Fractional Fourier domains[J]. Signal Processing, 1995, 46(1):119-124. doi: 10.1016/0165-1684(95)00076-P
[151] Aytür O, Ozaktas H M. Non-orthogonal domains in phase space of quantum optics and their relation to fractional Fourier transforms[J]. Optics Communications, 1995, 120(3-4):166-170. doi: 10.1016/0030-4018(95)00452-E
[152] Akay O, Boudreaux-Bartels G F. New fractional operators and their properties: a generalization of time and frequency operators[C]//Proceedings of 1997 UK Symposium on Applications of Time-Frequency and Time-Scale Methods, 1997: 141-144.
https://www.researchgate.net/publication/280316920_New_Fractional_Operators_and_Their_Properties_A_Generalization_of_Time_and_frequency_Operators [153] Shinde S, Gadre V M. An uncertainty principle for real signals in the fractional Fourier transform domain[J]. IEEE Transactions on Signal Processing, 2001, 49(11):2545-2548. doi: 10.1109/78.960402
[154] Capus C, Brown K. Fractional Fourier transform of the Gaussian and fractional domain signal support[J]. IEE Proceedings-Vision, Image, and Signal Processing, 2003, 150(2):99-106. doi: 10.1049/ip-vis:20030313
[155] Xu G L, Wang X T, Xu X G. Generalized entropic uncertainty principle on fractional Fourier transform[J]. Signal Processing, 2009, 89(12):2692-2697. doi: 10.1016/j.sigpro.2009.05.014
[156] Zhao J, Tao R, Li Y L, et al. Uncertainty principles for linear canonical transform[J]. IEEE Transactions on Signal Processing, 2009, 57(7):2856-2858. doi: 10.1109/TSP.2009.2020039
[157] Shi J, Liu X P, Zhang N T. On uncertainty principle for signal concentrations with fractional Fourier transform[J]. Signal Processing, 2012, 92(12):2830-2836. doi: 10.1016/j.sigpro.2012.04.008
[158] Dang P, Deng G T, Qian T. A tighter uncertainty principle for linear canonical transform in terms of phase derivative[J]. IEEE Transactions on Signal Processing, 2013, 61(21):5153-5164. doi: 10.1109/TSP.2013.2273440
[159] Mendlovic D, Lohmann A W. Space-bandwidth product adaptation and its application to superresolution:fundamentals[J]. Journal of the Optical Society of America A, 1997, 14(3):558-562. doi: 10.1364/JOSAA.14.000558
[160] 孟祥意. 分数阶傅里叶域多抽样率滤波器组理论及应用[D]. 北京: 北京理工大学, 2010.
Meng X Y. Theories and applications of multirate filter banks in fractional Fourier domain[D]. Beijing: Beijing Institute of Technology, 2010.
[161] Martone M. A multicarrier system based on the fractional Fourier transform for time-frequency-selective channels[J]. IEEE Transactions on Communications, 2001, 49(6):1011-1020. doi: 10.1109/26.930631
[162] Tao R, Meng X Y, Wang Y. Transform order division multiplexing[J]. IEEE Transactions on Signal Processing, 2011, 59(2):598-609. doi: 10.1109/TSP.2010.2089680
[163] Tao R, Xin Y, Wang Y. Double image encryption based on random phase encoding in the fractional Fourier domain[J]. Optics Express, 2007, 15(24):16067-16079. doi: 10.1364/OE.15.016067
[164] Tao R, Meng X Y, Wang Y. Image encryption with multiorders of fractional Fourier transforms[J]. IEEE Transactions on Information Forensics and Security, 2010, 5(4):734-738. doi: 10.1109/TIFS.2010.2068289
[165] Sun H B, Liu G S, Gu H, et al. Application of the fractional Fourier transform to moving target detection in airborne SAR[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(4):1416-1424. doi: 10.1109/TAES.2002.1145767
[166] Tao R, Zhang N, Wang Y. Analysing and compensating the effects of range and Doppler frequency migrations in linear frequency modulation pulse compression radar[J]. IET Radar, Sonar & Navigation, 2011, 5(1):12-22. http://cn.bing.com/academic/profile?id=00813bb870b49fe328c1acf116a37b19&encoded=0&v=paper_preview&mkt=zh-cn
[167] Pang C S, Shan T, Tao R, et al. Detection of high-speed and accelerated target based on the linear frequency modulation radar[J]. IET Radar, Sonar & Navigation, 2014, 8(1):37-47. http://cn.bing.com/academic/profile?id=4bcef927b048043214603b31820544b1&encoded=0&v=paper_preview&mkt=zh-cn
[168] Guan J, Chen X L, Huang Y, et al. Adaptive fractional Fourier transform-based detection algorithm for moving target in heavy sea clutter[J]. IET Radar, Sonar & Navigation, 2012, 6(5):389-401. http://cn.bing.com/academic/profile?id=b7a876992e0603f7275c73b94657b98f&encoded=0&v=paper_preview&mkt=zh-cn
[169] 陈喆, 王宏禹, 邱天爽.基于分数阶傅立叶变换的模糊函数的研究[J].信号处理, 2003, 19(6):499-502. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xhcl200306001
Chen Z, Wang H Y, Qiu T S. The study of ambiguity function based on fractional Fourier transform[J]. Signal Processing, 2003, 19(6):499-502. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xhcl200306001
[170] Chen X L, Guan J, Bao Z H, et al. Detection and extraction of target with micromotion in spiky sea clutter via short-time fractional Fourier transform[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(2):1002-1018. doi: 10.1109/TGRS.2013.2246574
[171] Chen X L, Guan J, Liu N B, et al. Maneuvering target detection via Radon-fractional Fourier transform-based long-time coherent integration[J]. IEEE Transactions on Signal Processing, 2014, 62(4):939-953. doi: 10.1109/TSP.2013.2297682
[172] Tian J, Xia X G, Cui W, et al. A coherent integration method via Radon-NUFrFT for random PRI radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(4):2010-2109. http://cn.bing.com/academic/profile?id=8e5555c987eccb757cf17b97708817f9&encoded=0&v=paper_preview&mkt=zh-cn
[173] Amein A S, Soraghan J J. A new chirp scaling algorithm based on the fractional Fourier transform[J]. IEEE Signal Processing Letters, 2005, 12(10):705-708. doi: 10.1109/LSP.2005.855547
[174] Yi H, Fan C Y, Yang J G, et al. Imaging and locating multiple ground moving targets based on keystone transform and FrFT for single channel SAR system[C]//Proceedings of the 2nd Asian-Pacific Conference on Synthetic Aperture Radar, 2009: 771-774.
https://ieeexplore.ieee.org/document/5374170/ [175] Wang W Q. Moving target indication via three-antenna SAR with simplified fractional Fourier transform[J]. EURASIP Journal on Advances in Signal Processing, 2011, 2011(1):117. doi: 10.1186/1687-6180-2011-117
[176] Wang Q, Pepin M, Beach R J, et al. SAR-based vibration estimation using the discrete fractional Fourier transform[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(10):4145-4156. doi: 10.1109/TGRS.2012.2187665
[177] Bu H X, Bai X, Tao R. Compressed sensing SAR imaging based on sparse representation in fractional Fourier domain[J]. Science China Information Sciences, 2012, 55(8):1789-1800. doi: 10.1007/s11432-012-4607-6
[178] Sun G C, Xing M D, Xia X G, et al. A unified focusing algorithm for several modes of SAR based on FrFT[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(5):3139-3155. doi: 10.1109/TGRS.2012.2212280
[179] Singh J, Datcu M. SAR image categorization with log cumulants of the fractional Fourier transform coefficients[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(12):5273-5282. doi: 10.1109/TGRS.2012.2230892
[180] Chen S, Zhang S N, Zhao H C, et al. A new chirp scaling algorithm for highly squinted missile-borne SAR based on FrFT[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(8):3977-3987. doi: 10.1109/JSTARS.2014.2360192
[181] Pelich R, Longépé N, Mercier G, et al. Vessel refocusing and velocity estimation on SAR imagery using the fractional Fourier transform[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(3):1670-1684. doi: 10.1109/TGRS.2015.2487378
[182] 王腾. Chirp基物理层安全通信信号设计及处理技术[D]. 北京: 北京理工大学, 2017.
Wang T. Chirp-based physical-layer secure communication signal design and processing[D]. Beijing: Beijing Institute of Technology, 2017.
[183] 陈恩庆, 陶然, 张卫强.一种基于分数阶傅立叶变换的时变信道参数估计方法[J].电子学报, 2005, 33(12):2101-2104. doi: 10.3321/j.issn:0372-2112.2005.12.002
Chen E Q, Tao R, Zhang W Q. A method for time-varying channel parameter estimation based on fractional Fourier transform[J]. Acta Electronica Sinica, 2005, 33(12):2101-2104. doi: 10.3321/j.issn:0372-2112.2005.12.002
[184] 陈恩庆, 陶然, 张卫强, 等.一种基于分数阶傅里叶变换的OFDM系统及其均衡算法[J].电子学报, 2007, 35(3):409-414. https://www.wenkuxiazai.com/doc/985dd96a561252d380eb6eb1.html
Chen E Q, Tao R, Zhang W Q, et al. The OFDM system and equalization algorithm based on the fractional Fourier transform[J]. Acta Electronica Sinica, 2007, 35(3):409-414. https://www.wenkuxiazai.com/doc/985dd96a561252d380eb6eb1.html
[185] Yang Q, Tao R, Wang Y, et al. MIMO-OFDM system based on fractional Fourier transform and selecting algorithm for optimal order[J]. Science in China Series F: Information Sciences, 2008, 51(9):1360-1371. doi: 10.1007/s11432-008-0123-0
[186] Zheng J, Wang Z L. ICI analysis for FRFT-OFDM systems to frequency offset in time-frequency selective fading channels[J]. IEEE Communications Letters, 2010, 14(10):888-890. doi: 10.1109/LCOMM.2010.072910.100562
[187] Wang H Q, Ma H. MIMO OFDM systems based on the optimal fractional Fourier transform[J]. Wireless Personal Communications, 2010, 55(2):265-272. doi: 10.1007/s11277-009-9800-6
[188] Wang H Q. A novel multiuser SISO-BOFDM systems with group fractional Fourier transforms scheme[J]. Wireless Personal Communications, 2013, 69(2):735-743. doi: 10.1007/s11277-012-0609-3
[189] Kumari S, Rai S K, Kumar A, et al. Exact BER analysis of FRFT-OFDM system over frequency selective Rayleigh fading channel with CFO[J]. Electronics Letters, 2013, 49(20):1299-1301. doi: 10.1049/el.2013.0980
[190] Mokhtari Z, Sabbaghian M. Near-optimal angle of transform in FRFT-OFDM systems based on ICI analysis[J]. IEEE Transactions on Vehicular Technology, 2016, 65(7):5777-5783. doi: 10.1109/TVT.2015.2460331
[191] Cheng M, Deng L, Wang X, et al. Enhanced secure strategy for OFDM-PON system by using hyperchaotic system and fractional Fourier transformation[J]. IEEE Photonics Journal, 2014, 6(6):7903409. https://www.researchgate.net/profile/Mengfan_Cheng/publication/271428797_Enhanced_Secure_Strategy_for_OFDM-PON_System_by_Using_Hyperchaotic_System_and_Fractional_Fourier_Transformation/links/54c765380cf289f0cecd0d88.pdf?inViewer=true&disableCoverPage=true&origin=publication_detail
[192] Deng L, Cheng M F, Wang X L, et al. Secure OFDM-PON system based on chaos and fractional Fourier transform techniques[J]. Journal of Lightwave Technology, 2014, 32(15):2629-2635. doi: 10.1109/JLT.2014.2331066
[193] Wen H, Tang J, Wu J S, et al. A cross-layer secure communication model based on Discrete Fractional Fourier Fransform (DFRFT)[J]. IEEE Transactions on Emerging Topics in Computing, 2015, 3(1):119-126. doi: 10.1109/TETC.2014.2367415
[194] Wang T, Huan H, Tao R, et al. Security-coded OFDM system based on multiorder fractional Fourier transform[J]. IEEE Communications Letters, 2016, 20(12):2474-2477. doi: 10.1109/LCOMM.2016.2611498
[195] Wang T, Huan H, Tao R, et al. Anti-eavesdropping FrFT-OFDM System exploiting multipath channel characteristics[J]. IET Communications, 2017, 11(9):1371-1378. doi: 10.1049/iet-com.2016.1251
[196] Chen L F, Zhao D M, Ge F. Image encryption based on singular value decomposition and Arnold transform in fractional domain[J]. Optics Communications, 2013, 291:98-103. doi: 10.1016/j.optcom.2012.10.080
[197] Keshari S, Modani S G. Color image encryption scheme based on 4-weighted fractional Fourier transform[J]. Journal of Electronic Imaging, 2012, 21(3):033018. http://cn.bing.com/academic/profile?id=2729fc37e545d26f4a86cbf06e495a56&encoded=0&v=paper_preview&mkt=zh-cn
[198] Joshi M, Chandrashakher, Singh K. Color image encryption and decryption for twin images in fractional Fourier domain[J]. Optics Communications, 2008, 281(23):5713-5720. doi: 10.1016/j.optcom.2008.08.024
[199] Unnikrishnan G, Joseph J, Singh K. Optical encryption by double-random phase encoding in the fractional Fourier domain[J]. Optics Letters, 2000, 25(12):887-889. doi: 10.1364/OL.25.000887
[200] Liu S T, Yu L, Zhu B H. Optical image encryption by cascaded fractional Fourier transforms with random phase filtering[J]. Optics Communications, 2001, 187(1-3):57-63. doi: 10.1016/S0030-4018(00)01093-2
[201] Hennelly B, Sheridan J T. Optical image encryption by random shifting in fractional Fourier domains[J]. Optics Letters, 2003, 28(4):269-271. doi: 10.1364/OL.28.000269
[202] Liu Z J, Liu S T. Double image encryption based on iterative fractional Fourier transform[J]. Optics Communications, 2007, 275(2):324-329. doi: 10.1016/j.optcom.2007.03.039
[203] Joshi M, Shakher C, Singh K. Logarithms-based RGB image encryption in the fractional Fourier domain:a non-linear approach[J]. Optics and Lasers in Engineering, 2009, 47(6):721-727. doi: 10.1016/j.optlaseng.2008.11.003
[204] Singh N, Sinha A. Optical image encryption using improper Hartley transforms and chaos[J]. Optik-International Journal for Light and Electron Optics, 2010, 121(10):918-925. doi: 10.1016/j.ijleo.2008.09.049
[205] Sui L S, Gao B. Single-channel color image encryption based on iterative fractional Fourier transform and chaos[J]. Optics & Laser Technology, 2013, 48:117-127. http://cn.bing.com/academic/profile?id=98b98883c0e184501696ae2ef84bbc67&encoded=0&v=paper_preview&mkt=zh-cn
[206] Lu M F, Zhang F, Tao R, et al. Parameter estimation of optical fringes with quadratic phase using the fractional Fourier transform[J]. Optics and Lasers in Engineering, 2015, 74:1-16. http://cn.bing.com/academic/profile?id=6201a24d4bb73cd48317dbe78d902951&encoded=0&v=paper_preview&mkt=zh-cn
[207] Nascov V, Dobroiu A, Apostol D, et al. Statistical errors on Newton fringe pattern digital processing[J]. Proceedings of SPIE, 2004, 5581:788-796. http://cn.bing.com/academic/profile?id=99e45c050ac3c5778b92fbeae9ab16b4&encoded=0&v=paper_preview&mkt=zh-cn
[208] Nascov V, Apostol D, Garoi F. Statistical processing of Newton's rings using discrete Fourier analysis[J]. Optical Engineering, 2007, 46(2):028201. doi: 10.1117/1.2709856
[209] Gorthi S S, Rastogi P. Estimation of phase derivatives using discrete chirp-Fourier-transform-based method[J]. Optics Letters, 2009, 34(16):2396-2398. doi: 10.1364/OL.34.002396
[210] Wu J M, Lu M F, Tao R, et al. Improved FRFT-based method for estimating the physical parameters from Newton's rings[J]. Optics and Lasers in Engineering, 2017, 91:178-186. doi: 10.1016/j.optlaseng.2016.11.021
[211] Guo Y, Li B Z. Novel method for parameter estimation of Newton's rings based on CFRFT and ER-WCA[J]. Signal Processing, 2018, 144:118-126. doi: 10.1016/j.sigpro.2017.10.005
[212] Parot V, Sing-Long C, Lizama C, et al. Application of the fractional Fourier transform to image reconstruction in MRI[J]. Magnetic Resonance in Medicine, 2012, 68(1):17-29. doi: 10.1002/mrm.23190
[213] 尚宇, 徐婷, 何永辉.分数阶傅里叶变换在心电信号处理中的应用[J].电子科技, 2011, 24(8):116-118. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZEDI201008001098.htm
Shang Y, Xu T, He Y H. The applications of the fractional Fourier transform in the ECG processing[J]. Electronic Science and Technology, 2011, 24(8):116-118. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZEDI201008001098.htm
[214] Jing X Y, Wong H S, Zhang D. Face recognition based on discriminant fractional Fourier feature extraction[J]. Pattern Recognition Letters, 2006, 27(13):1465-1471. doi: 10.1016/j.patrec.2006.02.020
[215] Liu Z F, Lu X Y. Face recognition based on fractional Fourier transform and PCA[C]//Proceedings of 2011 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference, 2011: 1406-1409.
https://ieeexplore.ieee.org/document/6037228/ [216] 辛怡, 白雪霏, 李勤. 分数阶傅里叶联合变换相关在指纹识别中的应用[C]//中国仪器仪表学会医疗仪器分会2010两岸四地生物医学工程学术年会论文集, 2010.
Xin Y, Bai X F, Li Q. Utilizing joint fractional Fourier transform correlator to fingerprint recognition[C]//China Instrument and Control Society, 2010.
http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGYF201009001046.htm [217] 钱晓红. 分数阶傅里叶变换在耳语音说话人识别研究中的应用[D]. 苏州: 苏州大学, 2012.
Qian X H. Fractional Fourier transform and its application in whispered speaker identification[D]. Suzhou: Soochow University, 2012.
http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2120386 [218] 宋秀, 尉宇.基于短时分数阶傅里叶变换的异步电机转子断条故障诊断[J].武汉科技大学学报, 2016, 39(2):145-149. http://cdmd.cnki.com.cn/Article/CDMD-10614-2006113109.htm
Song X, Wei Y. Fault diagnosis of broken rotor bar in asynchronous motor based on short-time fractional Fourier transform[J]. Journal of Wuhan University of Science and Technology, 2016, 39(2):145-149. http://cdmd.cnki.com.cn/Article/CDMD-10614-2006113109.htm
[219] 吕亚平. 基于时频分析的机械故障盲源分离方法研究[D]. 郑州: 郑州大学, 2009.
Lv Y P. Blind source separation of machine faults based on time-frequency analysis[D]. Zhengzhou: Zhengzhou University, 2009.
http://cdmd.cnki.com.cn/Article/CDMD-10459-2010052104.htm -
访问统计


 E-mail Alert
E-mail Alert RSS
RSS
 下载:
下载: