-
摘要
如何在低阈值小尺度(毫瓦或皮焦量级、微米以下)情况下激发非线性光学效应是近年来光学领域研究的重要课题。该研究最直接的应用需求就是光子集成芯片,这是未来实现超高速、大容量信息网络体系的基础。光子晶体具有类似于半导体能带的光子禁带(PBG),被誉为“光子半导体”,为人们提供了一种新颖而又实用的操纵光子的物理手段,使低阈值、可集成非线性效应产生成为可能。越来越多的非线性效应在光子晶体中已经被发现,例如光子晶体慢光、带隙孤子、电磁感应透明、二次谐波产生、光学双稳态等,本文将着重对可用于光子集成器件开发的光子晶体非线性效应研究领域的一些主要成果和进展进行总结,介绍其相关应用并对光子晶体非线性效应研究作出展望。
-
关键词:
- 光子晶体 /
- 非线性光学效应 /
- 低阈值集成光学非线性 /
- 光子集成器件
Abstract
How to excite the nonlinear optical effect in the case of low threshold (mW or pJ order) and small scale (μm or less) is a topic field of optical research in recent years. The most direct application requirement is photonic integrated circuit, which is the foundation to realize the ultra-high speed and large capacity information network in the future. Photonic crystals (PCs) have the photonic band gap (PBG) just like the semiconductor band for electronics, so it is known as "photonic semiconductors". PCs provide a novel and practical means of manipulating photons, therefore the possibility of photonic integrated circuit with low threshold arises. More and more nonlinear effects have been found in PCs, such as photonic crystal slow light, the band gap soliton, electromagnetic induction transparency, second harmonic generation and optical bistability. This paper will focus on the summaries of some major achievements and advances about PCs that would promote the nonlinear photonic integrated devices. Certainly the related applications will be introduced and the future outlook of the nonlinear PCs will be discussed.
-
Overview

Abstract:Photonic integrated circuit (or chip) is the foundation of the ultra-high speed and large capacity information network in the future. This leads to a hot point of optical research in recent years that is how to excite the nonlinear optical effect in the case of low threshold (mW or pJ order) and small scale (μm or less). As is known to all, the nonlinear optical effect is too weak to be excited under normal conditions. That is why the nonlinear optics failed to develop before the appearance of laser. In other words, how to excite the nonlinear optical effect in the case of low threshold and small scale is difficult. In recent years, researchers found that the nonlinear optical effect could be greatly enhanced in the photonic crystals (PCs) which are expected to solve this problem.
PC is a artificial periodic nanostructure composed of periodic dielectric. The most typical feature of PC is photonic band gap (PBG). Photons either propagate through this structure or not, depending on their wavelengths in or out of the PBG. The motion of photons in PCs is much the same way as that ionic lattices affect electrons in solids. So PC is also known as “semiconductor crystal for photons”. Thanks to the PBG, the nonlinear optical effects in PCs are more abundant and outstanding. For instance, the nanocavity based on the PCs can get the extremely high Q-factor leading to the low threshold and efficient nonlinear optical effect. Again, at the edge of PBG, the electromagnetic field is violently modulated leading to the huge electric field gradient that creates the conditions for high-order nonlinear effect. Additionally, the periodic optical nanostructure of PCs provides the favorable term for nonlinear enhancement,such as the quasi phase matching that is necessary for second harmonic generation. Moreover, the electromagnetic field resonance and coupling among the discrete components of PCs, nano-waveguide and nano-cavity etc. can be used as the powerful methods to custom-tailor the nonlinear optical effect.
More and more nonlinear effects have been found in PCs, such as photonic crystal slow light, the band gap soliton, electromagnetic induction transparency, second harmonic generation, and optical bistability. This paper focuses on the summaries of some major achievements and advances about PCs that would promote the nonlinear photonic integrated devices. Certainly, the related applications are introduced and the future outlook of the nonlinear PCs is discussed.
-

-
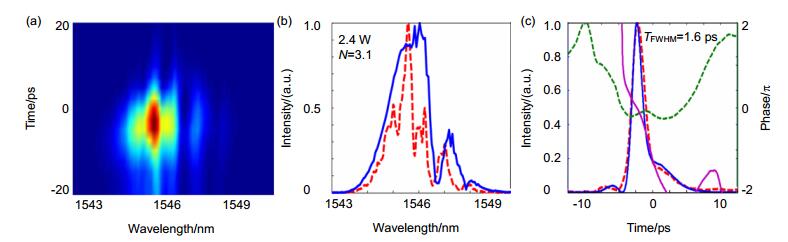
图 7 时间分辨孤子压缩测量[40]. (a)实验FREG谱. (b)测量(红色虚线)和理论(蓝色实线)的脉冲强度强度. (c)时域脉冲强度和位相(红色和绿色虚线为测量强度和位相,蓝色和棕色实线为理论强度和位相).
Figure 7. Time-resolved measurements of soliton compression [40]. (a) Experimental FREG spectrograms. (b) Measured (dashed red) and modelled (blue) intensity in the spectral domain. (c) Measured intensity (dashed red) and phase (dashed green) along with the numerical intensity (blue) and phase (magenta) in the time domain.
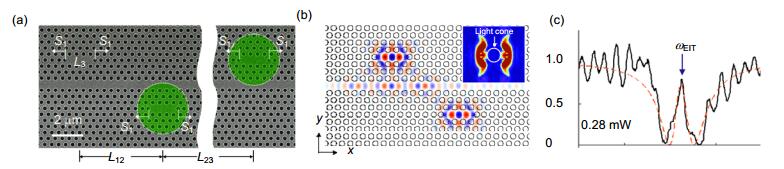
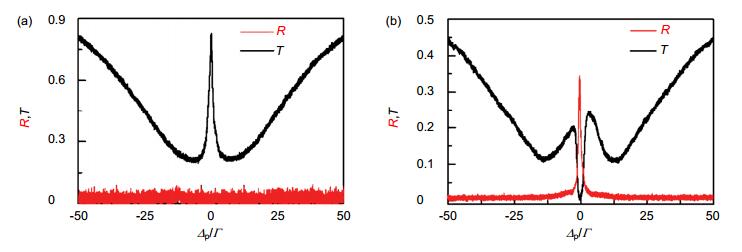
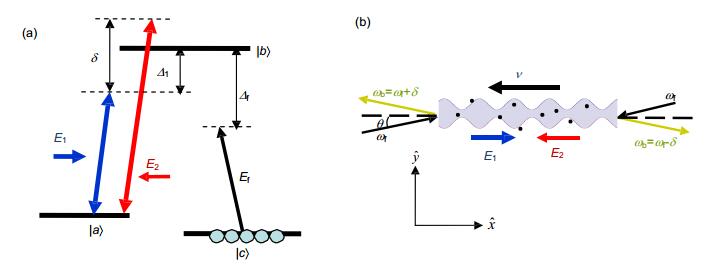
图 11 EIT光子晶体实验结果(红色线为反射光,黑色线为透射光) [49]. (a)无驻波场信号光透射. (b)有驻波时信号光被反射.
Figure 11. Experimental result of EIT photonic crystals (red curve for reflection and black curve for transmission) [49]. (a) Probe field is transmitted when the backward coupling field is absent. (b) Probe field is reflected when the system is coupled by standing wave.
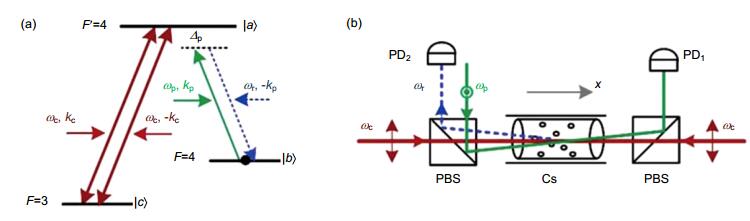
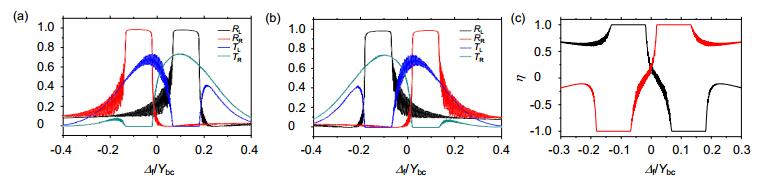
图 13 不同失谐量时光二极管实验结果[50]. (a) δ=0.2Υbc. (b) δ= -0.2Υbc. (c)对应(a)(黑色)、(b)(红色)的传输对比度. Υbc为能级|b〉和|c〉间的退相干度.
Figure 13. Experimental results of photonic diode with different detuning δ [50]. (a) δ=0.2Υbc. (b) δ= - 0.2Υbc. (c) Contrast of the transmittance for (a) (black) and (b) (red). Υbc: decoherence rate between levels |b〉 and |c〉.
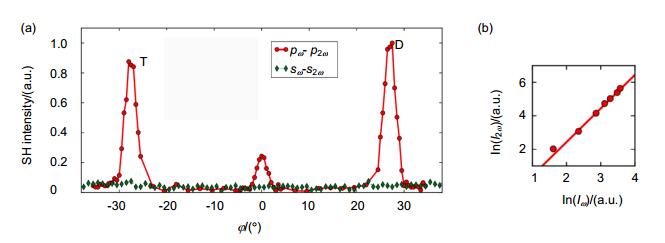
图 14 一维光子晶体Laue衍射SHG方案示意图[59]. (a)光子晶体结构和入射光位置示意图. (b)基频光和倍频光Bormann和反Bormann模式波矢位相匹配示意图.
Figure 14. Schematic view of SHG in 1D PCs in the Laue geometry [59]. (a) Schematic diagram of PCs and incident light. (b) Quasi phase matching sketch by Borrmann and anti-Borrmann eigenvectors of the PCs for the fundamental (red) and SH (blue) waves.
-
参考文献
[1] Joannopoulos J D, Villeneuve P R, Fan Shanhui. Photonic crystals: putting a new twist on light[J]. Nature, 1997, 386(6621): 143-149. doi: 10.1038/386143a0
[2] Benisty H, Weisbuch C, Labilloy D, et al. Optical and confinement properties of two-dimensional photonic crystals[J]. Journal of Lightwave Technology, 1999, 17(11): 2063-2077. doi: 10.1109/50.802996
[3] Srinivasan K, Barclay P E, Painter O, et al. Experimental demonstration of a high quality factor photonic crystal microcavity[J]. Applied Physics Letters, 2003, 83(10): 1915-1917. doi: 10.1063/1.1606866
[4] Ryu H Y, Kwon S H, Lee Y J, et al. Very-low-threshold photonic band-edge lasers from free-standing triangular photonic crystal slabs[J]. Applied Physics Letters, 2002, 80(19): 3476. doi: 10.1063/1.1477617
[5] Englund D, Shields B, Rivoire K, et al. Deterministic coupling of a single nitrogen vacancy center to a photonic crystal cavity[J]. Nano Letters, 2010, 10(10): 3922-3926. doi: 10.1021/nl101662v
[6] McGurn A R. Photonic crystal waveguide weakly interacting with multiple off-channel resonant features formed of Kerr nonlinear dielectric media[J]. Advances in OptoElectronics, 2007, 2007: 92901. https://www.researchgate.net/publication/26487081_Photonic_Crystal_Waveguide_Weakly_Interacting_with_Multiple_Off-Channel_Resonant_Features_Formed_of_Kerr_Nonlinear_Dielectric_Media
[7] Zayats A V, Smolyaninov I I, Maradudin A A. Nano-optics of surface plasmon polaritons[J]. Physics Reports, 2005, 408(3-4): 131-314. doi: 10.1016/j.physrep.2004.11.001
[8] Pitarke J M, Silkin V M, Chulkov E V, et al. Theory of surface plasmons and surface-plasmon polaritons[J]. Reports on Progress in Physics, 2007, 70: 1-87. doi: 10.1088/0034-4885/70/1/R01
[9] Russell P. Photonic crystal fibers[M]. Beijing: Peking University Press, 2013.
[10] Hansen K P. Introduction to nonlinear photonic crystal fibers[J]. Journal of Optical and Fiber Communications Reports, 2005, 2(3): 226-254. doi: 10.1007/s10297-004-0021-1
[11] Knight J C, Skryabin D V. Nonlinear waveguide optics and photonic crystal fibers[J]. Optics Express, 2007, 15(23): 15365-15376. doi: 10.1364/OE.15.015365
[12] Mori D, Baba T. Wideband and low dispersion slow light by chirped photonic crystal coupled waveguide[J]. Optics Express, 2005, 13(23): 9398-9408. doi: 10.1364/OPEX.13.009398
[13] Schulz S A, O'Faolain L, Beggs D M, et al. Dispersion engineered slow light in photonic crystals: a comparison[J]. Journal of Optics, 2010, 12(10): 104004. doi: 10.1088/2040-8978/12/10/104004
[14] 沈宏君, 田慧平, 纪越峰.一种新型无色散慢光光子晶体薄板波导[J].物理学报, 2010, 59(4): 2820-2826. doi: 10.7498/aps.59.2820
Shen Hongjun, Tian Huiping, Ji Yuefeng. A novel photonic crystal slab waveguide with dispersionless slow light[J]. Acta Physica Sinica, 2010, 59(4): 2820-2826. doi: 10.7498/aps.59.2820
[15] Li Juntao, White T P, O'Faolain L, et al. Systematic design of flat band slow light in photonic crystal waveguides[J]. Optics Express, 2008, 16(9): 6227-6232. doi: 10.1364/OE.16.006227
[16] Frandsen L H, Lavrinenko A V, Fage-Pedersen J, et al. Photonic crystal waveguides with semi-slow light and tailored dispersion properties[J]. Optics Express, 2006, 14(20): 9444-9450. doi: 10.1364/OE.14.009444
[17] Baba T. Slow light in photonic crystals[J]. Nature Photonics, 2008, 2(8): 465-473. doi: 10.1038/nphoton.2008.146
[18] Pourmand M, Karimkhani A, Moravvej-Farshi M K. Slow light photonic crystal waveguides with large delay-bandwidth product[J]. Optical Engineering, 2016, 55(12): 123108. doi: 10.1117/1.OE.55.12.123108
[19] Wu Hong, Citrin D S, Jiang Liyong, et al. Polarization-independent slow light in annular photonic crystals[J]. Applied Physics Letters, 2013, 102(14): 141112. doi: 10.1063/1.4801977
[20] Notomi M, Kuramochi E, Tanabe T. Large-scale arrays of ultrahigh-Q coupled nanocavities[J]. Nature Photonics, 2008, 2(12): 741-747. doi: 10.1038/nphoton.2008.226
[21] 陈志刚.奇妙的空间光孤子[J].物理, 2001, 30(12): 752-756. doi: 10.3321/j.issn:0379-4148.2001.12.004
Chen Zhigang. Fascinating behavior of optical spatial solitons[J]. Physics, 2001, 30(12): 752-756. doi: 10.3321/j.issn:0379-4148.2001.12.004
[22] Chen Wei, Mills D L. Gap solitons and the nonlinear optical response of superlattices[J]. Physical Review Letters, 1987, 58(2): 160-163. doi: 10.1103/PhysRevLett.58.160
[23] Ouzounov D G, Ahmad F R, Müller D, et al. Generation of megawatt optical solitons in hollow-core photonic band-gap fibers[J]. Science, 2003, 301(5640): 1702-1704. doi: 10.1126/science.1088387
[24] Ouzounov D G, Hensley C J, Gaeta A, et al. Soliton pulse compression in photonic band-gap fibers[J]. Optics Express, 2005, 13(16): 6153-6159. doi: 10.1364/OPEX.13.006153
[25] Chiao R Y. Introduction to spatial solitons[M]. Trillo S, Torruellas W. Spatial Solitons. Berlin Heidelberg: Springer, 2001: 1-18.
[26] Duree Jr G, Shultz J L, Salamo G J, et al. Observation of self-trapping of an optical beam due to the photorefractive effect[J]. Physical Review Letters, 1993, 71(4): 533-536. doi: 10.1103/PhysRevLett.71.533
[27] Chen Zhigang, Segev M, Christodoulides D N. Optical spatial solitons: historical overview and recent advances[J]. Reports on Progress in Physics Physical Society, 2012, 75(8): 086401. doi: 10.1088/0034-4885/75/8/086401
[28] Sukhorukov A A, Kivshar Y S. Spatial optical solitons in nonlinear photonic crystals[J]. Physical Review E, 2002, 65(3): 036609. doi: 10.1103/PhysRevE.65.036609
[29] Gorza S P, Taillaert D, Baets R, et al. Experimental characterization of optical-gap solitons in a one-dimensional photonic crystal made of a corrugated semiconductor planar waveguide[J]. Physical Review B, 2006, 74(23): 235327. doi: 10.1103/PhysRevB.74.235327
[30] Xie Ping, Zhang Zhaoqing, Zhang Xiangdong. Gap solitons and soliton trains in finite-sized two-dimensional periodic and quasiperiodic photonic crystals[J]. Physical Review E, 2003, 67(2): 026607. doi: 10.1103/PhysRevE.67.026607
[31] Tian Huiping, Yang Daquan, Liu Lingyu, et al. Broadband and low-power bright soliton propagation in line-defect photonic crystal waveguide[J]. Optical Engineering, 2013, 52(5): 055006. doi: 10.1117/1.OE.52.5.055006
[32] Zeng Jianhua, Malomed B A. Two-dimensional intraband solitons in lattice potentials with local defects and self-focusing nonlinearity[J]. Journal of the Optical Society of America B, 2013, 30(7): 1786-1793. doi: 10.1364/JOSAB.30.001786
[33] Inoue K, Oda H, Ikeda N, et al. Enhanced third-order nonlinear effects in slow-light photonic-crystal slab waveguides of line-defect.[J]. Optics Express, 2009, 17(9):7206-16. doi: 10.1364/OE.17.007206
[34] Matsuda N, Kato T, Harada K. Slow light enhanced optical nonlinearity in a silicon photonic crystal coupled-resonator optical waveguide.[J]. Optics Express, 2011, 19(21): 19861. doi: 10.1364/OE.19.019861
[35] Suzuki K, Hamachi Y, Baba T. Fabrication and characterization of chalcogenide glass photonic crystal waveguides[J]. Optics Express, 2009, 17(25): 22393-22400. doi: 10.1364/OE.17.022393
[36] Monat C, Corcoran B, Ebnali-Heidari M, et al. Slow light enhancement of nonlinear effects in silicon engineered photonic crystal waveguides[J]. Optics Express, 2009, 17(4): 2944- 2953. doi: 10.1364/OE.17.002944
[37] Peccianti M, Ferrera M, Razzari L, et al. Subpicosecond optical pulse compression via an integrated nonlinear chirper[J]. Optics Express, 2010, 18(8): 7625-7633. doi: 10.1364/OE.18.007625
[38] Liao Meisong, Chaudhari C, Qin Guanshi, et al. Tellurite microstructure fibers with small hexagonal core for supercontinuum generation[J]. Optics Express, 2009, 17(14): 12174-12182. doi: 10.1364/OE.17.012174
[39] Colman P, Husko C, Combrié S, et al. Temporal solitons and pulse compression in photonic crystal waveguides[J]. Nature Photonics, 2010, 4(12): 862-868. doi: 10.1038/nphoton.2010.261
[40] Blanco-Redondo A, Husko C, Eades D, et al. Observation of soliton compression in silicon photonic crystals[J]. Nature Communications, 2014, 5: 3160. https://www.researchgate.net/profile/Chad_Husko/publication/259724438_Observation_of_soliton_compression_in_silicon_photonic_crystals/links/542374e90cf26120b7a6c787.pdf?inViewer=true&disableCoverPage=true&origin=publication_detail
[41] Eisaman M D, André A, Massou F, et al. Electromagnetically induced transparency with tunable single-photon pulses[J]. Nature, 2005, 438(7069): 837-841. doi: 10.1038/nature04327
[42] Fleischhauer M, Imamoglu A, Marangos J P. Electromagnetically induced transparency: Optics in coherent media[J]. Reviews of Modern Physics, 2005, 77(2): 633-673. doi: 10.1103/RevModPhys.77.633
[43] Boller K J, Imamoğlu A, Harris S E. Observation of electromagnetically induced transparency[J]. Physical Review Letters, 1991, 66(20): 2593-2596. doi: 10.1103/PhysRevLett.66.2593
[44] Yanik M F, Suh W, Wang Zheng, et al. Stopping light in a waveguide with an all-optical analog of electromagnetically induced transparency[J]. Physical Review Letters, 2005, 93(23): 233903. https://www.researchgate.net/publication/8129119_Stopping_Light_in_a_Waveguide_with_an_All-Optical_Analog_of_Electromagnetically_Induced_Transparency
[45] Xu Qianfan, Sandhu S, Povinelli M L, et al. Experimental realization of an on-chip all-optical analogue to electromagnetically induced transparency[J]. Physical Review Letters, 2006, 96(12): 123901. doi: 10.1103/PhysRevLett.96.123901
[46] Xiao Y F, Gao J, Zou X B, et al. Coupled quantum electrodynamics in photonic crystal cavities towards controlled phase gate operations[J]. New Journal of Physics, 2008, 10(12): 123013. doi: 10.1088/1367-2630/10/12/123013
[47] Yang Xiaodong, Yu Mingbin, Kwong D L, et al. All-optical analog to electromagnetically induced transparency in multiple coupled photonic crystal cavities[J]. Physical Review Letters, 2009, 102(17): 173902. doi: 10.1103/PhysRevLett.102.173902
[48] Kocaman S, Yang X, McMillan J F, et al. Observations of temporal group delays in slow-light multiple coupled photonic crystal cavities[J]. Applied Physics Letters, 2010, 96(22): 221111. doi: 10.1063/1.3446893
[49] Wang Dan, Wu Jinze, Zhang Junxiang. Optical control of light propagation in photonic crystal based on electromagnetically induced transparency[J]. Chinese Physics B, 2016, 25(6): 064202. doi: 10.1088/1674-1056/25/6/064202
[50] Wang Dawei, Zhou Haitao, Guo Miaojun, et al. Optical diode made from a moving photonic crystal[J]. Physical Review Letters, 2013, 110(9): 093901. doi: 10.1103/PhysRevLett.110.093901
[51] Ooi C H R, Kam C H. Controlling quantum resonances in photonic crystals and thin films with electromagnetically induced transparency[J]. Physical Review B, 2010, 81(19): 195119. doi: 10.1103/PhysRevB.81.195119
[52] Li Yongyao, Malomed B A, Feng Mingneng, et al. Arrayed and checkerboard optical waveguides controlled by the electromagnetically induced transparency[J]. Physical Review A, 2010, 82(6): 063813. doi: 10.1103/PhysRevA.82.063813
[53] Yu N E, Ro J H, Cha M, et al. Broadband quasi-phase-matched second-harmonic generation in MgO-doped periodically poled LiNbO3 at the communications band[J]. Optics Letters, 2002, 27(12): 1046-1048. doi: 10.1364/OL.27.001046
[54] Ashihara S, Shimura T, Kuroda K. Group-velocity matched second-harmonic generation in tilted quasi-phase-matched gratings[J]. Journal of the Optical Society of America B, 2003, 20(5): 853-856. doi: 10.1364/JOSAB.20.000853
[55] Arie A, Habshoosh N, Bahabad A. Quasi phase matching in two-dimensional quadratic nonlinear photonic crystals[M]. Sibilia C, Benson T M, Marciniak M, et al. Photonic Crystals: Physics and Technology. Milan: Springer, 2008: 45-60.
[56] Ren Mingliang, Ma Dongli, Li Zhiyuan. Experimental demonstration of super quasi-phase matching in nonlinear photonic crystal[J]. Optics Letters, 2011, 36(18): 3696-3698. doi: 10.1364/OL.36.003696
[57] Eshniezov B E, Eshchanov B K, Yusupov D B, et al. On the theory of second-harmonic generation in 2D nonlinear photonic crystals with arbitrary domain structures[J]. Physics of Wave Phenomena, 2016, 24(4): 268-271. doi: 10.3103/S1541308X16040038
[58] Mattiucci N, Bloemer M J, D'Aguanno G. Phase-matched second harmonic generation at the Dirac point of a 2-D photonic crystal[J]. Optics Express, 2014, 22(6): 6381-6390. doi: 10.1364/OE.22.006381
[59] Kopylov D A, Svyakhovskiy S E, Dergacheva L V, et al. Observation of optical second-harmonic generation in porous-silicon-based photonic crystals in the Laue diffraction scheme[J]. Physical Review A, 2016, 93(5): 053840. doi: 10.1103/PhysRevA.93.053840
[60] Genereux F, Leonard S W, van Driel H M, et al. Large birefringence in two-dimensional silicon photonic crystals[J]. Physical Review B, 2001, 63(16): 161101. doi: 10.1103/PhysRevB.63.161101
[61] Mandatori A, Sibilia C, Centini M, et al. Birefringence in one-dimensional finite photonic band gap structure[J]. Journal of the Optical Society of America B, 2003, 20(3): 504-513. doi: 10.1364/JOSAB.20.000504
[62] Levy M, Jalali A A. Band structure and Bloch states in birefringent one-dimensional magnetophotonic crystals: an analytical approach[J]. Journal of the Optical Society of America B, 2007, 24(7): 1603-1609. doi: 10.1364/JOSAB.24.001603
[63] Diziain S, Geiss R, Zilk M, et al. Second harmonic generation in free-standing lithium niobate photonic crystal L3 cavity[J]. Applied Physics Letters, 2013, 103(5): 051117. doi: 10.1063/1.4817507
[64] Rivoire K, Lin Ziliang, Hatami F, et al. Second harmonic generation in gallium phosphide photonic crystal nanocavities with ultralow continuous wave pump power[J]. Optics Express, 2009, 17(25): 22609-22615. doi: 10.1364/OE.17.022609
[65] Yamada S, Song B S, Jeon S, et al. Second-harmonic generation in a silicon-carbide-based photonic crystal nanocavity[J]. Optics Letters, 2014, 39(7): 1768-1771. doi: 10.1364/OL.39.001768
[66] Zeng Y, Roland I, Checoury X, et al. Resonant second harmonic generation in a gallium nitride two-dimensional photonic crystal on silicon[J]. Applied Physics Letters, 2015, 106(8): 081105. doi: 10.1063/1.4913679
[67] Kleinman D A. Nonlinear dielectric polarization in optical media[J]. Physical Review, 1962, 126(6): 1977-1979. doi: 10.1103/PhysRev.126.1977
[68] Pershan P S. Nonlinear optical properties of solids: energy considerations[J]. Physical Review, 1963, 130(3): 919-929. doi: 10.1103/PhysRev.130.919
[69] D'Aguanno G, Centini M, Scalora M, et al. Photonic band edge effects in finite structures and applications to χ2 interactions[J]. Physical Review E, 2001, 64(1): 016609. doi: 10.1103/PhysRevE.64.016609
[70] Shi Jianping, Luo Xiangang, Chen Xunan, et al. Analysis of optical SHG in photonic crystal consisting of centro-symmetric dielectric[J]. Optics Express, 2004, 12(22): 5307-5313. doi: 10.1364/OPEX.12.005307
[71] Luo Xiangang, Ishihara T. Engineered second harmonic generation in photonic-crystal slabs consisting of centrosymmetric materials[J]. Advanced Functional Materials, 2004, 14(9): 905-912. doi: 10.1002/(ISSN)1616-3028
[72] Galli M, Gerace D, Welna K, et al. Low-power continuous-wave generation of visible harmonics in silicon photonic crystal nanocavities[J]. Optics Express, 2010, 18(25): 26613-26624. doi: 10.1364/OE.18.026613
[73] Soljačić M, Ibanescu M, Johnson S G, et al. Optimal bistable switching in nonlinear photonic crystals[J]. Physical Review E, 2002, 66(5): 055601. https://www.spiedigitallibrary.org/conference-proceedings-of-spie/5625/1/Optimal-bistable-switching-in-photonic-crystals-with-defect-of-nonlinear/10.1117/12.568256.full
[74] Notomi M, Shinya A, Mitsugi S, et al. Optical bistable switching action of Si high-Q photonic-crystal nanocavities[J]. Optics Express, 2005, 13(7): 2678-2687. doi: 10.1364/OPEX.13.002678
[75] Almeida V R, Lipson M. Optical bistability on a silicon chip[J]. Optics Letters, 2004, 29(20): 2387-2389. doi: 10.1364/OL.29.002387
[76] Yang Xiaodong, Husko C, Wong C W, et al. Observation of femtojoule optical bistability involving Fano resonances in high- Q/Vm, silicon photonic crystal nanocavities[J]. Applied Physics Letters, 2007, 91(5): 051113. doi: 10.1063/1.2757607
[77] Zhang Yong, Li Danping, Zeng Cheng, et al. Ultralow power nonlinear response in an Si photonic crystal nanocavity[J]. IEEE Photonics Journal, 2013, 5(4): 6601409. doi: 10.1109/JPHOT.2013.2273734
[78] Zhang Yong, Li Danping, Zeng Cheng, et al. Low power and large modulation depth optical bistability in an Si photonic crystal L3 cavity[J]. IEEE Photonics Technology Letters, 2014, 26(23): 2399-2402. doi: 10.1109/LPT.2014.2358254
[79] Nozaki K, Tanabe T, Shinya A, et al. Sub-femtojoule all-optical switching using a photonic-crystal nanocavity[J]. Nature Photonics, 2010, 4(7): 477-483. doi: 10.1038/nphoton.2010.89
[80] Morita K, Takahashi T, Kanbara T, et al. Large optical Kerr signal of GaAs/AlAs multilayer cavity with InAs quantum dots embedded in strain-relaxed barriers[J]. Physica E: Low-dimensional Systems and Nanostructures, 2010, 42(10): 2505-2508. doi: 10.1016/j.physe.2009.12.035
[81] Lyubchanskii I L, Dadoenkova N N, Zabolotin A E, et al. Optical bistability in one-dimensional magnetic photonic crystal with two defect layers[J]. Journal of Applied Physics, 2008, 103(7): 07B321. doi: 10.1063/1.2832351
[82] Hu Xiaoyong, Jiang Ping, Ding Chengyuan, et al. Picosecond and low-power all-optical switching based on an organic photonic-bandgap microcavity[J]. Nature Photonics, 2008, 2(3): 185-189. doi: 10.1038/nphoton.2007.299
[83] Sodagar M, Miri M, Eftekhar A A, et al. Optical bistability in a one-dimensional photonic crystal resonator using a reverse-biased pn-junction[J]. Optics Express, 2015, 23(3): 2676-2685. doi: 10.1364/OE.23.002676
[84] Aas S, Müstecaplıoğlu Ö E. Optical bistability in one-dimensional doped photonic crystals with spontaneously generated coherence[J]. Physical Review A, 2013, 88(5): 053846. doi: 10.1103/PhysRevA.88.053846
[85] Asadpour S H, Solookinejad G, Panahi M, et al. Managing optical bistability and multistability by embedding quantum dot nanostructures in a photonic crystal[J]. The European Physical Journal Plus, 2016, 131(11): 406. doi: 10.1140/epjp/i2016-16406-x
[86] Moslemi F, Jamshidi-Ghaleh K. Electrically tunable optical bistability based on one-dimensional photonic crystals with nonlinear nanocomposite materials[J]. Journal of Applied Physics, 2016, 119(9): 093101. doi: 10.1063/1.4942866
[87] 李淳飞.光学双稳态研究20年[J].物理, 1996, 25(5): 267-272. https://www.wenkuxiazai.com/doc/c1611a460912a21614792978-2.html
[88] 龚旗煌.超快速低功率光子晶体全光开关研究进展[J].中国基础科学, 2009, 11(1): 13-15. http://d.old.wanfangdata.com.cn/Periodical/zgjckx200901005
Gong Qihuang. Progress of ultrafast low-power photonic crystal all-optical switching[J]. China Basic Science, 2009, 11(1): 13-15. http://d.old.wanfangdata.com.cn/Periodical/zgjckx200901005
[89] Nozaki K, Lacraz A, Shinya A, et al. All-optical switching for 10-Gb/s packet data by using an ultralow-power optical bistability of photonic-crystal nanocavities[J]. Optics Express, 2015, 23(23): 30379-30392. doi: 10.1364/OE.23.030379
[90] Dolev I, Arie A. Three wave mixing of airy beams in a quadratic nonlinear photonic crystals[J]. Applied Physics Letters, 2010, 97(17): 171102. doi: 10.1063/1.3504247
[91] Kanakis P, Kamalakis T, Sphicopoulos T. Designing photonic crystal waveguides for broadband four-wave mixing applications[J]. Optics Letters, 2015, 40(6): 1041-1044. doi: 10.1364/OL.40.001041
[92] Cerjan A, Raman A, Fan Shanhui. Exceptional contours and band structure design in parity-time symmetric photonic crystals[J]. Physical Review Letters, 2016, 116(20): 203902. doi: 10.1103/PhysRevLett.116.203902
[93] Mock A. Parity-time-symmetry breaking in two-dimensional photonic crystals: square lattice[J]. Physical Review A, 2016, 93(6): 063812. doi: 10.1103/PhysRevA.93.063812
[94] Young A B, Thijssen A C T, Beggs D M, et al. Polarization engineering in photonic crystal waveguides for spin-photon entanglers[J]. Physical Review Letters, 2015, 115(15): 153901. doi: 10.1103/PhysRevLett.115.153901
[95] Matsuda N, Takesue H. Generation and manipulation of entangled photons on silicon chips[J]. Nanophotonics, 2016, 5(3): 440-455. https://www.researchgate.net/publication/304375530_Generation_and_manipulation_of_entangled_photons_on_silicon_chips/fulltext/578e5ad508ae9754b7e9ec54/304375530_Generation_and_manipulation_of_entangled_photons_on_silicon_chips.pdf?inViewer=0&pdfJsDownload=0
-
访问统计


 E-mail Alert
E-mail Alert RSS
RSS

 下载:
下载: