E-mail Alert
RSS
-
摘要
为了实现低温真空环境下红外材料热膨胀系数的高精度测量，提出了一种固体材料低温热膨胀系数的测量方案。本方案基于自准直原理，设计了一种测微结构，建立起了结构变形与角度的关系，并推导出热膨胀系数测量公式。利用测量公式，从理论上分析了该方案的测量误差传递函数关系，并利用误差灵敏度函数对红外材料低温热膨胀系数测量装置的设计精度进行了分析，最后通过计算得到了该方案的测量相对误差。结果表明，测量的热膨胀系数相对误差仅为0.76%，满足纳米级测量要求。
Abstract
In order to realize the high-precision measurement of the thermal expansion coefficient of the infrared material under the cryogenic vacuum environment, a measurement scheme of solid material is proposed. Based on the self-collimation principle, this scheme designs a microstructure, establishes the relationship between structural deformation and angle, and deduces the formula of thermal expansion coefficient measurement. Using the measurement formula, this article analyzes the relationship between the measurement error transfer function of the scheme, and also uses the error sensitivity function to analyze the design accuracy of cryogenic thermal expansion coefficient measuring device for infrared materials, and finally the relative error of the scheme is calculated. The thermal expansion coefficient of the scheme is measured to be only 0.76%, which satisfies the nanometer measurement requirement.
-
Overview
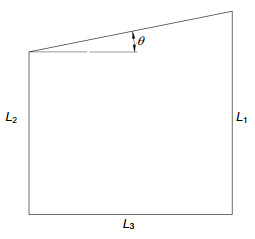
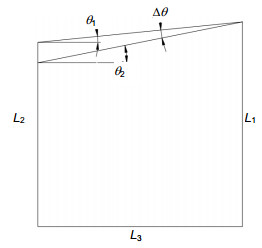
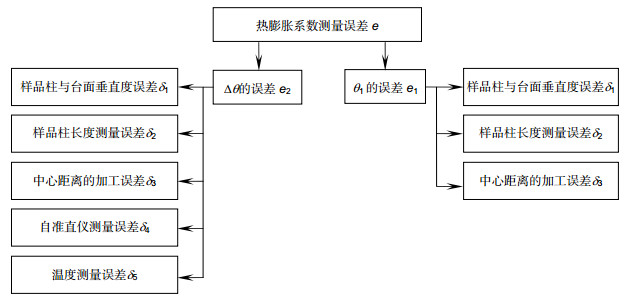
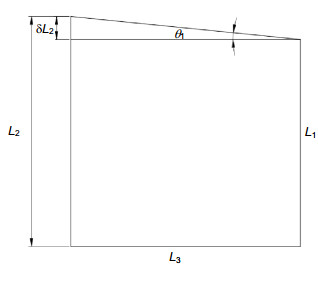
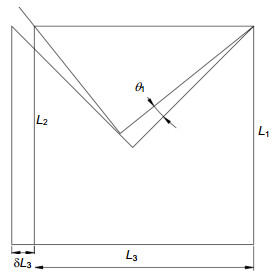
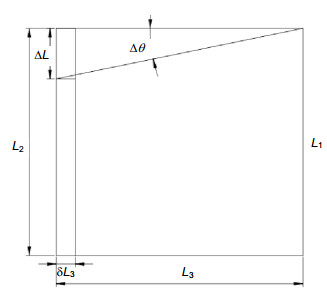
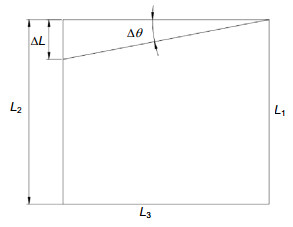
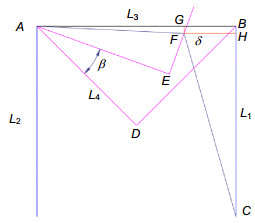
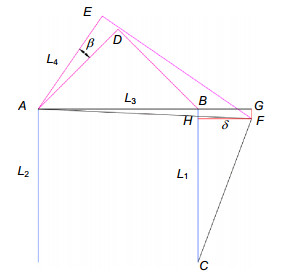
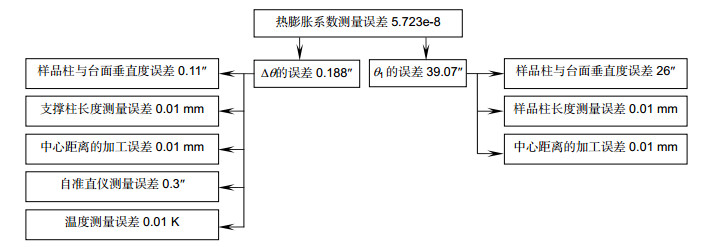
To improve the detection efficiency, the optical components of modern infrared detection system generally need to be cooled. The determination of the thermal expansion coefficient of the infrared material at low temperature can provide the theoretical basis for the study of infrared optical system. Some institutes from home and abroad had researched the thermal expansion coefficient of common solid material in the past. But few people explored the thermal expansion coefficient of infrared materials in low temperature environment. When the infrared material is in minus 250 degrees Celsius, the deformation of material is very small. If the accuracy of the device is not high enough, measurements would become very difficult. So the thermal expansion coefficient of the infrared material is lacking. In order to realize the high-precision measurement of the thermal expansion coefficient of the infrared material under the cryogenic vacuum environment, a measurement scheme of solid material is proposed. Based on the self-collimation principle, this scheme designs a microstructure. The scheme uses a sample column made of infrared material and two support columns to support a plane mirror, and the three cylindrical rods are placed in a triangular manner. A collimator is placed at the top of the plane mirror to measure the angle of the mirror. When the temperature changes, the length of the sample column will change. So the angle of the plane mirror will change. The coefficient of thermal expansion of the solid material is estimated by measuring the angle change of the plane mirror through the collimator. Then the article establishes the relationship between structural deformation and angle, and deduces the formula of thermal expansion coefficient measurement. As the measurement accuracy is relatively high, it is necessary to analyze each error source. In order to calculate the magnitude of the thermal expansion coefficient error, the article calculates the error sensitivity function for each factor and integrates all errors. So using the measurement formula, this article analyzes the error transfer formula theoretically, and also uses the error sensitivity function to analyze the design accuracy of the system. Calculation shows that the effect can be ignored when the squareness tolerance between sample column and the platform reaches 6 levels. Finally, the precision of the scheme is measured to be only 0.76% which satisfies the nanometer measurement requirement. The scheme can achieve not only measurement of thermal expansion coefficient in low-temperature vacuum and high-temperature environments, but also other high-precision nano-sized measurements of linear deformation.
-
-
图 3 样品柱冷却前后反射镜偏转示意图.
Figure 3. The mirror deflection of the sample column before and after cooling.
图 4 热膨胀系数误差源分类.
Figure 4. Classification of error sources of thermal expansion coefficient.
图 10 样品柱向左倾斜反射镜角度变化示意图.
Figure 10. The change of the mirror angle when the sample column is tilted to the left.
图 11 样品柱向右倾斜反射镜角度变化示意图.
Figure 11. The change of the mirror angle when the sample column is tilted to the right.
表 1 一级误差灵敏度
Table 1. Sensitivity of the first order error.
灵敏度类别 S1 S2 灵敏度大小 1.97e-11 4.85e-7 
下载: 导出CSV
表 2 二级误差e1灵敏度
Table 2. Sensitivity of the secondary error e1
灵敏度类别 S1 S2 灵敏度大小 2062.65 2062.85
下载: 导出CSV
表 3 二级误差e2灵敏度
Table 3. Sensitivity of the secondary error e2.
灵敏度类别 S3 S4 S5 灵敏度大小 1.56 -0.008 -3.92
下载: 导出CSV
表 4 不同公差等级下反射镜位置偏差.
Table 4. Position deviation of reflector at different tolerance levels.
公差等级 0 2 4 6 8 10 12 θ1/(") 0 3 10 26 62 155 413
下载: 导出CSV
表 5 不同公差等级下样品柱冷却后反射镜向下偏转角度.
Table 5. At different tolerance levels, the reflector deflects downward when the sample column is cooled.
公差等级 0 2 4 6 8 10 12 θ1/(") 393 390 382 367 331 238 -19
下载: 导出CSV
表 6 样品柱向左偏转反射镜角度变化量差值.
Table 6. The difference in the angle of the mirror when the sample column is deflected to the left.
公差等级 偏转角度∆θ(") 绝对误差/(") 0 392.54 0.00 1 392.54 0.00 2 392.55 0.01 3 392.56 0.02 4 392.58 0.04 5 392.6 0.06 6 392.65 0.11 7 392.71 0.17 8 392.79 0.25 9 392.95 0.41 10 393.14 0.60 11 393.52 0.98 12 394.04 1.50
下载: 导出CSV
表 7 样品柱向右偏转反射镜角度变化量差值.
Table 7. The difference in the angle of the mirror when the sample column is deflected to the right.
公差等级 偏转角度∆θ/(") 绝对误差/(") 0 391.79 0.00 1 391.79 0.00 2 391.79 0.00 3 391.80 0.01 4 391.80 0.01 5 391.80 0.01 6 391.80 0.01 7 391.81 0.02 8 391.81 0.02 9 391.82 0.03 10 391.83 0.04 11 391.86 0.07
下载: 导出CSV
-
参考文献
[1] 倪磊, 任栖锋, 廖胜.红外材料低温折射率测量技术研究:不确定度分析[J].光电工程, 2010, 37(10): 77-82. http://www.oejournal.org/J/OEE/Article/Details/A171201000016/CN
Ni Lei, Ren Qifeng, Liao Sheng. Measurement of cryogenic refractive index of ir materials: uncertainty analysis[J]. Opto-Electronic Engineering, 2010, 37(10): 77-82. http://www.oejournal.org/J/OEE/Article/Details/A171201000016/CN
[2] Svensson S P, Sarney W L, Donetsky D, et al. Materials design parameters for infrared device applications based on III-V semiconductors[J]. Applied Optics, 2017, 56(3): B58–B63. doi: 10.1364/AO.56.000B58 http://cn.bing.com/academic/profile?id=1c8036d2dd235cde28a0526569ffc344&encoded=0&v=paper_preview&mkt=zh-cn
[3] Ordu M, Guo J, Pack G N, et al. Nonlinear optics in germanium mid-infrared fiber material: Detuning oscillations in femtosecond mid-infrared[J]. AIP Advances, 2017, 7(9): 095125. doi: 10.1063/1.5003027 https://www.researchgate.net/publication/320090393_Nonlinear_optics_in_germanium_mid-infrared_fiber_material_Detuning_oscillations_in_femtosecond_mid-infrared_spectroscopy
[4] Lin H, Chen H, Zheng Y J, et al. Two excellent phase-matchable infrared nonlinear optical materials based on 3D diamond-like frameworks: RbGaSn2Se6 and RbInSn2Se6[J]. Dalton Transactions, 2017, 46(24): 7714–7721. doi: 10.1039/C7DT01384A http://pubs.rsc.org/en/content/articlelanding/2017/dt/c7dt01384a#!
[5] Tang J Y, Xiao Z Y, Xu K K. Broadband ultrathin absorber and sensing application based on hybrid materials in infrared region[J]. Plasmonics, 2017, 12(4): 1091–1098. doi: 10.1007/s11468-016-0362-7 https://link.springer.com/article/10.1007/s11468-016-0362-7
[6] Guo S P, Chi Y, Guo G C. Recent achievements on middle and far-infrared second-order nonlinear optical materials[J]. Coordination Chemistry Reviews, 2017, 355: 44–57. http://cn.bing.com/academic/profile?id=cfadaad3a9d2462f6d251aa3d9455407&encoded=0&v=paper_preview&mkt=zh-cn
[7] Bureau B, Boussard-Plédel C, Troles J, et al. Development of optical fibers for mid-infrared sensing: state of the art and recent achievements[J]. Proceedings of SPIE, 2015, 9507: 950702. doi: 10.1117/12.2181952 http://cn.bing.com/academic/profile?id=d1502aa9ad267fab64695cce0ba728a3&encoded=0&v=paper_preview&mkt=zh-cn
[8] Wang Y, Overvig A C, Shrestha S, et al. Tunability of indium tin oxide materials for mid-infrared plasmonics applications[J]. Optical Materials Express, 2017, 7(8): 2727–2739. doi: 10.1364/OME.7.002727
[9] Pizetta D C, Mastelaro V R. Building a dilatometer and determining the coefficient of linear thermal expansion[J]. Revista Brasileira De Ensino De Física, 2014, 36: 1313. http://www.scielo.br/scielo.php?script=sci_arttext&pid=S1806-11172014000100013
[10] Kumar V, Sastry B S R. Thermal expansion coefficient of binary semiconductors[J]. Crystal Research and Technology, 2015, 36(6): 565–569. https://www.researchgate.net/publication/229969628_Thermal_Expansion_Coefficient_of_Binary_Semiconductors
[11] Miyazaki H, Ushiroda I, Itomura D, et al. Thermal expansion of NaZr2 (Po4)3 family ceramics in a low-temperature range[J]. Japanese Journal of Applied Physics, 2008, 47(9): 7262–7265. doi: 10.1143/JJAP.47.7262 http://cn.bing.com/academic/profile?id=93f8ad1d874c42cb3974ec2030f7138f&encoded=0&v=paper_preview&mkt=zh-cn
[12] 黄永华, 吴哲, 李晓慈, 等.热膨胀系数简易测量装置研制及若干材料测量[J].化工学报, 2016, 67(S2): 38–45. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=hgsz2016s2006&dbname=CJFD&dbcode=CJFQ
Haung Yonghua, Wu Zhe, Li Xiaoci, et al. Development of simple thermal expansion coefficient measurement apparatus and its application to several materials[J]. CIESC Journal, 2016, 67(S2): 38–45. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=hgsz2016s2006&dbname=CJFD&dbcode=CJFQ
[13] 吴清仁, 文璧璇. SiC材料导热系数和热膨胀系数与温度关系[J].华南理工大学学报(自然科学版), 1996, 24(3): 11–15. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=hnlg603.002&dbname=CJFD&dbcode=CJFQ
Wu Qingren, Wen Bixuan. Studies on temperature dependence of thermal conductivity and linear expansion for SiC material[J]. Journal of South China University of Technology (Natural Science), 1996, 24(3): 11–15. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=hnlg603.002&dbname=CJFD&dbcode=CJFQ
[14] 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 金属材料热膨胀特征参数的测定: GB/T 4339-2008[S]. 北京: 中国标准出版社, 2009.
People's Republic of China General Administration of Quality Supervision, Inspection and Quarantine, China National Standardization Administration Committee. Test methods for thermal expansion characteristic parameters of metallic materials: GB/T 4339-2008[S]. Beijing: China Standard Press, 2009.
-
访问统计
点击扫一扫
图(12)
表(7)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
