E-mail Alert
RSS
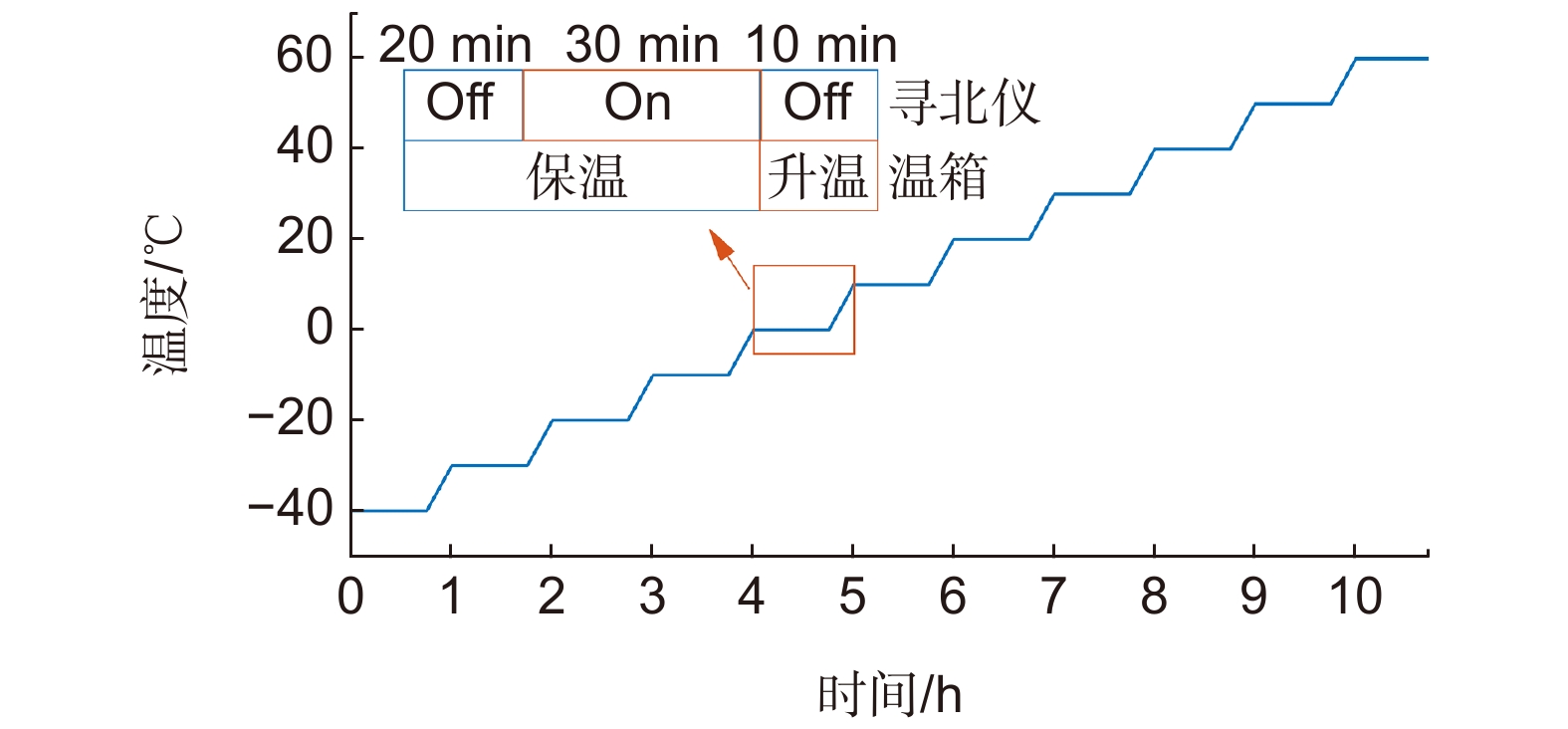
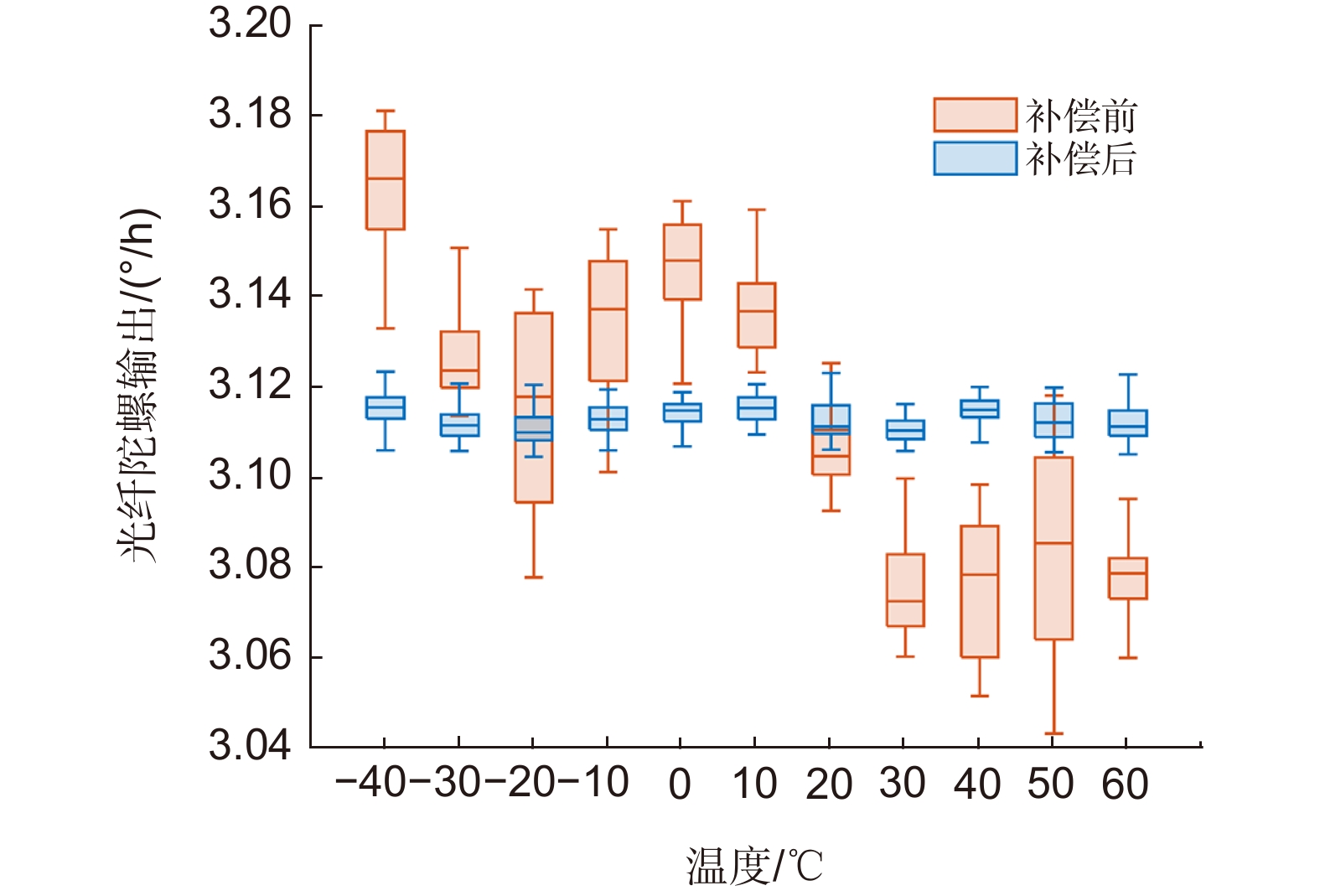
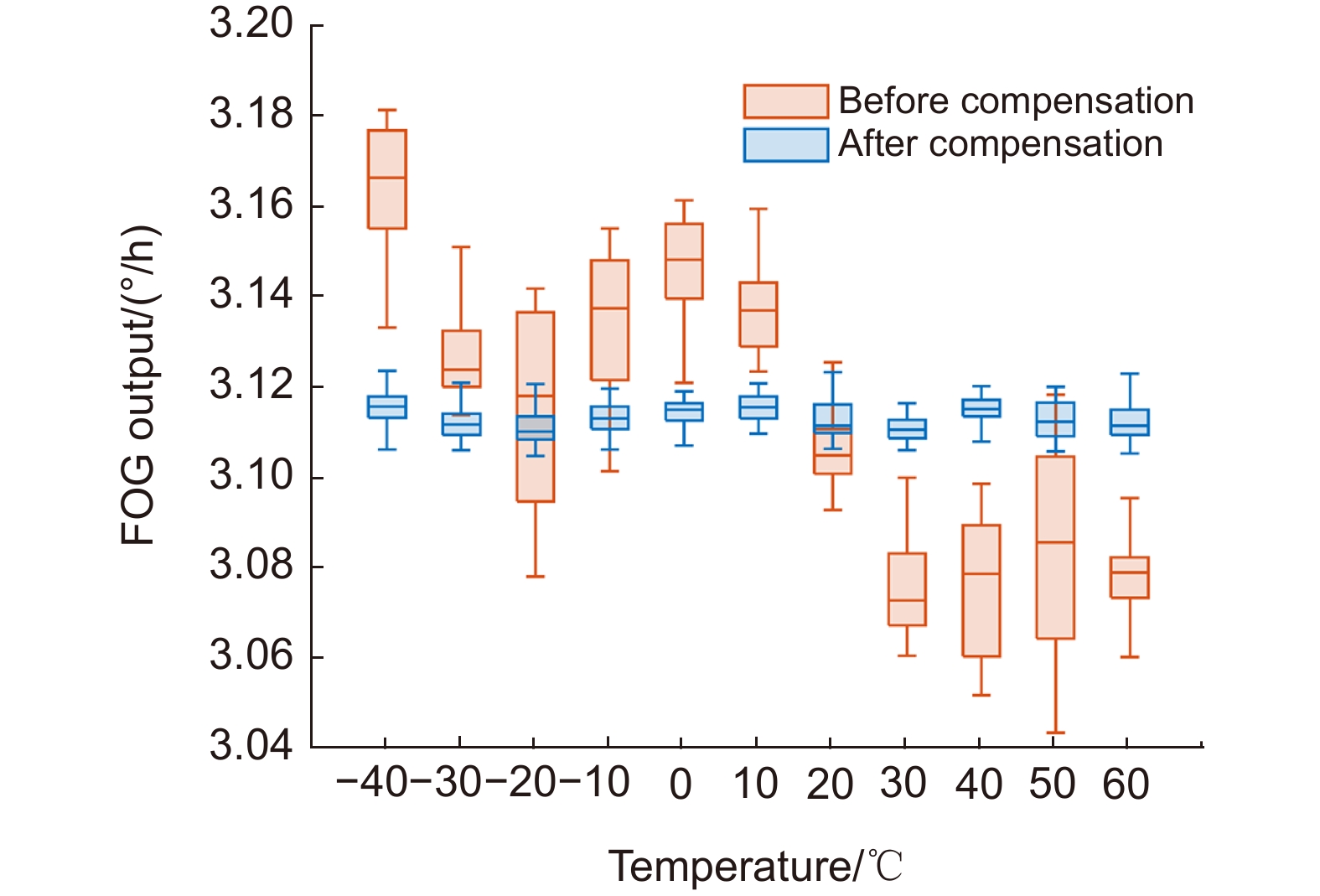
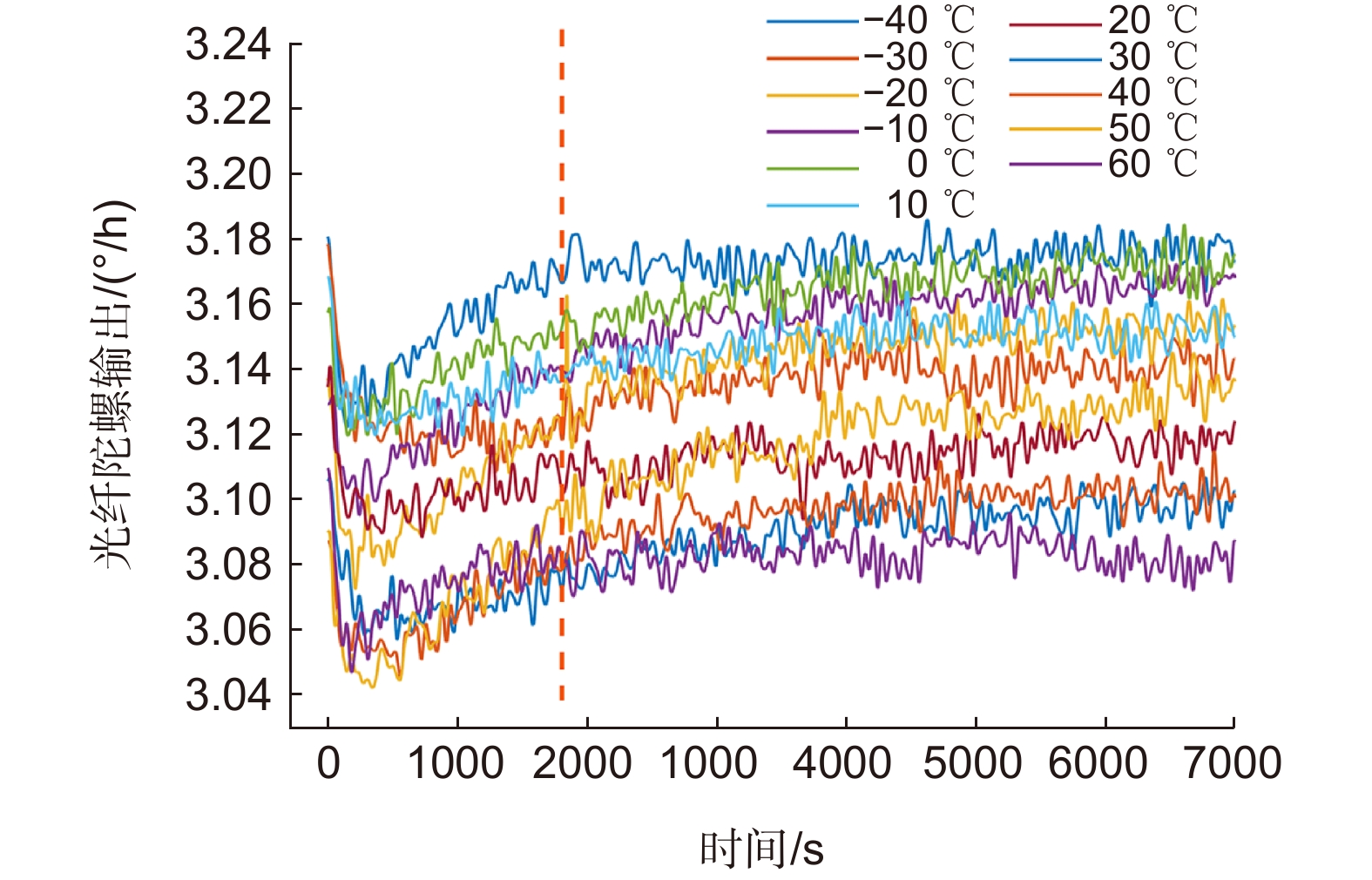
A FOG start-up drift compensation method at full temperatures before and after compensation comparison
-
摘要
本文提出了一种光纤陀螺全温启动温度漂移补偿方法。首先，采用三个惯性传感器内置的温度计信息组成的多维温度变量构建寻北仪内部的温度场，然后使用支持向量回归(SVR)来构建多维温度变量与光纤陀螺温度漂移误差的补偿模型，最后应用麻雀搜索算法(SSA)来调优SVR模型核参数来提高温度误差补偿模型的精度和泛化能力。寻北实验验证了所提方法的有效性：将寻北仪启动阶段的精度从 0.0209°提高到 0.0101°，使其启动阶段的性能与稳定阶段的性能接近，并提升了其在不同初始温度下的快速响应能力。
Abstract
This paper proposes a novel method of compensating for the fiber optic gyroscope (FOG) temperature drift at full temperatures: the temperature field inside the NFS is constructed by multiple temperature variables, which are composed of the thermometer information built in the three inertial sensors, and then the support vector regression (SVR) is used to describe the relationship between the multiple temperature variables and the temperature drift error of the FOG, and finally the sparrow search algorithm (SSA) is applied to tune the model parameters to improve the accuracy and generalization capability. The experimental results validate the effectiveness of the proposed method, and we improve the accuracy of the NFS start-up stage from 0.0209° to 0.0101°. The performance is closely comparable to that of the stable stage, and improves the fast response capability of NFS at different initial temperatures.
-
Overview
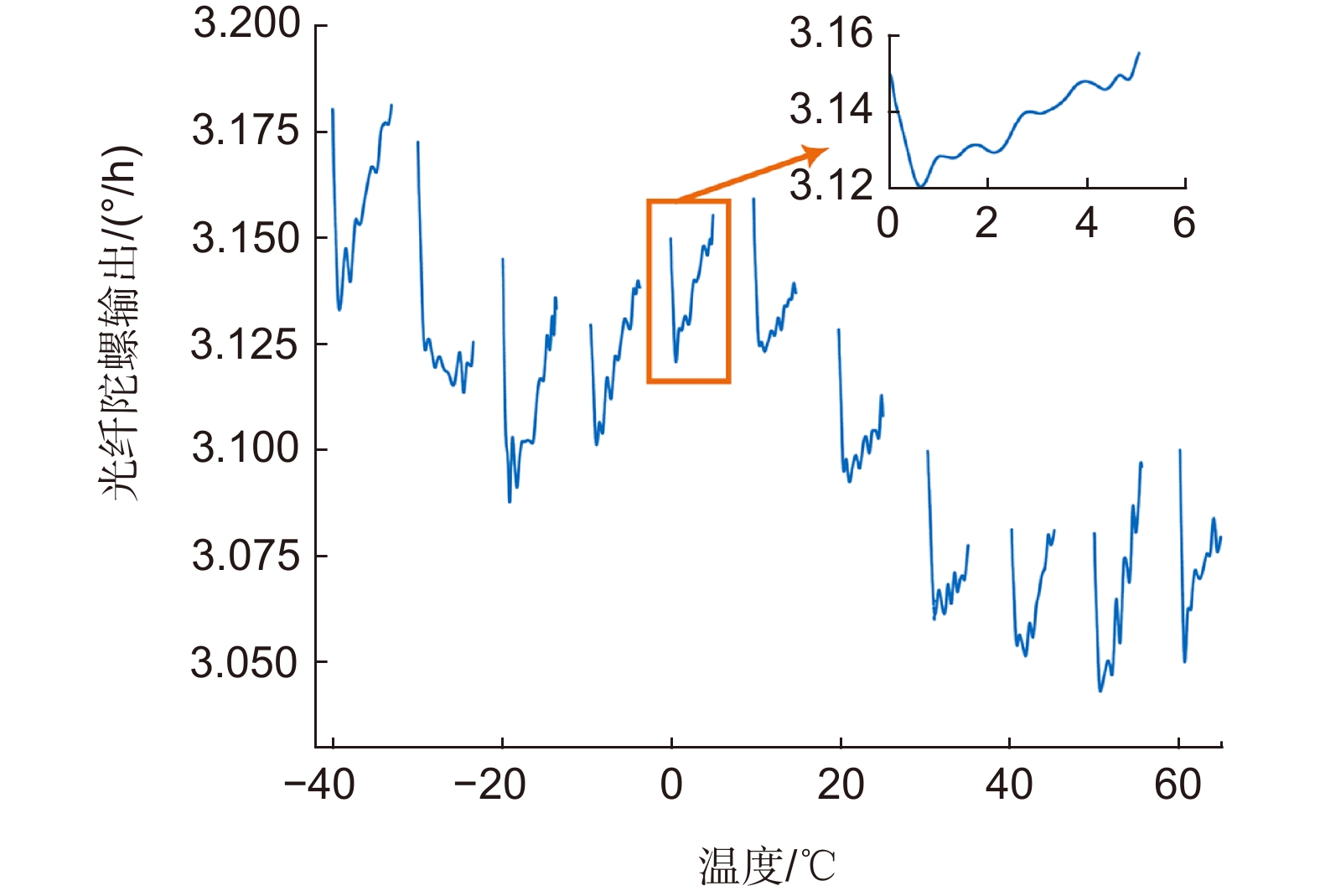
Overview: In the areas of geodesy, mining, and missiles, it is critical to obtain information about the orientation of an object with respect to the geographic coordinate system. A north finding system (NFS) is an instrument that can provide real north orientation, and accuracy and alignment time are two essential parameters of NFS. Shortening the alignment time of NFS can improve the starting speed of weapons and machines. With the advantages of high reliability, low cost, and less environmental requirements, NFS with fiber optic gyroscope (FOG) has become an active trend in inertial technology research. Fiber-NFS consists of a fiber optic gyroscope and two quartz flexible accelerometers (QFAs). However, as the core component of NFS, FOG is susceptible in temperature changes, especially during the start-up stage, the internal units of FOG generate a lot of heat leading to drastic changes in the thermal environment, which will cause the drift error in the output of FOG, and this non-zero mean drift error will greatly affect the accuracy of the system. Traditional compensation methods usually focus on modeling the stable working stage of the FOG, which has limited effectiveness in compensating for the temperature drift during the start-up stage.
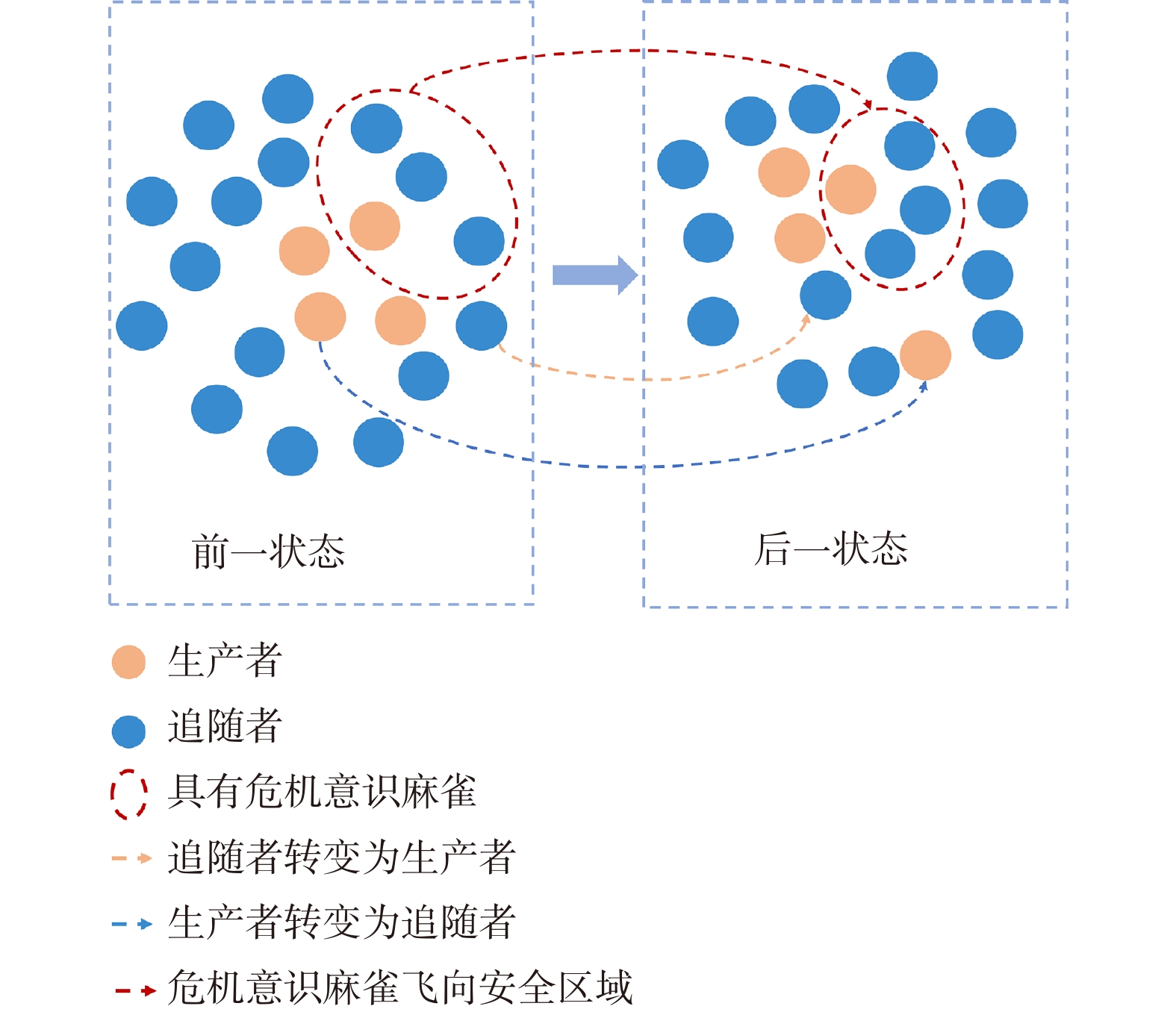
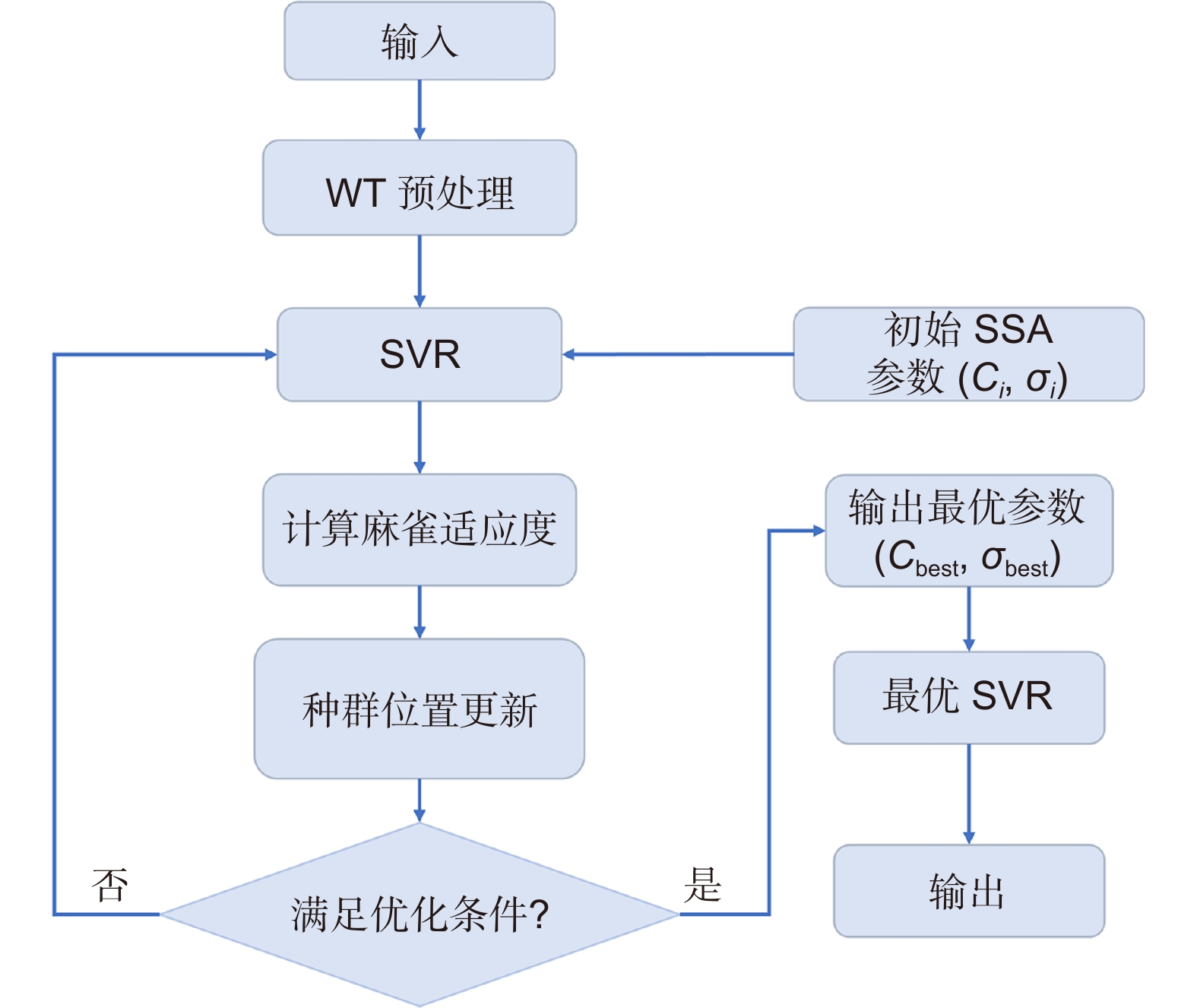
In order to satisfy the requirements of high accuracy and fast response of NFS at different initial temperatures, a novel temperature drift compensation method is proposed in this paper: We combined the information from the built-in thermometers of the three inertial sensors, using their temperature, rate of change of temperature and temperature gradient as input, which provides a more comprehensive description of the complex temperature field inside the NFS. The wavelet transformation (WT) is used to eliminate the non-temperature noise and extract the temperature drift signal accurately, then SVR is used to describe the relationship between multiple temperature variables and drift errors, and finally the accuracy and generalization ability of the model is improved by using the sparrow search algorithm (SSA). The experimental results validate the effectiveness of the proposed method, and we improve the accuracy of the NFS start-up stage from 0.0209° to 0.0101°. The performance is closely comparable to that of the stable stage.
-
-
图 1 不同初始温度下光纤陀螺预处理后的输出
Figure 1. FOG preprocessing outputs at different initial temperatures
图 2 光纤陀螺不同初始温度启动特性
Figure 2. Start-up characteristics of the FOG at different initial temperatures
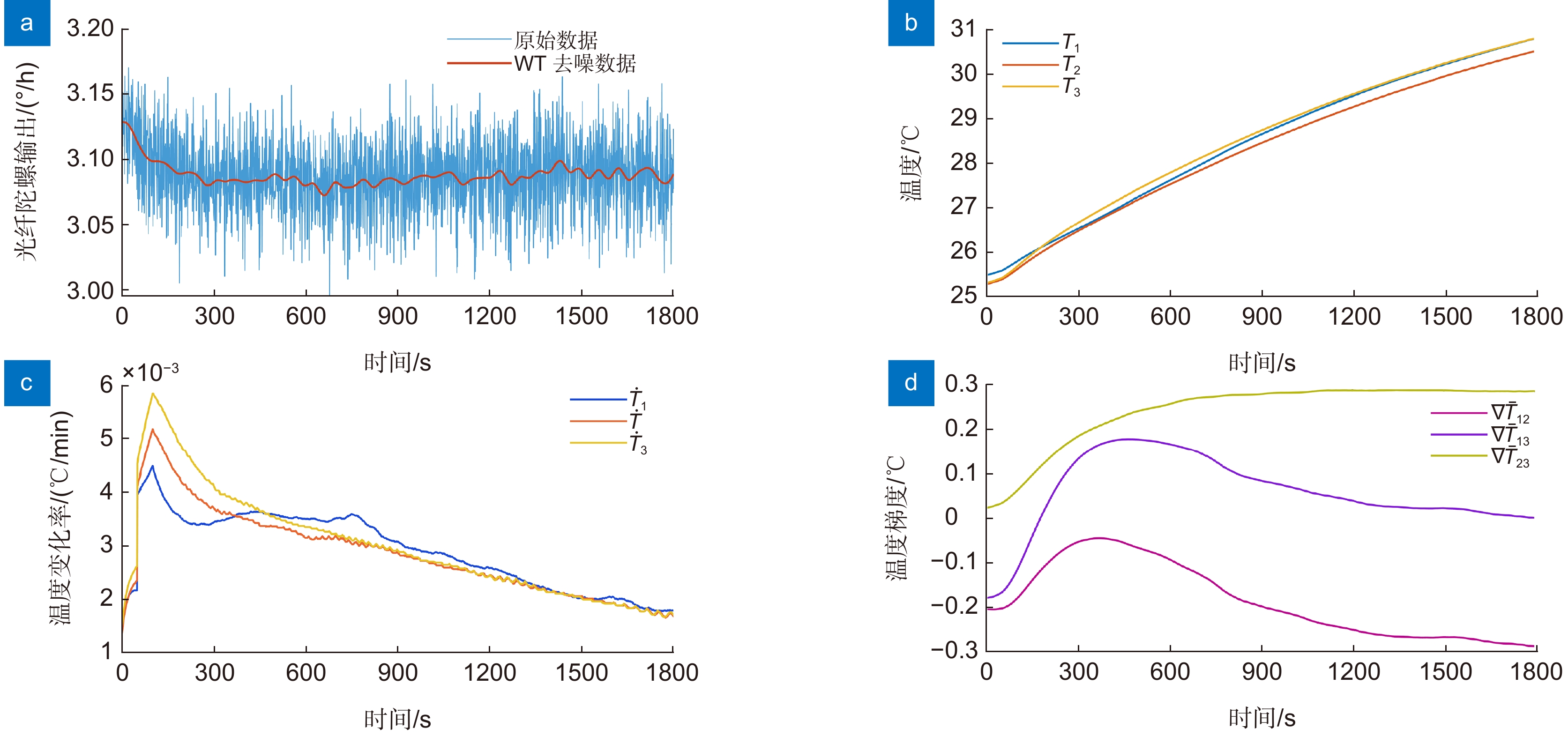
图 3 光纤陀螺输出预处理与寻北仪内部温度信息。(a)光纤陀螺原始输出与小波预处理后的输出；(b)寻北仪内部温度；(c)温度变化率；(d)温度梯度
Figure 3. FOG preprocessing output and NFS internal temperature information. (a) The original output of the FOG and the denoised signal after preprocessing with WT; (b) NFS internal temperature; (c)Temperature ramp; (d)Temperature gradient
表 1 SVR最优核参数
Table 1. Optimal SVR parameters
最优核参数 值 $ {C_{{\rm{best}}}} $ 1.0520 $ {\sigma _{{\rm{best}}}} $ 0.9506 
下载: 导出CSV
表 2 不同算法补偿结果对比
Table 2. Comparison of compensation results of different methods
算法 MAE STD/ (o/h) Denoised data - 0.0134 BP 0.0056 0.0073 SVR 0.0030 0.0035 SSA-SVR 0.0025 0.0031
下载: 导出CSV
表 3 不同算法补偿后寻北均方根误差/(°)对比
Table 3. Comparison of north finding RMSE/(°) of different methods
温度/℃ −32 −16 −5 17 28 43 54 结果均值 补偿前 0.0284 0.0181 0.0216 0.0205 0.0303 0.0171 0.0106 0.0209 BP 0.0284 0.0113 0.0143 0.0137 0.0209 0.0106 0.0100 0.0156 PSO-SVR 0.0146 0.0088 0.0120 0.0144 0.0186 0.0054 0.0060 0.0114 GWO-SVR 0.0110 0.0051 0.0132 0.0093 0.0194 0.0077 0.0096 0.0108 SSA-SVR 0.0113 0.0087 0.0117 0.0131 0.0170 0.0046 0.0045 0.0101
下载: 导出CSV
-
参考文献
[1] Bergh R, Lefevre H, Shaw H. An overview of fiber-optic gyroscopes[J]. J Lightw Technol, 1984, 2(2): 91−107. doi: 10.1109/JLT.1984.1073580
[2] Bojja J, Collin J, Kirkko-Jaakkola M, et al. Compact north finding system[J]. IEEE Sens J, 2016, 16(8): 2554−2563. doi: 10.1109/JSEN.2016.2518860
[3] Arditty H J, Lefèvre H C. Sagnac effect in fiber gyroscopes[J]. Opt Lett, 1981, 6(8): 401−403. doi: 10.1364/OL.6.000401
[4] Shupe D M. Thermally induced nonreciprocity in the fiber-optic interferometer[J]. Appl Opt, 1980, 19(5): 654−655. doi: 10.1364/AO.19.000654
[5] He C H, Yang C C, Wang X Y, et al. Enhanced multiposition method to suppress the north finding error caused by bias drift with fiber optic gyroscopes[J]. Appl Opt, 2013, 52(21): 5303−5311. doi: 10.1364/AO.52.005303
[6] Terrel M A, Digonnet M J F, Fan S H. Resonant fiber optic gyroscope using an air-core fiber[J]. J Lightw Technol, 2011, 30(7): 931−937. doi: 10.1109/JLT.2011.2177959
[7] 李绪友, 张春梅, 刘华兵, 等. 光纤环十六极对称绕法温度性能的仿真与分析[J]. 中国惯性技术学报, 2016, 24(6): 780−785. doi: 10.13695/j.cnki.12-1222/o3.2016.06.015
Li X Y, Zhang C M, Liu H B, et al. Simulation and analysis on temperature performance of fiber ring by 16-polar symmetrical winding method[J]. J Chin Inertial Technol, 2016, 24(6): 780−785. doi: 10.13695/j.cnki.12-1222/o3.2016.06.015
[8] 骆金辉, 周一览, 刘承, 等. 一种应用于光纤陀螺寻北的温度漂移补偿方法[J]. 光电工程, 2020, 47(11): 190681. doi: 10.12086/oee.2020.190681
Luo J H, Zhou Y L, Liu C, et al. A temperature drift compensation method applied to fiber optic gyroscope north-seeking[J]. Opto-Electron Eng, 2020, 47(11): 190681. doi: 10.12086/oee.2020.190681
[9] Zhu R, Zhang Y H, Bao Q L. A novel intelligent strategy for improving measurement precision of FOG[J]. IEEE Trans Instrum Meas, 2000, 49(6): 1183−1188. doi: 10.1109/19.893253
[10] Mao N, Xu J N, Li J S, et al. A LSTM-RNN-based fiber optic gyroscope drift compensation[J]. Math Probl Eng, 2021, 2021: 1636001. doi: 10.1155/2021/1636001
[11] Cheng J C, Fang J C, Wu W R, et al. Temperature drift modeling and compensation of RLG based on PSO tuning SVM[J]. Measurement, 2014, 55: 246−254. doi: 10.1016/j.measurement.2014.05.013
[12] Zhao S, Guo C F, Ke C N, et al. Temperature drift compensation of fiber strapdown inertial navigation system based on GSA-SVR[J]. Measurement, 2022, 195: 111117. doi: 10.1016/j.measurement.2022.111117
[13] Zhao X X, Chen G, Liu H, et al. A multivariate temperature drift modeling and compensation method for large-diameter high-precision fiber optic gyroscopes[J]. IEEE Transactions on Instrumentation and Measurement, 2022, 71: 8502912. doi: 10.1109/TIM.2022.3181900
[14] IEEE. IEEE standard for specifying and testing single-axis interferometric fiber optic gyros: 952–2020[S]. IEEE, 2021. https://doi.org/10.1109/IEEESTD.2021.9353434.
[15] Gharehchopogh F S, Namazi M, Ebrahimi L, et al. Advances in sparrow search algorithm: a comprehensive survey[J]. Arch Comput Methods Eng, 2023, 30(1): 427−455. doi: 10.1007/s11831-022-09804-w
[16] Chang C C, Lin C J. LIBSVM: a library for support vector machines[J]. ACM Trans Intelli Syst Technol, 2011, 2(3): 27. doi: 10.1145/1961189.1961199
[17] Xue J K, Shen B. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Syst Sci Control Eng, 2020, 8(1): 22−34. doi: 10.1080/21642583.2019.1708830
-
访问统计
点击扫一扫
图(9)
表(3)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
