E-mail Alert
RSS
Study on the charge driven displacement behavior of the actuator of the point ahead angle mechanism of a space gravitational wave telescope
-
摘要
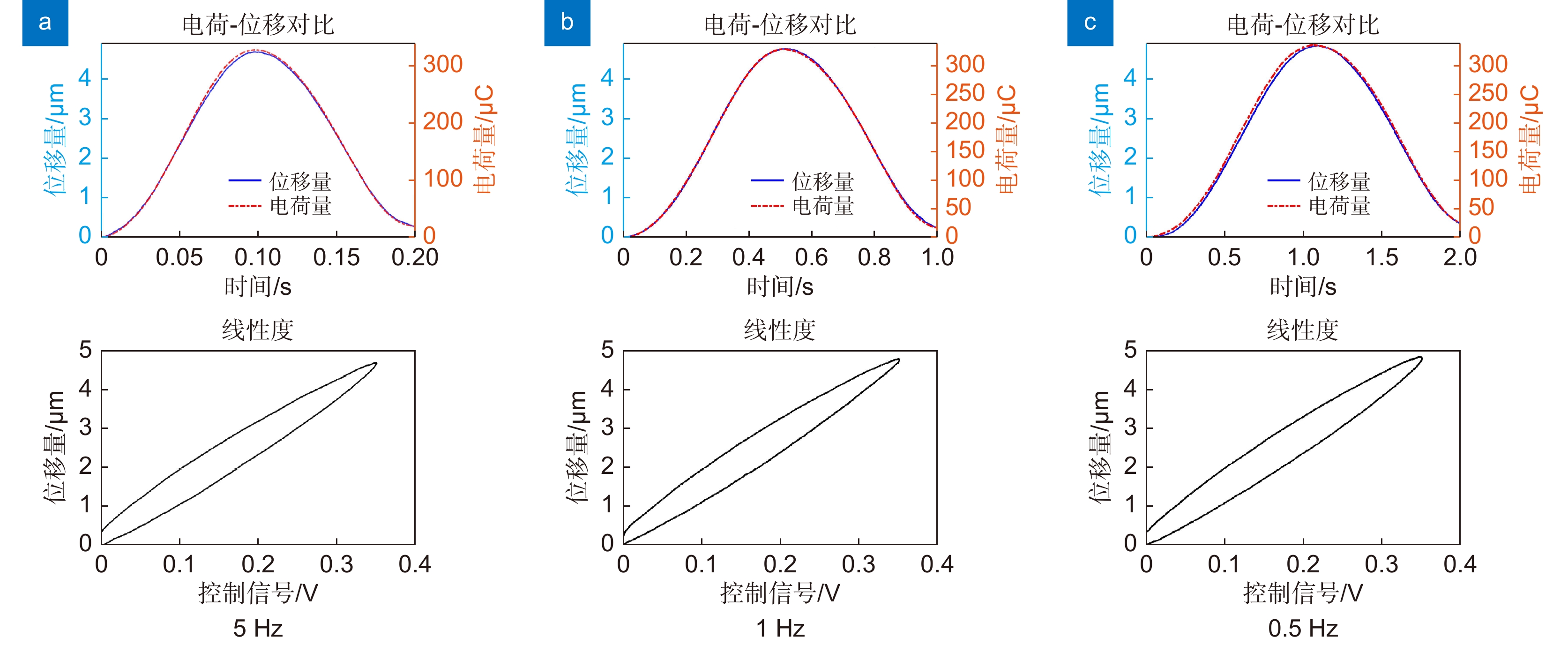
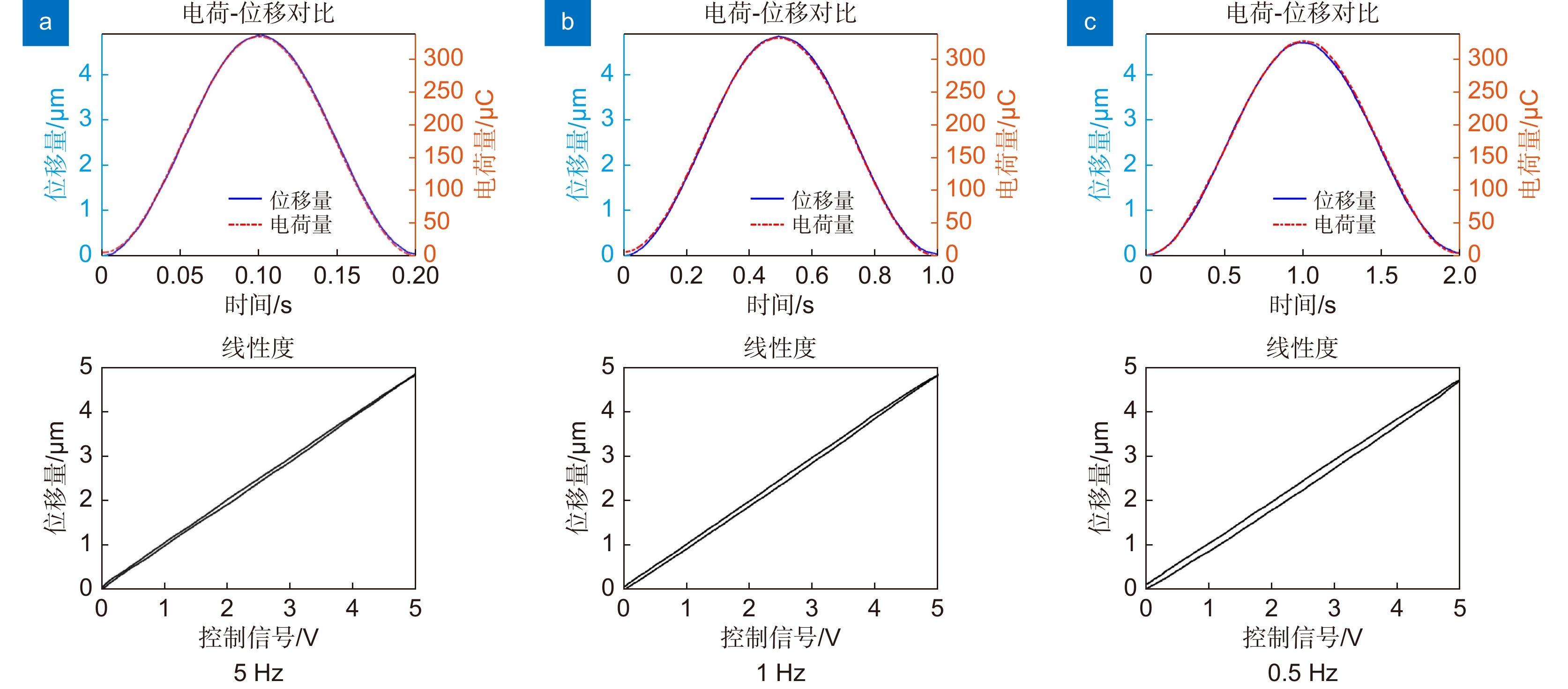
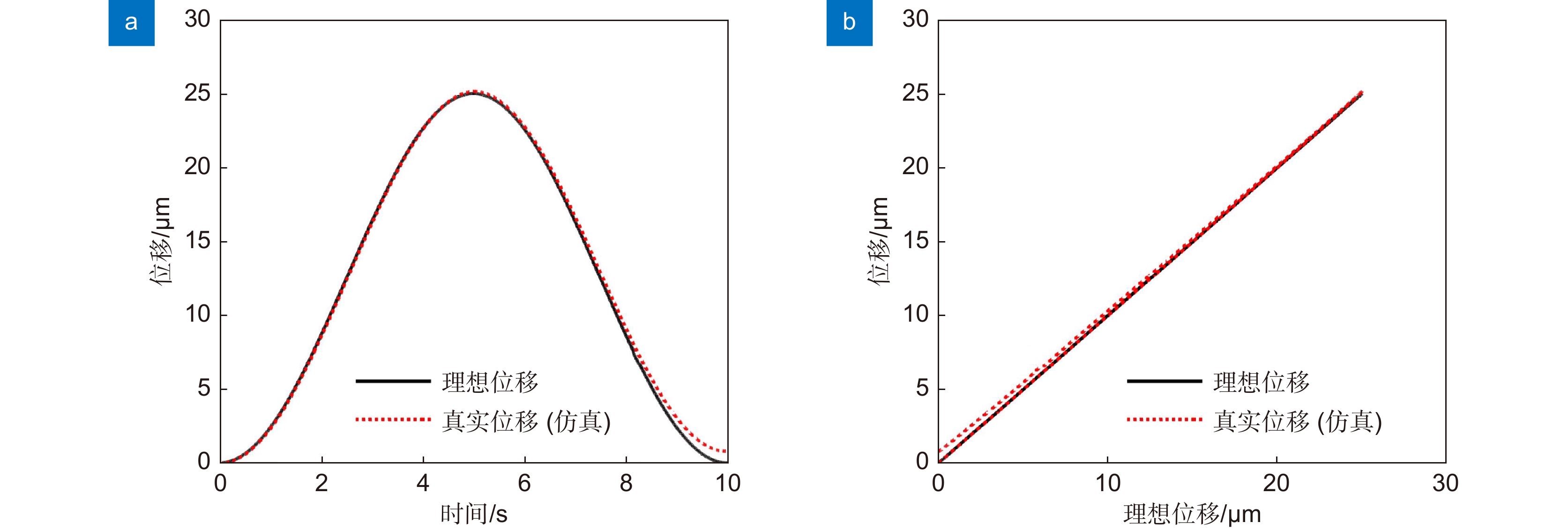
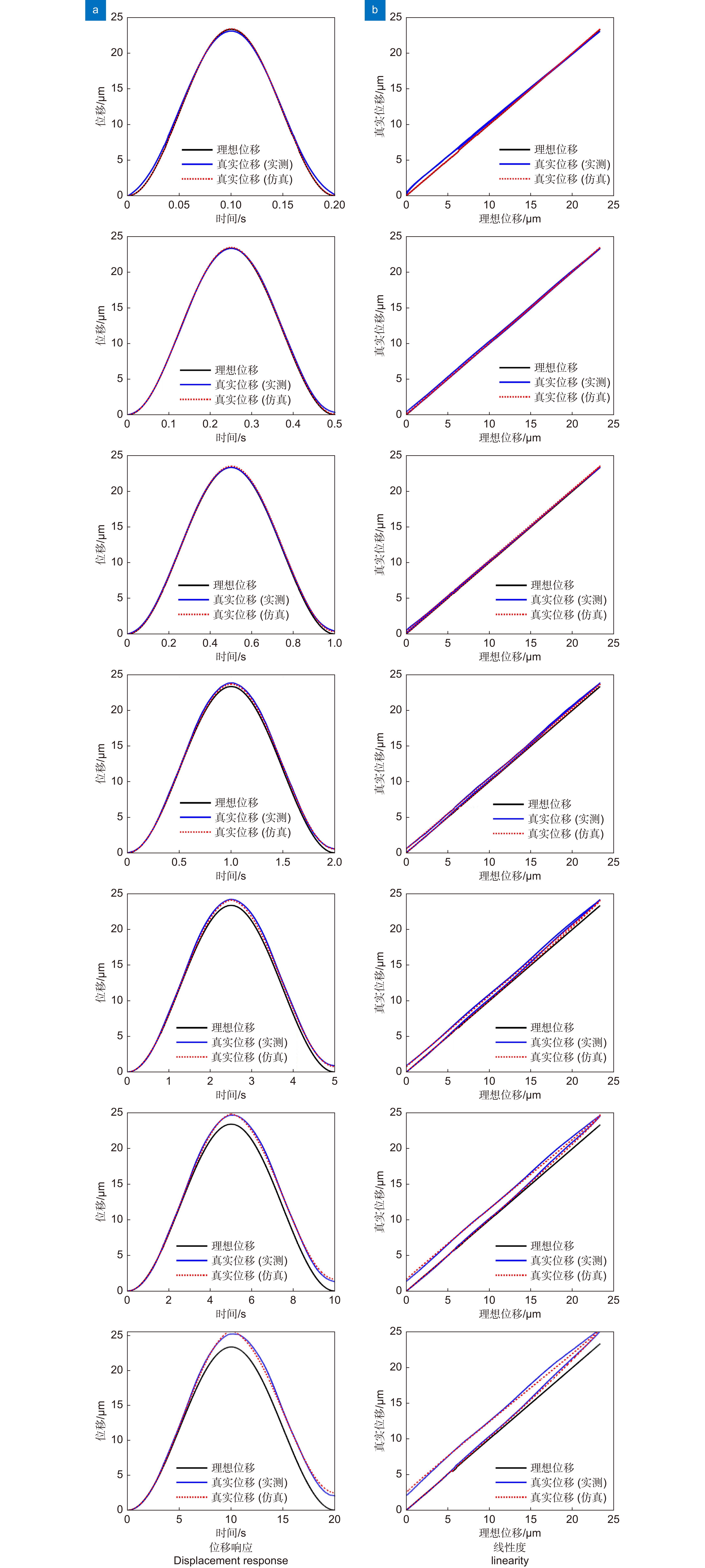
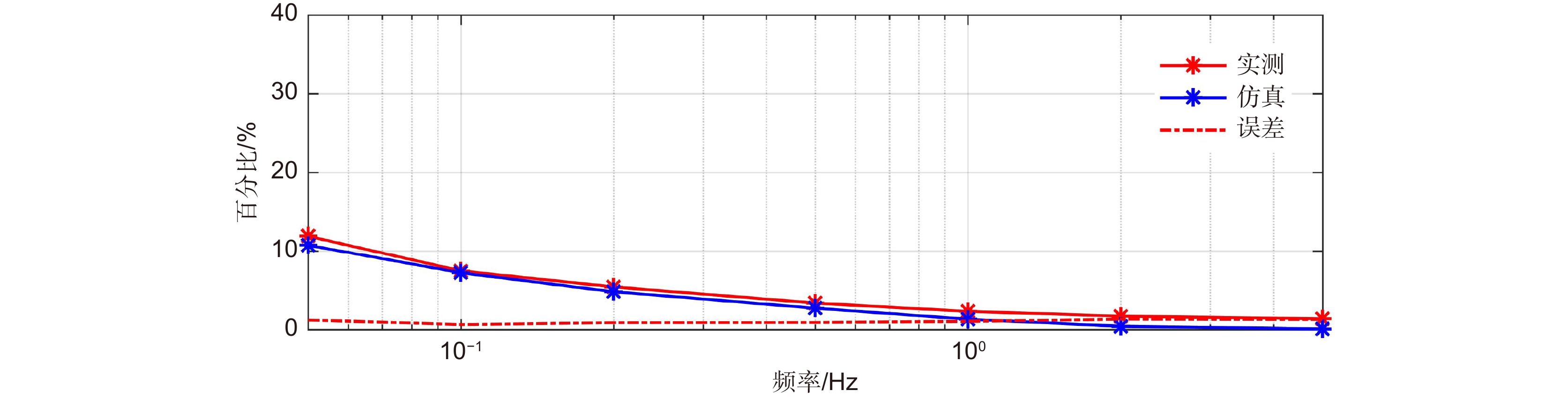
超前瞄准机构(PAAM)是空间引力波探测望远镜的关键部件，其主要通过给压电致动器输入电压或电荷精确控制位移量，实现对望远镜高精度角度控制。因此，压电陶瓷致动器位移响应直接影响超前瞄准机构指向控制性能。本文提出等效电容量计算方法定量分析压电致动器在电荷驱动下的位移响应特性，并通过数值模拟仿真和实验验证等方式验证了计算方法的准确性和可行性。结果表明：在使用幅值5 V、频率0.05 Hz~5 Hz的正弦波信号控制的电荷放大器驱动某型号压电致动器时，采用本文方法分析结果与实验结果相比，二者位移响应最大偏差小于1.35%，为空间引力波探测望远镜超前瞄准机构的高精度指向控制提供了可能的分析方法和实现途径。
Abstract
The point ahead angle mechanism (PAAM) is a key component of the space gravitational wave detection telescope. It can control the displacement of the telescope precisely by inputting voltage or charge to the piezoelectric actuator. Therefore, the displacement response of the piezoelectric ceramic actuator directly affects the pointing control performance of the PAAM. In this paper, the equivalent capacitance calculation method is proposed to quantitatively analyze the displacement response characteristics of piezoelectric actuators driven by charge, and the accuracy and feasibility of the calculation method are verified by numerical simulation and experimental verification. The results show that when a charge amplifier controlled by 5 V, 0.05 Hz~5 Hz sine wave signal is used to drive a certain type of piezoelectric actuator, the maximum deviation of displacement response between the analysis results and the experimental results is within 1.35%, which provides a possible analysis method and realization way for the high-precision pointing control of the PAAM of the space gravitational wave detection telescope.
-
Overview
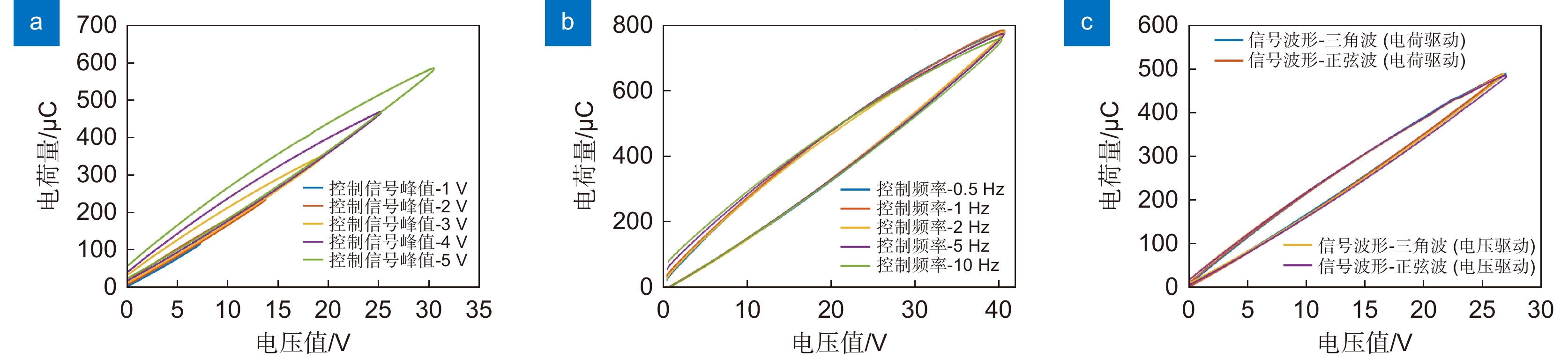
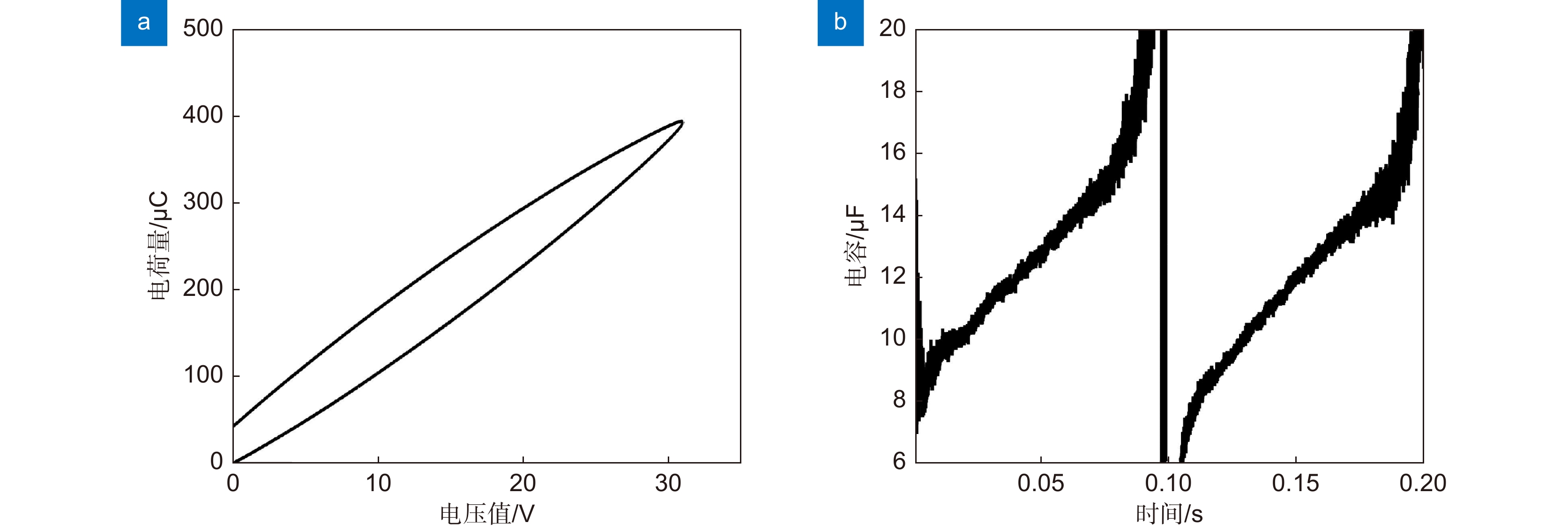
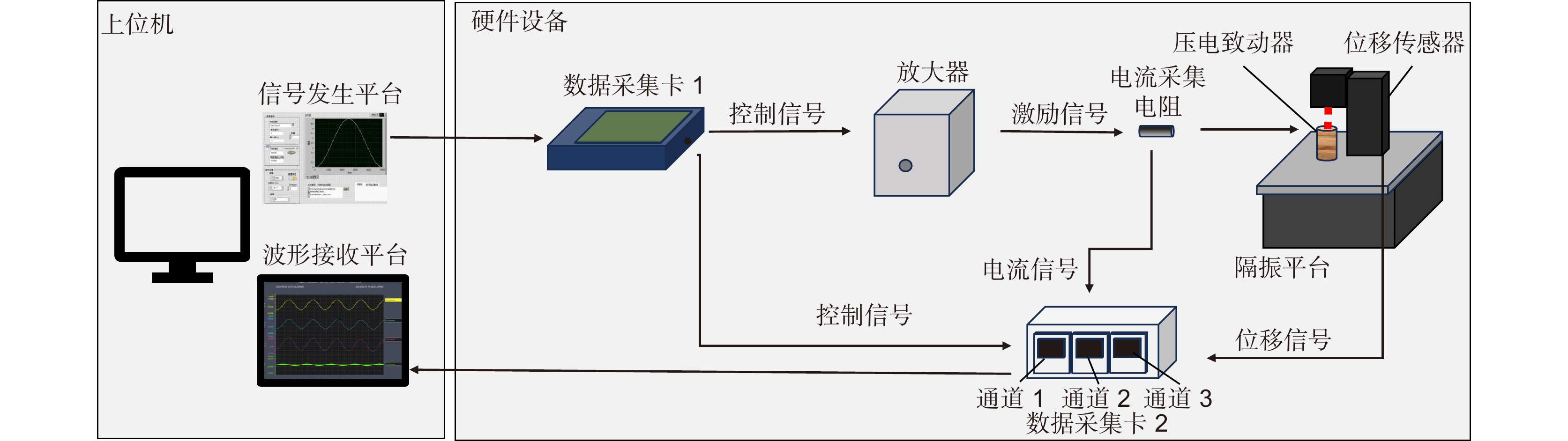
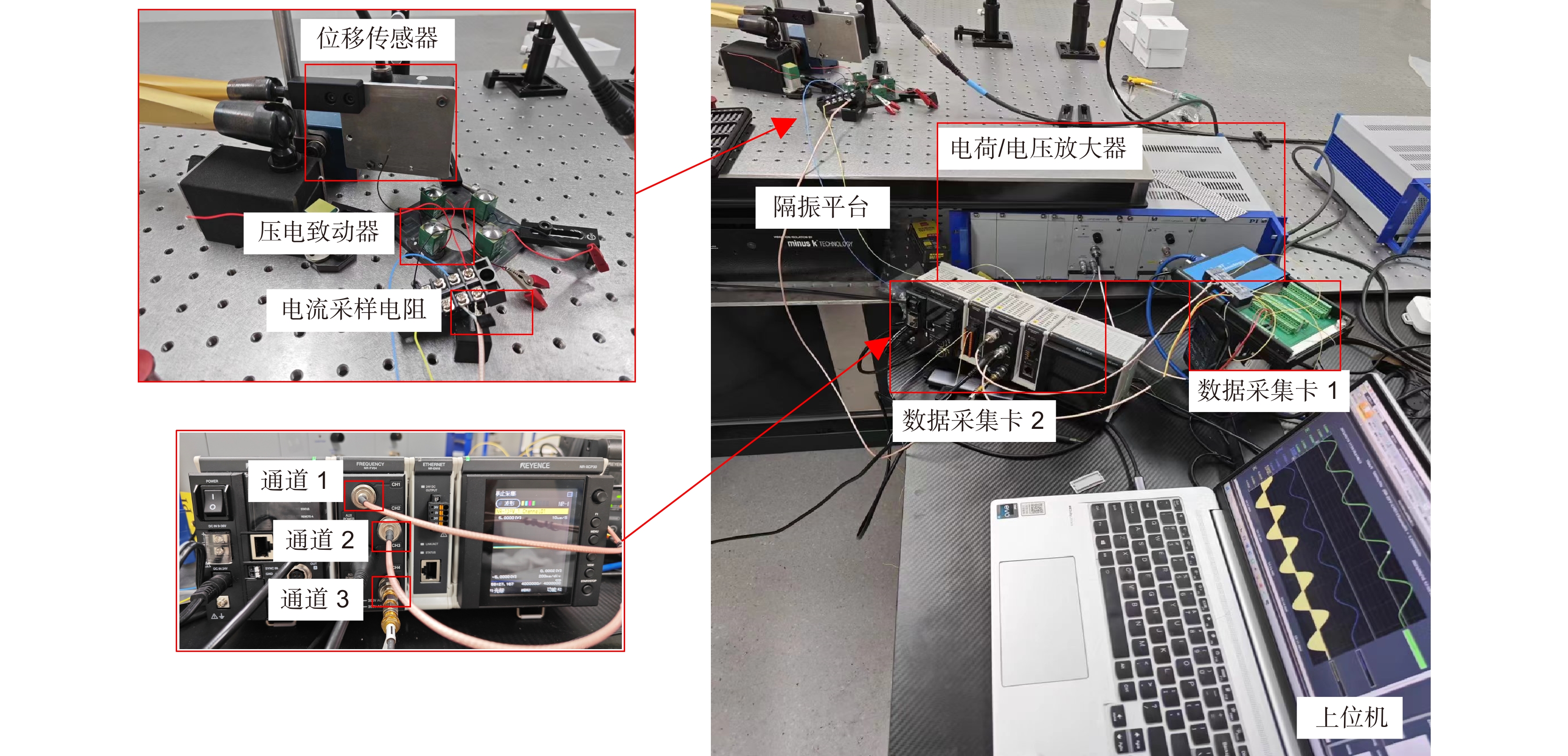
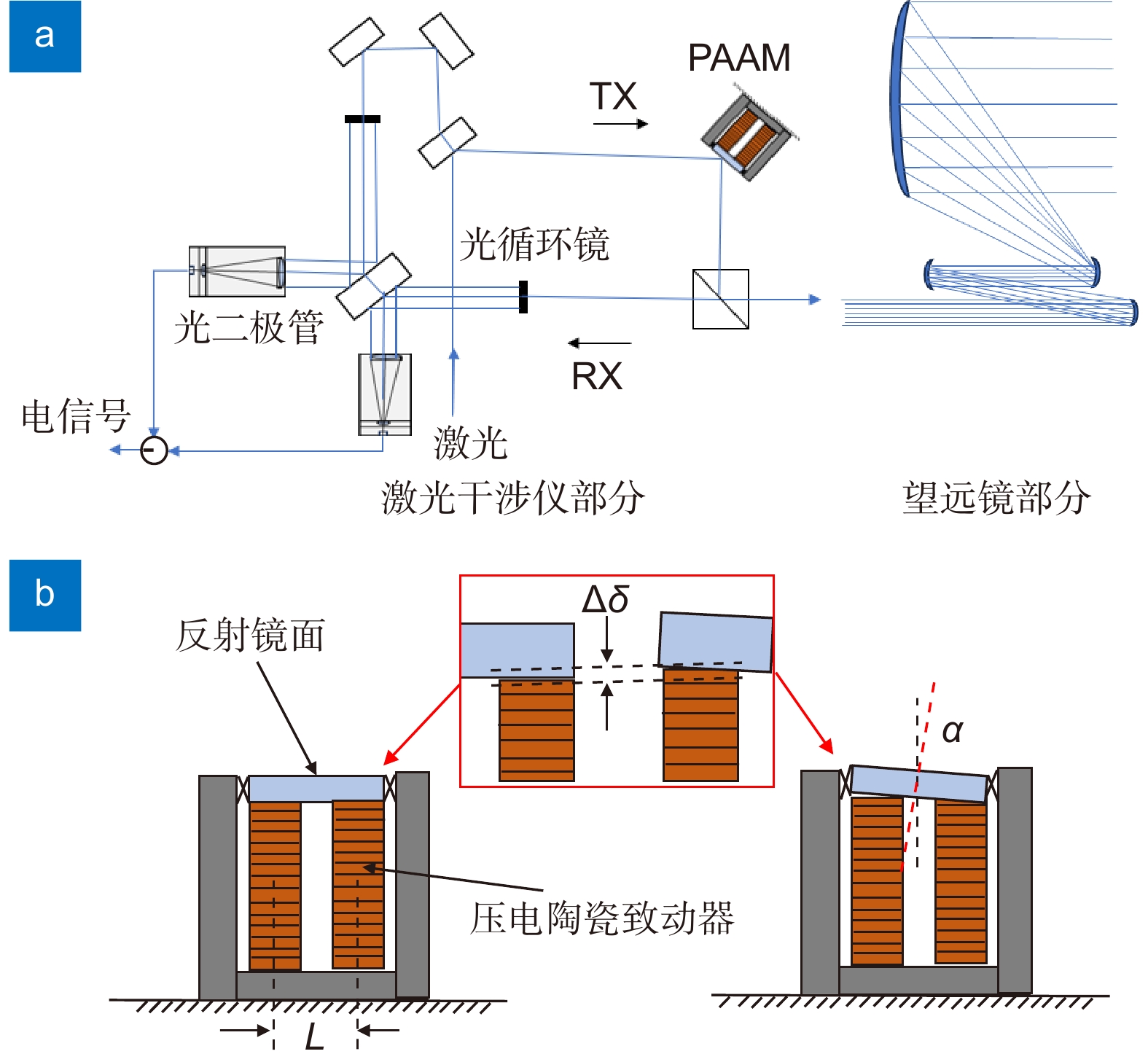
Overview: In the space gravitational wave telescope, the Point Ahead Angle Mechanism (PAAM) is the essential core device to realize ultra-long beam distance measurement and nrad/Hz1/2 level ultra-high precision pointing control. The Piezoelectric Actuator (PZA) is the core component of the PAAM, which mainly controls the displacement through the external input voltage or charge, and drives the PAAM to make the laser beam produce a small inclination Angle to realize the high precision Angle control of the spaceborne telescope. Therefore, the displacement response of piezoelectric ceramic actuators directly affects the pointing control performance of the PAAM. However, the inherent hysteresis of piezoelectric materials causes the linearity of the displacement response of PZA to deteriorate, which makes it difficult to control the direction of the PAAM. In order to realize the high linearity drive of PZA, the charge drive method is worth trying. This paper studies the response behavior of PZA driven by charge. In order to verify the advantage of the charge-driven method in improving the linearity of the displacement response of PZA, the comparison of the charge-driven method with the voltage-driven method is made. The experimental results show that although the charge-driven method has an advantage in improving the linearity of the displacement response compared with the voltage-driven method, there is still poor linearity at low frequency. In this paper, it is pointed out that the main cause of linearity variation under low-frequency signal is the mismatch of circuit components caused by the change of equivalent capacitance of PZA with the signal. In order to accurately describe the displacement response behavior of PZA under low-frequency signals, this paper proposes a calculation method for the equivalent capacitance of PZA. By fitting the equivalent capacitance, a mathematical model of the displacement response of the PZA under charge driving is established, and the displacement response characteristics of the PZA under charge driving are quantitatively analyzed. The accuracy and feasibility of the calculation method are verified by numerical simulation and experimental verification. The results show that when a charge amplifier controlled by 5 V, 0.05 Hz~5 Hz sine wave signal is used to drive a certain type of piezoelectric actuator, the maximum deviation of displacement response between the analysis results and the experimental results is within 1.35%. Which provides a possible analysis method and realization way for the high-precision pointing control of the Point Ahead Angle Mechanism of the space gravitational wave detection telescope.
-
-
图 1 星载望远镜中超前瞄准机构基本原理。(a) 星载望远镜基本原理；(b) 超前瞄准机构基本原理
Figure 1. The principle of PAAM in spaceborne telescopes. (a) Basic principle of spaceborne telescope; (b) Basic principle of PAAM
图 2 压电陶瓷致动器的(a)电压驱动方式和(b)电荷驱动方式基本电路结构
Figure 2. Basic circuit structures of (a) voltage driving mode and (b) charge driving mode of PZA
图 3 电压驱动下压电致动器位移响应及线性度
Figure 3. Displacement response and linearity of PZA under voltage drive
图 4 电荷驱动下压电致动器位移响应及线性度
Figure 4. Displacement response and linearity of PZA under charge drive
图 5 压电致动器的Q-U映射关系与激励信号的关系。(a) 信号幅值；(b) 信号频率；(c) 信号波形
Figure 5. The relationship between Q-U mapping and excitation signal of PZA. (a) Signal amplitude; (b) Signal frequency; (c) Signal waveform
图 6 压电致动器在正弦信号激励下的(a)电压-电荷映射关系及(b)等效电容变化情况
Figure 6. (a) Voltage-charge mapping relationship and (b) equivalent capacitance variation of PZA under sinusoidal excitation
图 7 (a) 压电致动器的真实位移与理想位移响应及(b)二者线性度
Figure 7. (a) Real displacement and theoretical displacement response of PZA and (b) the linearity of both
图 8 压电致动器位移响应实验平台框图
Figure 8. PZA displacement response experiment platform block diagram
图 9 压电致动器位移响应实验平台实物图
Figure 9. Physical diagram of PZA displacement response experiment platform
图 10 电荷驱动的压电致动器位移响应线性度仿真与实测对比
Figure 10. Comparison between simulation and measurement of linearity of displacement response of charge-driven PZA
图 11 不同信号下电荷驱动的压电致动器位移响应线性度仿真与实测对比
Figure 11. Comparison between simulation and measurement of displacement response linearity of charge-driven PZA under different signals
-
参考文献
[1] Abbott B P, Abbott R, Abbott T D, et al. Observation of gravitational waves from a binary black hole merger[J]. Phys Rev Lett, 2016, 116(6): 061102. doi: 10.1103/PhysRevLett.116.061102
[2] Wanner G. Complex optical systems in space: numerical modelling of the heterodyne interferometry of LISA Pathfinder and LISA[D]. Hannover: Gottfried Wilhelm Leibniz Universität, 2010: 1–106.
[3] Danzmann K. LISA mission overview[J]. Adv Space Res, 2000, 25(6): 1129−1136. doi: 10.1016/S0273-1177(99)00973-4
[4] 罗俊, 艾凌皓, 艾艳丽, 等. 天琴计划简介[J]. 中山大学学报(自然科学版), 2021, 60(1-2): 1−19. doi: 10.13471/j.cnki.acta.snus.2020.12.23.2020B154
Luo J, Ai L H, Ai Y L, et al. A brief introduction to the TianQin project[J]. Acta Sci Nat Univ Sunyatseni, 2021, 60(1-2): 1−19. doi: 10.13471/j.cnki.acta.snus.2020.12.23.2020B154
[5] 罗子人, 张敏, 靳刚, 等. 中国空间引力波探测“太极计划”及“太极1号”在轨测试[J]. 深空探测学报, 2020, 7(1): 3−10. doi: 10.15982/j.issn.2095-7777.2020.20191230001
Luo Z R, Zhang M, Jin G, et al. Introduction of Chinese space-borne gravitational wave detection program "Taiji" and "Taiji-1" satellite mission[J]. J Deep Space Explor, 2020, 7(1): 3−10. doi: 10.15982/j.issn.2095-7777.2020.20191230001
[6] Park I H. Detection of low-frequency gravitational waves[J]. J Korean Phys Soc, 2021, 78(10): 886−891. doi: 10.1007/s40042-021-00118-x
[7] 朱伟舟, 谢永, 贾建军, 等. 空间引力波探测超前瞄准机构研制与测试[J]. 红外与激光工程, 2023, 52(4): 20220423. doi: 10.3788/IRLA20220423
Zhu W Z, Xie Y, Jia J J, et al. Development and test of the Point Ahead Angle Mechanism for space gravitational wave detection[J]. Infrared Laser Eng, 2023, 52(4): 20220423. doi: 10.3788/IRLA20220423
[8] Henein S, Spanoudakis P, Schwab P, et al. Design and development of the point-ahead angle mechanism for the laser interferometer space antenna (LISA)[C]//Proceedings of the 13th European Space Mechanisms & Tribology Symposium, 2009.
[9] Rijnveld N, Pijnenburg J A C M. Picometer stable scan mechanism for gravitational wave detection in space[J]. Proc SPIE, 2010, 7734: 77341R. doi: 10.1117/12.857040
[10] K. Uchino, Piezoelectric Actuators and Ultrasonic Motors. Boston, MA: Kluwer Academic, 1996.
[11] 杨圣, 江兵, 周波. 大驱动力高刚度纳米致动新原理研究[J]. 微细加工技术, 2003(1): 65−68,72.
Yang S, Jiang B, Zhou B. Research on new mechanism of nanometer actuating with large driving force and high rigidity[J]. Microfabr Technol, 2003(1): 65−68,72.
[12] 周淼磊, 杨志刚, 田彦涛, 等. 压电执行器非线性控制方法研究进展[J]. 压电与声光, 2007, 29(6): 656−659,662. doi: 10.3969/j.issn.1004-2474.2007.06.010
Zhou M L, Yang Z G, Tian Y T, et al. The development on the nonlinear control method of piezoelectric actuator[J]. Piezoelectr Acoustoopt, 2007, 29(6): 656−659,662. doi: 10.3969/j.issn.1004-2474.2007.06.010
[13] Fleming A J. Position sensor performance in nanometer resolution feedback systems[J]. IFAC Proc Vol, 2013, 46(5): 1−6. doi: 10.3182/20130410-3-CN-2034.00010
[14] Clayton G M, Tien S, Leang K K, et al. A review of feedforward control approaches in nanopositioning for high-speed SPM[J]. J Dyn Syst Meas Control, 2009, 131(6): 061101. doi: 10.1115/1.4000158
[15] Bruno L, Maletta C. Real-time calibration of open-loop piezoelectric actuators for interferometric applications[J]. Int J Mech Mater Des, 2008, 4(2): 97−103. doi: 10.1007/s10999-008-9055-5
[16] 高源蓬, 张泉, 李清灵, 等. 压电陶瓷执行器迟滞非线性补偿与最优控制[J]. 仪器仪表学报, 2022, 43(8): 163−172. doi: 10.19650/j.cnki.cjsi.J2209519
Gao Y P, Zhang Q, Li Q L, et al. Hysteresis nonlinear compensation and optimal control of piezoelectric actuators[J]. Chin J Sci Instrum, 2022, 43(8): 163−172. doi: 10.19650/j.cnki.cjsi.J2209519
[17] Iyer R V, Tan X B. Control of hysteretic systems through inverse compensation[J]. IEEE Control Syst, 2009, 29(1): 83−99. doi: 10.1109/MCS.2008.930924
[18] Main J A, Garcia E, Newton D V. Precision position-control of piezoelectric actuators using charge feedback[J]. Proc SPIE, 1995, 2441: 243−254. doi: 10.1117/12.209814
[19] 范纹彤, 赵宏超, 范磊, 等. 空间引力波探测望远镜系统技术初步分析[J]. 中山大学学报(自然科学版), 2021, 60(1-2): 178−185. doi: 10.13471/j.cnki.acta.snus.2020.11.02.2020b111
Fan W T, Zhao H C, Fan L, et al. Preliminary analysis of space gravitational wave detection telescope system technology[J]. Acta Sci Nat Univ Sunyatseni, 2021, 60(1-2): 178−185. doi: 10.13471/j.cnki.acta.snus.2020.11.02.2020b111
[20] Weise D, Marenaci P, Weimer P, et al. Opto-mechanical architecture of the LISA instrument[J]. Proc SPIE, 2017, 10566: 1056611. doi: 10.1117/12.2308192
[21] Kim D, Choi H, Brendel T, et al. Advances in optical engineering for future telescopes[J]. Opto-Electron Adv, 2021, 4(6): 210040. doi: 10.29026/oea.2021.210040
[22] Guo Y M, Chen K L, Zhou J H, et al. High-resolution visible imaging with piezoelectric deformable secondary mirror: experimental results at the 1.8-m adaptive telescope[J]. Opto-Electron Adv, 2023, 6(12): 230039. doi: 10.29026/oea.2023.230039
[23] Li Z L , Jun Y U , Li Z W ,et al. Physical Modeling of Ferroelectric Capacitors[J]. Piezoelectrics & Acoustooptics, 2001.
-
访问统计
下载:
点击扫一扫
图(12)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
