E-mail Alert
RSS
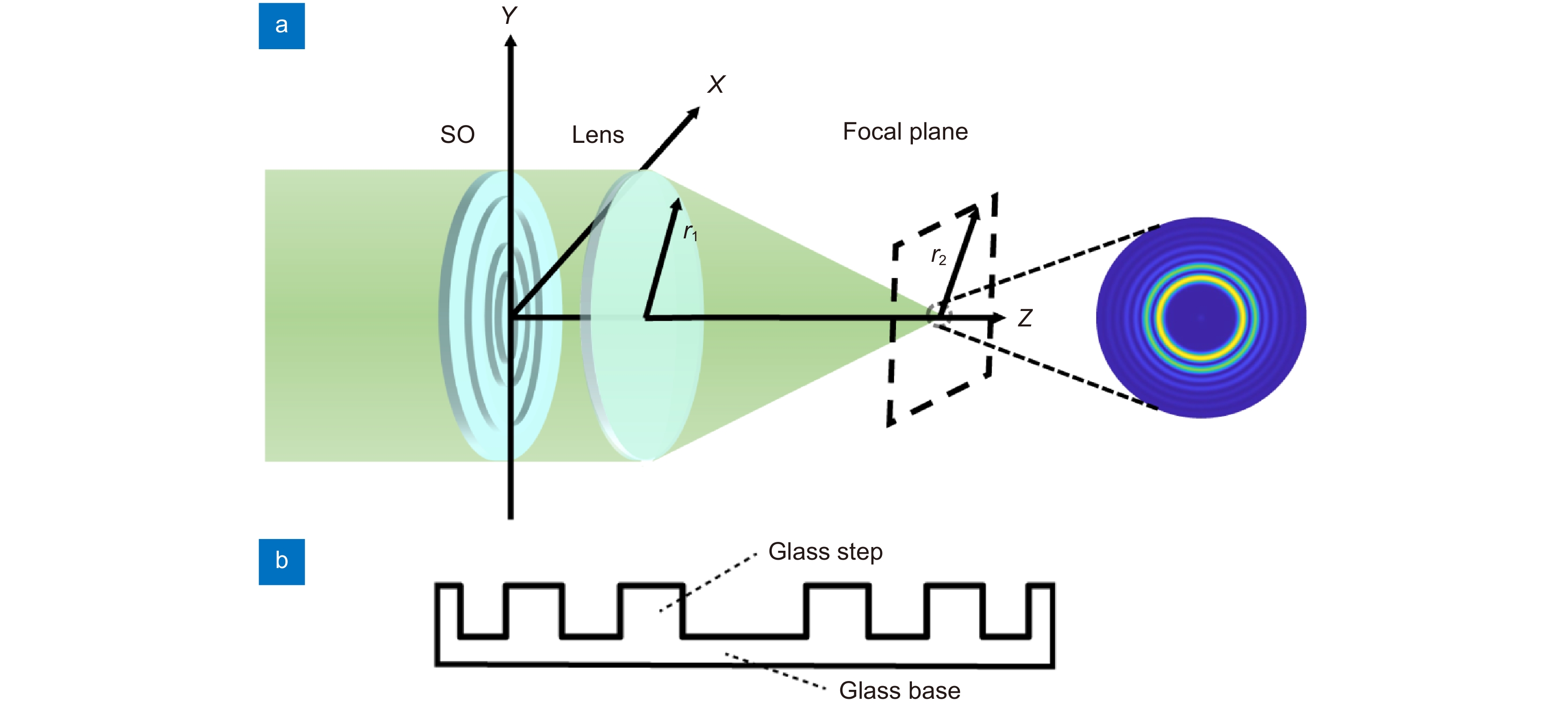
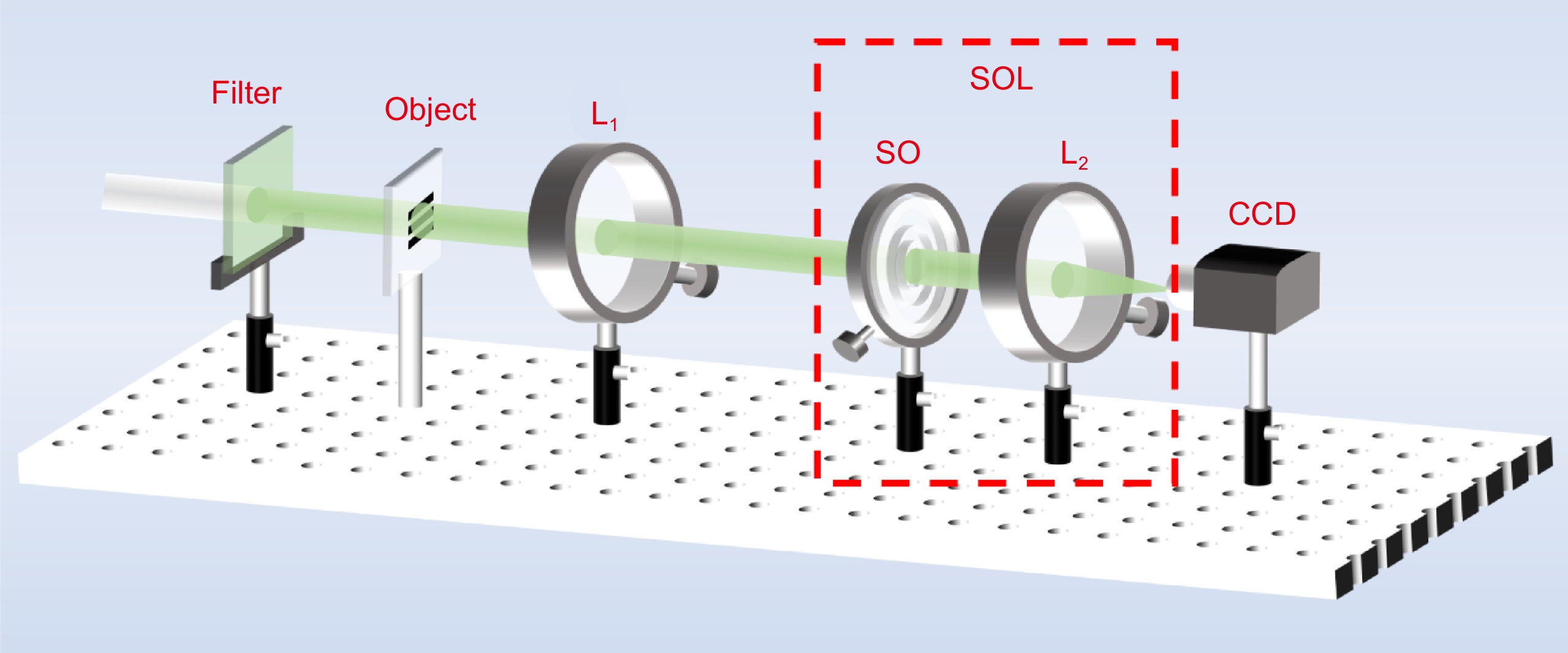
Analysis of spherical aberration effect in super-oscillatory telescopic imaging system
-
摘要:
在超振荡望远系统中，球差是影响其分辨本领的重要因素，其原因在于球差导致强度点扩散函数视场内产生高旁瓣，降低该系统的分辨力。本文分析了超振荡望远系统中球差对成像的影响，并确定了该系统对初级球差的容许范围。基于光学超振荡原理，利用线性规划的优化方法，设计超振荡望远系统，在532 nm工作波长下能够实现0.68倍瑞利判据的分辨力。构建针对超振荡望远系统球差的定量分析数学模型，该系统在均方根(root mean square，RMS)不超过0.041倍波长的初级球差干扰下，能分辨三缝目标物，同时分析了窄带工作波长对于该球差系统带来的成像影响。本文在光学测量、环境监视、超分辨望远等领域具有潜在的应用前景。
Abstract:The spherical aberration is an important factor affecting the resolution power of super-oscillatory telescopic systems. The reason is that the spherical aberration leads to a high sidelobe in the field of view of the intensity point spread function, which reduces the resolution of the system. In this paper, the effect of the spherical aberration on imaging in a super-oscillatory telescopic system is analyzed and the allowable range of the primary spherical aberration is determined. Based on the principle of optical super-oscillatory and the optimization method of linear programming, a super-oscillatory telescopic system is designed. A resolution of 0.68 times the Rayleigh criterion can be achieved under a working wavelength of 532 nm. A mathematical model for quantitative analysis of the super-oscillatory telescopic system with the spherical aberration is established. The system can distinguish the three-slit target under the interference of the primary spherical aberration with a root mean square (RMS) no more than 0.041 times wavelength. The imaging effect of the narrow band working wavelength in the spherical aberration system is analyzed. This paper has potential applications in optical measurement, environmental monitoring, super-resolution telescope, and other fields.
-
Key words:
- super-oscillatory /
- telescopic system /
- spherical aberration /
- Rayleigh criterion
-
Overview: Due to light diffraction, the angular resolution of the telescopic system cannot break through the Rayleigh criterion 1.22λ/D. Super-resolution imaging techniques such as fluorescent microscopy (FM) or Fourier ptychography microscopy (FPM) applied to microscopic systems are difficult to be transplanted to telescopic systems. Using a super-oscillatory lens (SOL) to modulate the light field can compress the focal spot and theoretically realize arbitrarily small light energy convergence. The technique does not require marking the object or a special illuminated light field, therefore, the technique can be applied to a telescopic system to achieve resolution beyond the Rayleigh criterion. In optical systems, the spherical aberration reduces resolution and cannot be completely eliminated. Currently, the effects of the spherical aberration on confocal microscopy (CM), wide-field microscope (WFM), and confocal light sheet microscopy (CLSM) have been reported. There are few reports about the effect of the spherical aberration on the SOL, especially in the field of telescopic imaging. In addition, for the super-oscillatory telescopic system, due to the processing error, it is difficult to reach the theoretical value of correcting spherical aberration. Therefore, it is very important to analyze the influence of the spherical aberration in the super-oscillatory telescopic system and determine the corresponding allowable range of the spherical aberration. In this paper, the effect of the spherical aberration on imaging in a super-oscillatory telescopic system is studied and the allowable range of the primary spherical aberration in the system is calculated. In the field of view of 1.5 times the Rayleigh criterion, the spherical aberration will increse the sidelobe of the intensity point spread function and reduce the resolution of the system. The SOL is the core of a super-oscillatory telescopic system, which is designed based on the Torraldo method in this paper. This method transforms the design problem of the SOL into an optimization problem, and then it becomes a linear programming problem. Optimal parameters of the SOL are received by solving the global optimal solution of linear programming. The maximum resolution of the system is 0.68 times the Rayleigh criterion at the working wavelength of 532 nm. A mathematical model for quantitative analysis of the spherical aberration in a super-oscillatory telescopic system is established. The system maximally allows the primary spherical aberration interference with a root mean square (RMS) of 0.041 times wavelength. At the same time, the influence of the spherical aberration on the imaging of the system under a narrow band is studied. This paper has potential applications in optical measurement, environmental monitoring, super-resolution telescope, and other fields.
-
-
图 1 超振荡望远成像系统示意图
Figure 1. Schematic of the super-oscillatory telescopic imaging system
图 2 (a) SOL压缩强度点扩散函数示意图；(b) SO的径向截面图
Figure 2. (a) Schematic of the SOL compresses the intensity point spread function (PSF); (b) Section of the SO along the diameter direction
图 3 (a) 优化后径向强度点扩散函数；(b) SO的相位调制函数
Figure 3. (a) The intensity PSF along the diameter direction after optimization; (b) Phase modulation function of the SO
图 4 (a) 超振荡望远系统径向强度点扩散函数；(b) RMS值为0.042λ的初级球差分布
Figure 4. (a) The intensity PSF along the diameter direction in the super-oscillatory telescopic system; (b) Distribution of the primary spherical aberration with a RMS value of 0.042λ
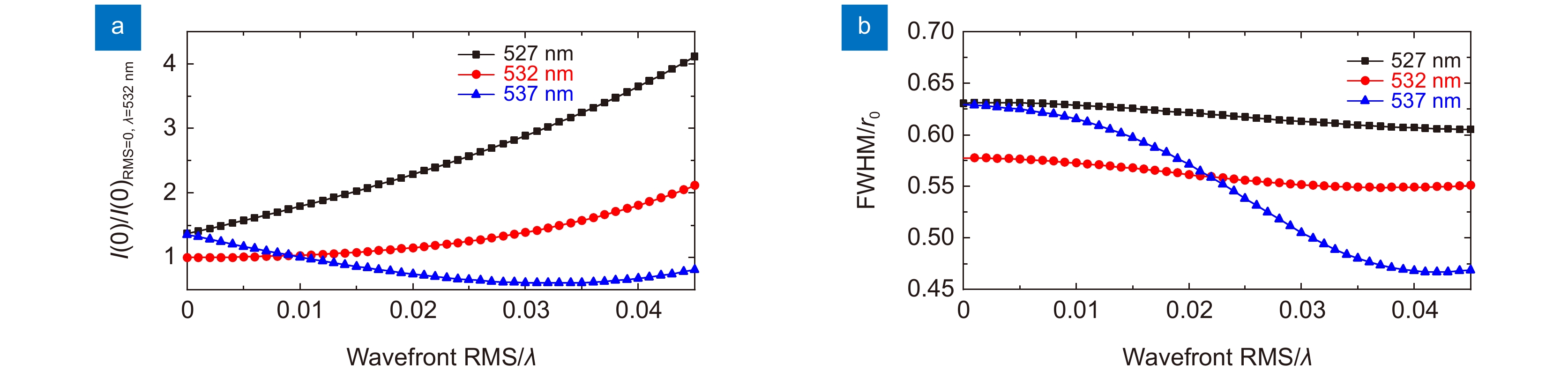
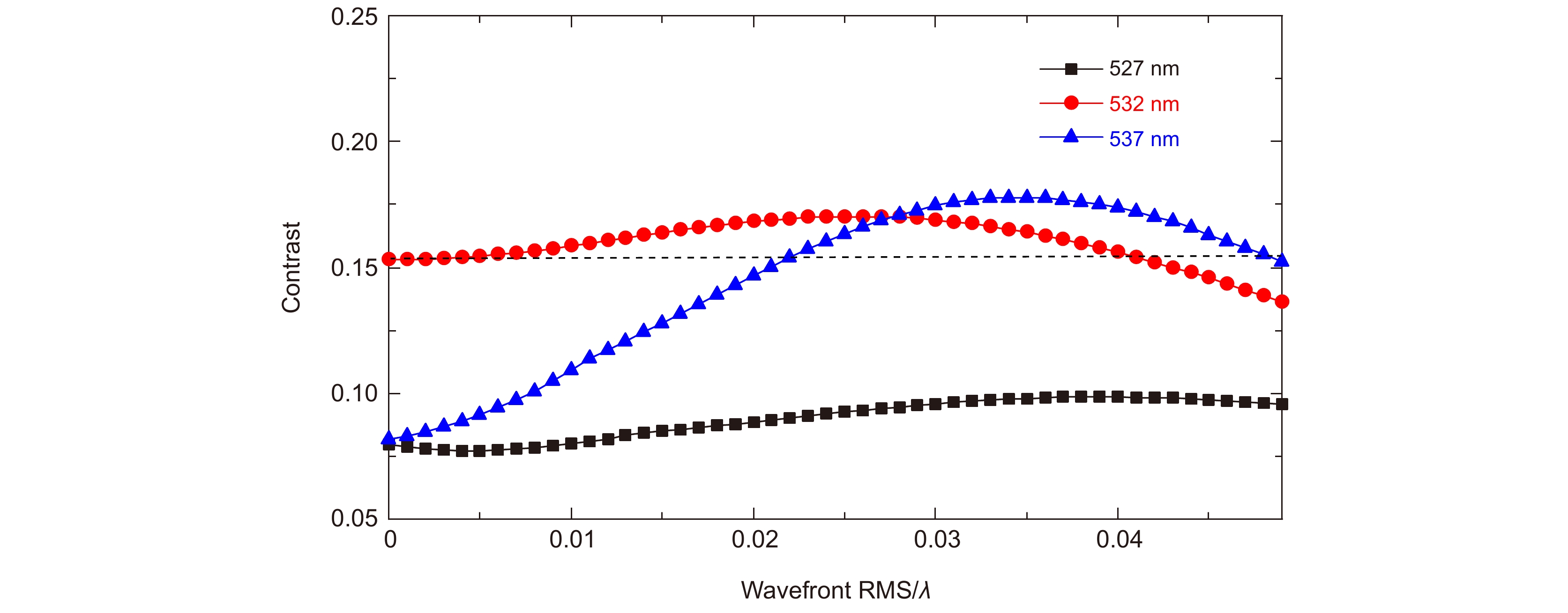
图 5 (a) 不同工作波长，不同初级球差系统强度点扩散函数相对中心值；(b) 不同工作波长，不同初级球差系统FWHM相对值
Figure 5. (a) Relative central values of the intensity PSF in different primary spherical aberration systems under different working wavelengths; (b) Relative values of FWHM in different primary spherical aberration systems under different working wavelengths
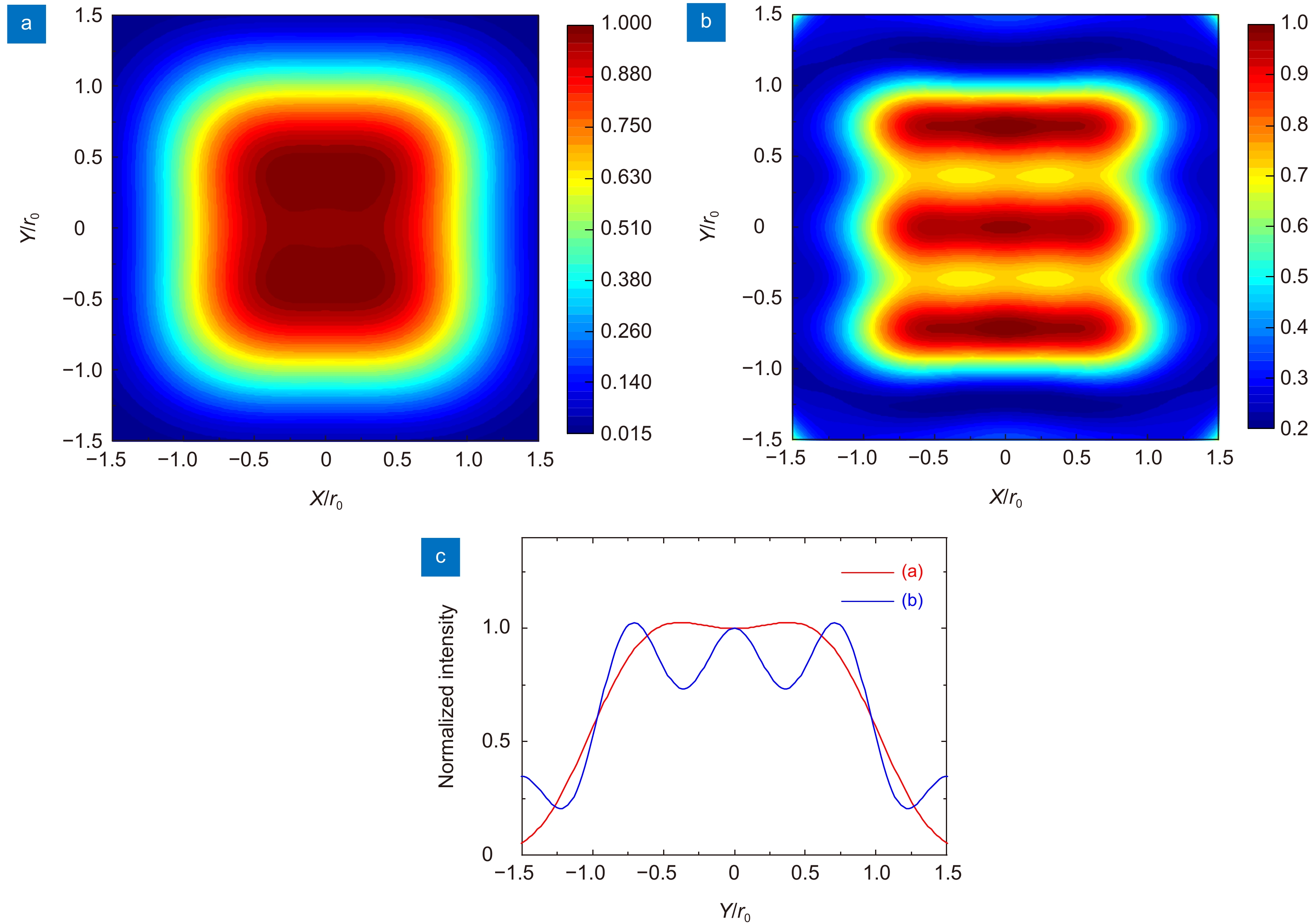
图 6 不同望远系统对三缝结构的成像结果。(a) 衍射受限望远系统对三缝结构的成像结果；(b) 超振荡望远系统对三缝结构的成像结果；(c) 红线和蓝线分别为(a)和(b)的中心竖直截面强度分布
Figure 6. Imaging results of the three-slit struct in different telescopic systems. (a) The imaging result of the three-slit struct in the diffraction limited telescopic system; (b) The imaging result of the three-slit struct in the super-oscillatory telescopic system; (c) The red and blue lines are the intensity distribution of the central vertical section of (a) and (b), respectively
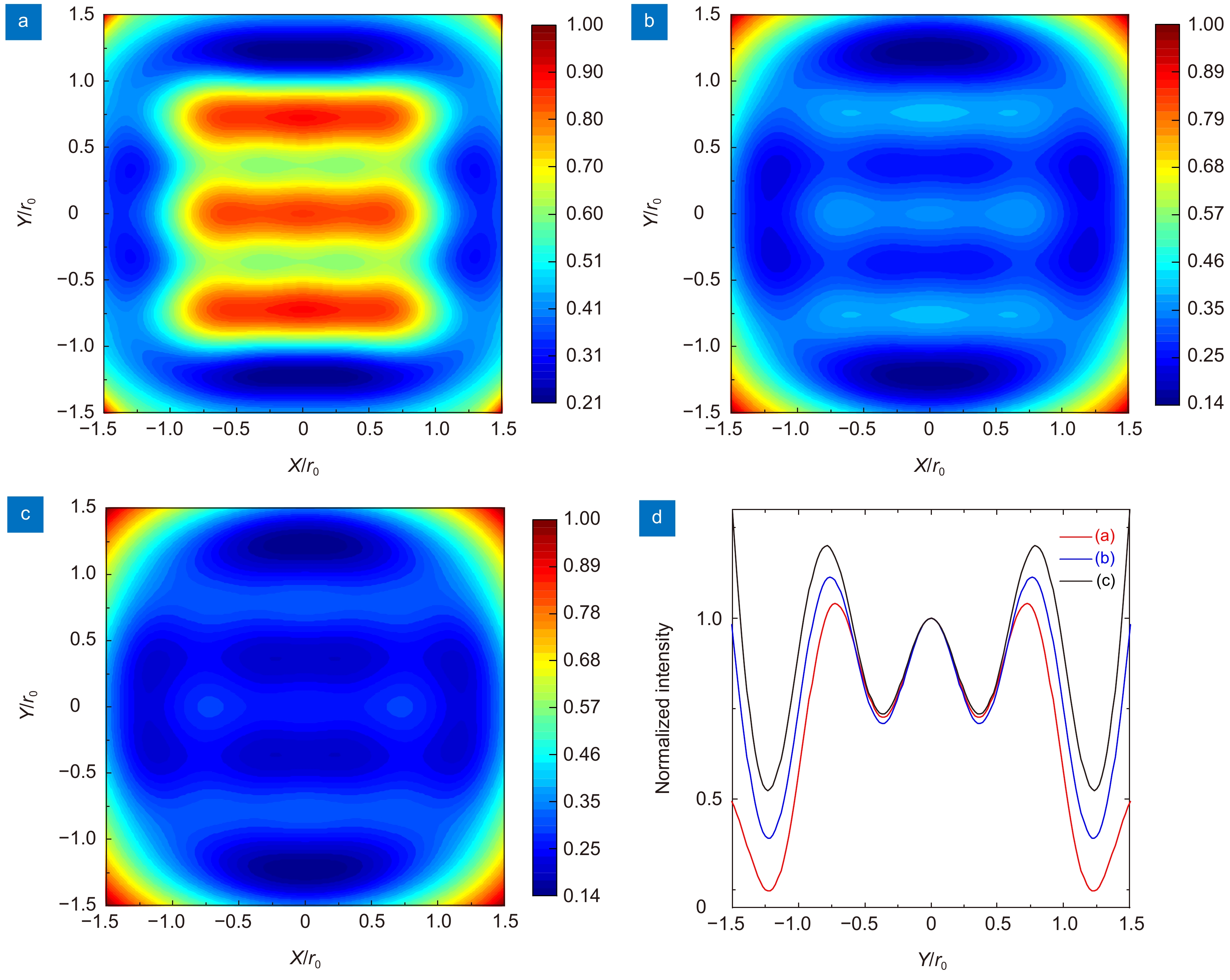
图 7 (a)-(c) 分别为RMS值为0.01λ、0.025λ、0.042λ的初级球差超振荡望远系统对三缝结构的成像结果；(d) 红、蓝、黑线分别为(a)、(b)、(c)的中心竖直截面强度分布
Figure 7. (a)-(c) Imaging results of the three-slit struct in the super-oscillatory telescopic system with primary spherical aberrations which RMS values are 0.01λ, 0.025λ and 0.042λ, respectively; (d) The red, blue and black lines are the intensity distribution of the central vertical section of (a), (b), and (c), respectively
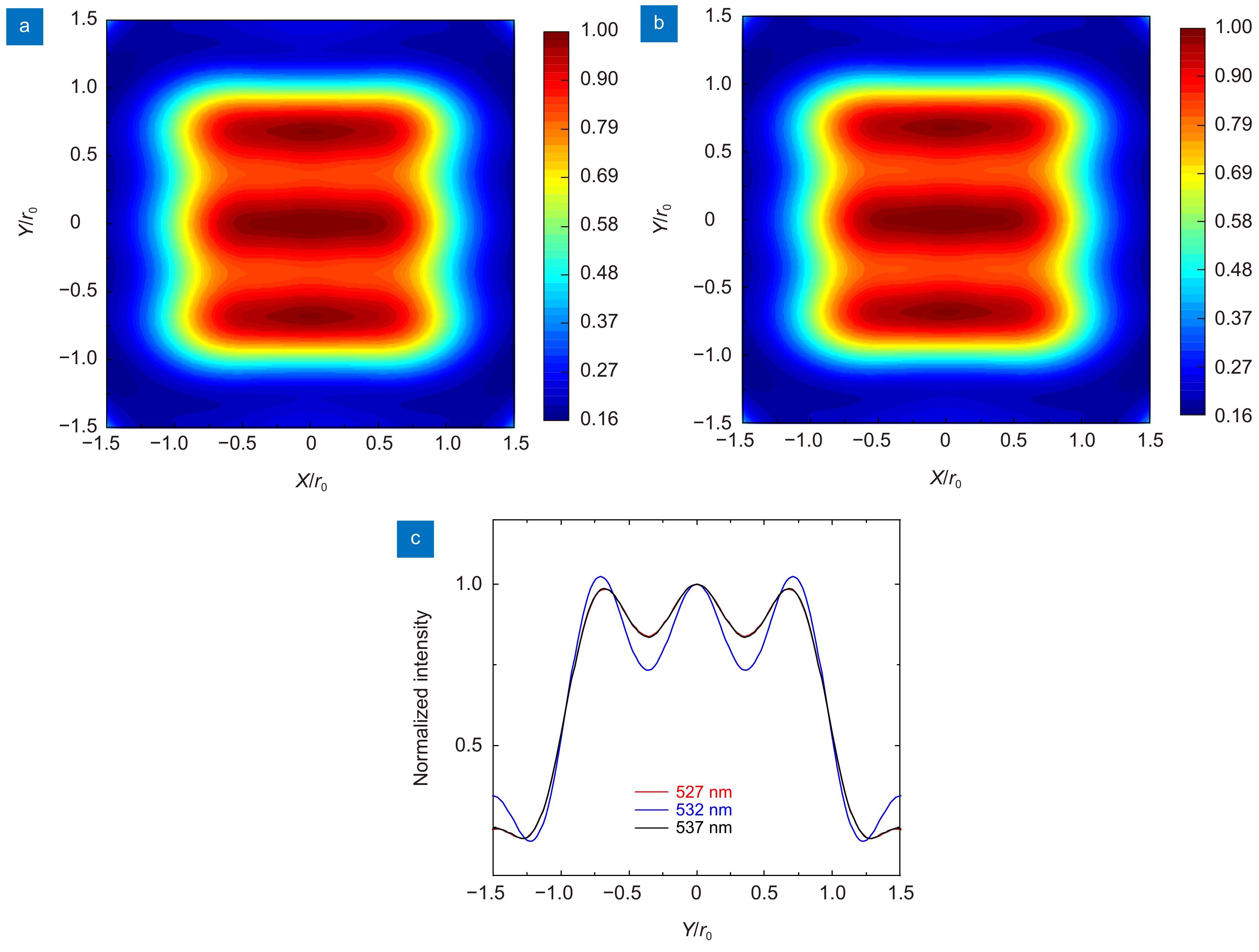
图 8 (a)-(b) 分别为527 nm、537 nm工作波长下无球差超振荡望远系统对三缝结构的成像结果；(c) 红、蓝、黑线分别为527 nm、532 nm、537 nm的中心竖直截面强度分布
Figure 8. (a)-(b) Imaging results of the three-slit struct in the super-oscillatory telescopic system without the primary aberration under working wavelength of 527 nm, 537 nm; (c) The red, blue, and black lines are the intensity distribution of the central vertical section of 527 nm, 532 nm, and 537 nm, respectively
图 9 不同初级球差，不同工作波长下，超振荡望远系统中像的中心竖直截面对比度
Figure 9. With different spherical aberrations, the contrast of the central vertical section of the image in the super-oscillatory telescopic system under different working wavelengths
-
[1] Napier-Munn T. A mathematical model to predict the resolution of double stars by amateurs and their telescopes[J]. J Double Star Obs, 2008, 4(4): 156−163.
[2] Farinas J, Simanek V, Verkman A S. Cell volume measured by total internal reflection microfluorimetry: application to water and solute transport in cells transfected with water channel homologs[J]. Biophys J, 1995, 68(4): 1613−1620. doi: 10.1016/S0006-3495(95)80335-8
[3] Klar T A, Jakobs S, Dyba M, et al. Fluorescence microscopy with diffraction resolution barrier broken by stimulated emission[J]. Proc Natl Acad Sci U S A, 2000, 97(15): 8206−8210. doi: 10.1073/pnas.97.15.8206
[4] Zheng G A, Horstmeyer R, Yang C. Wide-field, high-resolution fourier ptychographic microscopy[J]. Nat Photonics, 2013, 7(9): 739−745. doi: 10.1038/nphoton.2013.187
[5] 秦飞, 李向平, 洪明辉. 从超振荡透镜到超临界透镜: 超越衍射极限的光场调制[J]. 光电工程, 2017, 44(8): 757−771. doi: 10.3969/j.issn.1003-501X.2017.08.001
Qin F, Li X P, Hong M H. From super-osciallatory lens to super-critical lens: surpassing the diffraction limit via light field modulation[J]. Opto-Electron Eng, 2017, 44(8): 757−771. doi: 10.3969/j.issn.1003-501X.2017.08.001
[6] 周毅, 梁高峰, 温中泉, 等. 光学超分辨平面超构透镜研究进展[J]. 光电工程, 2021, 48(12): 210399. doi: 10.12086/oee.2021.210399
Zhou Y, Liang G F, Wen Z Q, et al. Recent research progress in optical super-resolution planar meta-lenses[J]. Opto-Electron Eng, 2021, 48(12): 210399. doi: 10.12086/oee.2021.210399
[7] Berry M V, Popescu S. Evolution of quantum superoscillations and optical superresolution without evanescent waves[J]. J Phys A Math Gen, 2006, 39(22): 6965−6977. doi: 10.1088/0305-4470/39/22/011
[8] Davis B J, Karl W C, Swan A K, et al. Capabilities and limitations of pupil-plane filters for superresolution and image enhancement[J]. Opt Express, 2004, 12(17): 4150−4156. doi: 10.1364/OPEX.12.004150
[9] Di Francia G T. Super-gain antennas and optical resolving power[J]. Nuovo Cim, 1952, 9(3): 426−438. doi: 10.1007/BF02903413
[10] Sheppard C J R, Campos J, Escalera J C, et al. Three-zone pupil filters[J]. Opt Commun, 2008, 281(14): 3623−3630. doi: 10.1016/j.optcom.2008.03.047
[11] Roy T, Rogers E T F, Yuan G H, et al. Point spread function of the optical needle super-oscillatory lens[J]. Appl Phys Lett, 2014, 104(23): 231109. doi: 10.1063/1.4882246
[12] Huang F M, Kao T S, Fedotov V A, et al. Nanohole array as a lens[J]. Nano Lett, 2008, 8(8): 2469−2472. doi: 10.1021/nl801476v
[13] Li M Y, Li W L, Li H Y, et al. Controllable design of super-oscillatory lenses with multiple sub-diffraction-limit foci[J]. Sci Rep, 2017, 7(1): 1335. doi: 10.1038/s41598-017-01492-y
[14] 周健文, 姚纳, 赵汗青, 等. 大气湍流下超振荡望远成像的理论研究[J]. 激光技术, 2023, 47(1): 115−120. doi: 10.7510/jgjs.issn.1001-3806.2023.01.018
Zhou J W, Yao N, Zhao H Q, et al. Theoretical study of super-oscillation telescope imaging with atmospheric turbulence[J]. Laser Technol, 2023, 47(1): 115−120. doi: 10.7510/jgjs.issn.1001-3806.2023.01.018
[15] Rogers E T F, Lindberg J, Roy T, et al. A super-oscillatory lens optical microscope for subwavelength imaging[J]. Nat Mater, 2012, 11(5): 432−435. doi: 10.1038/nmat3280
[16] Wang C T, Tang D L, Wang Y Q, et al. Super-resolution optical telescopes with local light diffraction shrinkage[J]. Sci Rep, 2015, 5: 18485. doi: 10.1038/srep18485
[17] Li W L, He P, Yuan W Z, et al. Efficiency-enhanced and sidelobe-suppressed super-oscillatory lenses for sub-diffraction-limit fluorescence imaging with ultralong working distance[J]. Nanoscale, 2020, 12(13): 7063−7071. doi: 10.1039/C9NR10697A
[18] Lu X J, Guo Y H, Pu M B, et al. Broadband achromatic metasurfaces for sub-diffraction focusing in the visible[J]. Opt Express, 2021, 29(4): 5947−5958. doi: 10.1364/OE.417036
[19] Li Z, Wang C T, Wang Y Q, et al. Super-oscillatory metasurface doublet for sub-diffraction focusing with a large incident angle[J]. Opt Express, 2021, 29(7): 9991−9999. doi: 10.1364/OE.417884
[20] Legaria S, Pacheco-Peña V, Beruete M. Super-oscillatory metalens at terahertz for enhanced focusing with reduced side lobes[J]. Photonics, 2018, 5(4): 56. doi: 10.3390/photonics5040056
[21] Li Z, Zhang T, Wang Y Q, et al. Achromatic broadband super-resolution imaging by super-oscillatory metasurface[J]. Laser Photonics Rev, 2018, 12(10): 1800064. doi: 10.1002/lpor.201800064
[22] Zhang R Z, Guo Y H, Li X Y, et al. Angular superoscillatory metalens empowers single-shot measurement of OAM modes with finer intervals[J]. Adv Opt Mater, 2023: 2300009.https://doi.org/10.1002/adom.202300009.
[23] Lu X J, Li X Y, Guo Y H, et al. Broadband high-efficiency polymerized liquid crystal metasurfaces with spin-multiplexed functionalities in the visible[J]. Photonics Res, 2022, 10(6): 1380−1393. doi: 10.1364/PRJ.452272
[24] Booth M J, Wilson T. Strategies for the compensation of specimen-induced spherical aberration in confocal microscopy of skin[J]. J Microsc, 2000, 200(1): 68−74. doi: 10.1046/j.1365-2818.2000.00735.x
[25] Booth M J, Neil M A A, Wilson T. Aberration correction for confocal imaging in refractive-index-mismatched media[J]. J Microsc, 1998, 192(2): 90−98. doi: 10.1111/j.1365-2818.1998.99999.x
[26] Gibson S F, Lanni F. Experimental test of an analytical model of aberration in an oil-immersion objective lens used in three-dimensional light microscopy[J]. J Opt Soc Am A, 1991, 8(10): 1601−1613. doi: 10.1364/JOSAA.8.001601
[27] Kam Z, Kner P, Agard D, et al. Modelling the application of adaptive optics to wide-field microscope live imaging[J]. J Microsc, 2007, 226(1): 33−42. doi: 10.1111/j.1365-2818.2007.01751.x
[28] Silvestri L, Sacconi L, Pavone F S. Correcting spherical aberrations in confocal light sheet microscopy: a theoretical study[J]. Microsc Res Tech, 2014, 77(7): 483−491. doi: 10.1002/jemt.22330
[29] Lee J U, Yu S M. Analytic design procedure of three-mirror telescope corrected for spherical aberration, coma, astigmatism, and petzval field curvature[J]. J Opt Soc Korea, 2009, 13(2): 184−192. doi: 10.3807/JOSK.2009.13.2.184
[30] González-Acuña R G, Gutiérrez-Vega J C. Analytic formulation of a refractive-reflective telescope free of spherical aberration[J]. Opt Eng, 2019, 58(8): 085105. doi: 10.1117/1.OE.58.8.085105
[31] 郁道银, 谈恒英. 工程光学[M]. 4版. 北京: 机械工业出版社, 2016:114-118; 355-356.
Yu D Y, Tan H Y. Engineering Optics[M]. 4th ed. Beijing: China Machine Press, 2016.
[32] 张润南, 蔡泽伟, 孙佳嵩, 等. 光场相干测量及其在计算成像中的应用[J]. 激光与光电子学进展, 2021, 58(18): 1811003. doi: 10.3788/LOP202158.1811003
Zhang R N, Cai Z W, Sun J S, et al. Optical-field coherence measurement and its applications in computational imaging[J]. Laser Optoelectron Prog, 2021, 58(18): 1811003. doi: 10.3788/LOP202158.1811003
[33] Hegedus Z S, Sarafis V. Superresolving filters in confocally scanned imaging systems[J]. J Opt Soc Am A, 1986, 3(11): 1892−1896. doi: 10.1364/JOSAA.3.001892
[34] Martinez-Corral M, Caballero M, Stelzer E H K, et al. Tailoring the axial shape of the point spread function using the Toraldo concept[J]. Opt Express, 2002, 10(1): 98−103. doi: 10.1364/OE.10.000098
[35] Liu H T, Yan Y B, Tan Q F, et al. Theories for the design of diffractive superresolution elements and limits of optical superresolution[J]. J Opt Soc Am A, 2002, 19(11): 2185−2193. doi: 10.1364/JOSAA.19.002185
[36] Liu H T, Yan Y B, Yi D E, et al. Theories for the design of a hybrid refractive-diffractive superresolution lens with high numerical aperture[J]. J Opt Soc Am A, 2003, 20(5): 913−924. doi: 10.1364/JOSAA.20.000913
[37] Mahajan V N. Zernike circle polynomials and optical aberrations of systems with circular pupils[J]. Appl Opt, 1994, 33(34): 8121−8124. doi: 10.1364/AO.33.008121
[38] Goodman J W. Introduction to Fourier Optics[M]. 3rd ed. New York: Roberts, 2005: 135.
[39] Xu B, Wang Z Q, He J P. Super-resolution imaging via aperture modulation and intensity extrapolation[J]. Sci Rep, 2018, 8(1): 15216. doi: 10.1038/s41598-018-33416-9
-
下载:
点击扫一扫
图(10)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
