E-mail Alert
RSS
-
摘要:
离轴反射式望远镜主要应用于空间天文观测等领域。离轴两反望远镜的成像质量对镜片的失调敏感，且在工作环境下失调后使用激光干涉仪进行校准较为困难。针对这一难题，本文提出了一种利用系统对无穷远点目标的离焦光斑图并使用Swin-Transformer网络计算次镜横向失调量的方法。通过理论计算分析，可以避免多解问题的相机离焦位置，并利用仿真探究了不同离焦量对校正精度的影响，最后搭建实验平台进行验证，训练好的网络使用失调系统的一帧离焦光斑图便可进行失调量的估计。仿真分析与实验结果均验证了该方法的有效性，可实现工作环境中失调望远镜系统的高精度和快速校正。
Abstract:Off-axis reflector telescopes are mainly used in space astronomy observation and other related fields. The image quality of off-axis two-inversion telescopes is sensitive to lens misalignment and is more difficult to calibrate using a laser interferometer after misalignment in an operating environment. To address this challenge, this paper proposes a method that uses the out-of-focus spot map of the system for infinity point targets and uses the Swin-Transformer network to calculate the amount of lateral misalignment of the secondary mirror. Theoretical calculations were used to determine the camera defocus positions that could avoid the multi-solution problem, and simulations were used to investigate the effect of different defocus amounts on calibration accuracy. The trained network uses a frame of out-of-focus spot map of the out-of-tune system to perform the estimation of the amount of out-of-tune. Both simulation analysis and experimental results verify the effectiveness of the method, which can achieve high accuracy and fast correction of out-of-tune telescope systems in the working environment.
-
Key words:
- optical imaging system /
- off-axis telescope /
- secondary mirror /
- defocused spot /
- neural Networks /
- quick adjustment
-
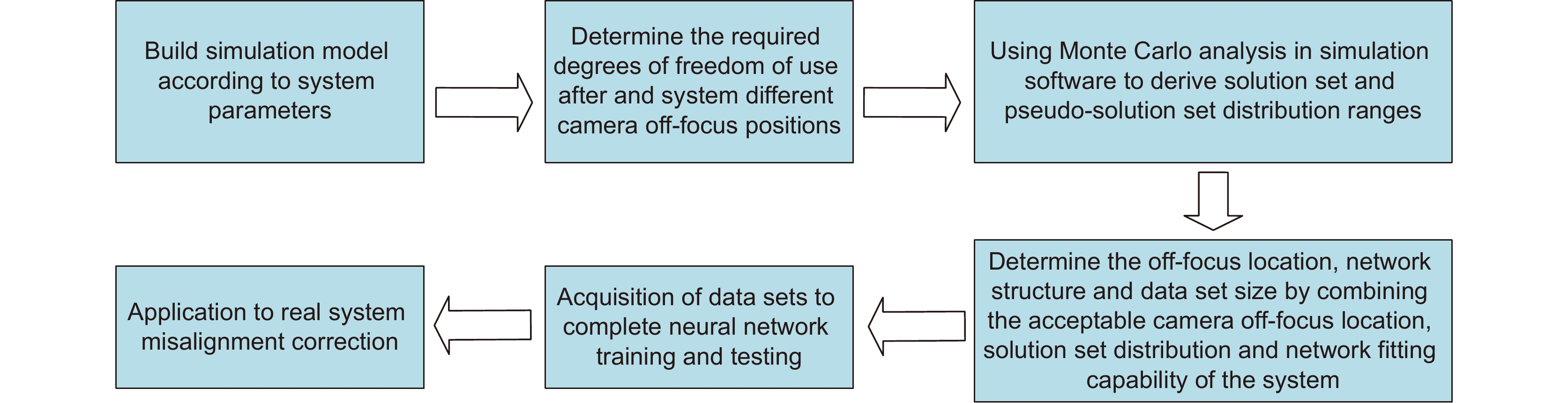
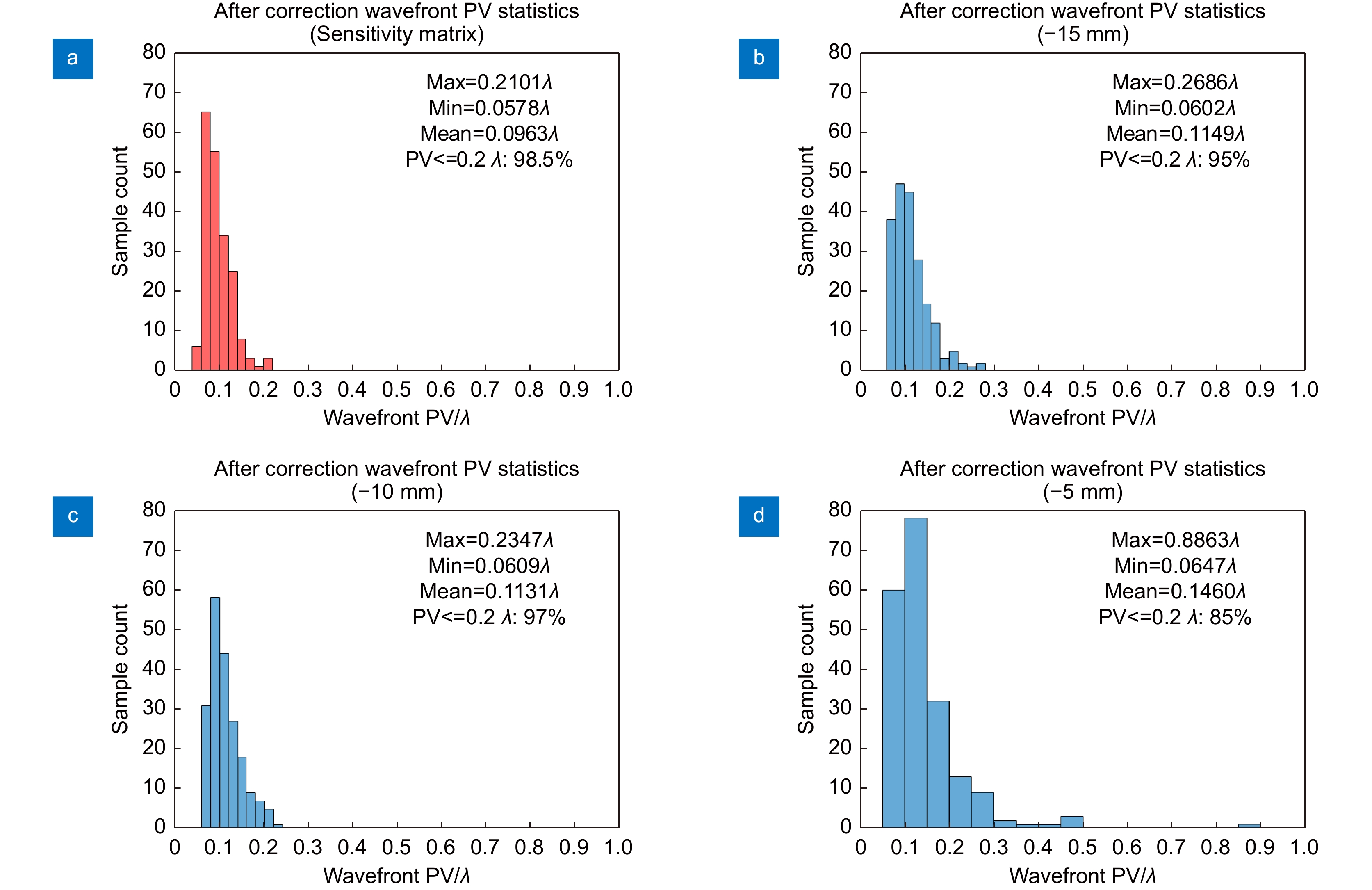
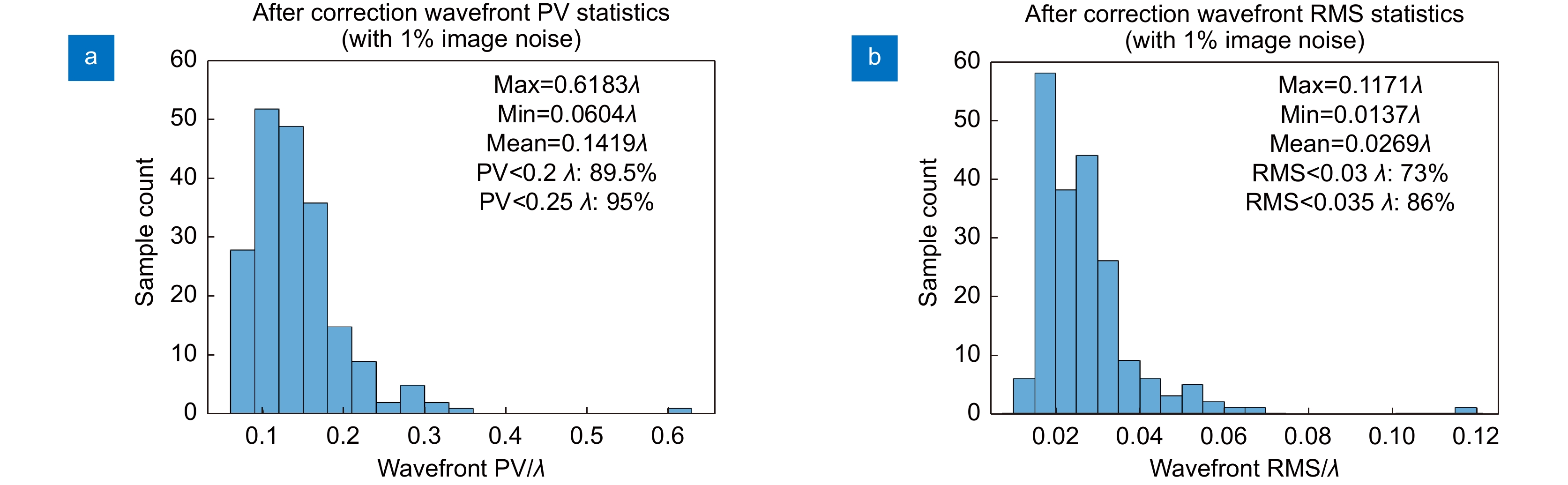
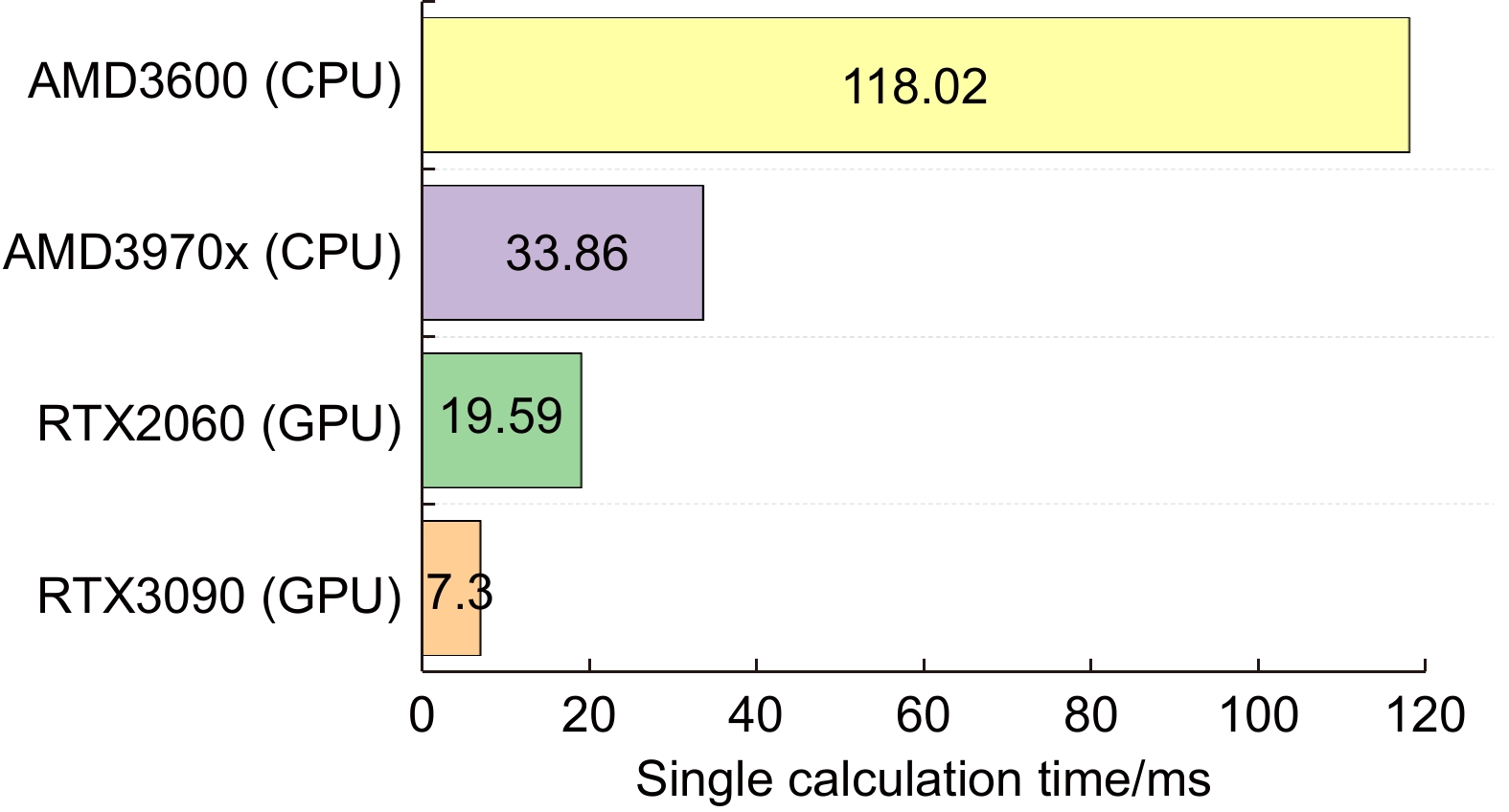
Overview: Off-axis reflector telescopes are mainly used in space astronomy observation and other fields. The imaging quality of off-axis two-reflection telescopes is sensitive to the lens misalignment. This makes the correction of out-of-tune telescope systems in the working environment hindered. To address this challenge, this paper proposes a method that uses the out-of-focus spot map of the system for infinity point targets and uses the Swin-Transformer network to calculate the amount of sub-mirror lateral misalignment. Through the derivation and analysis of the wavefront phase and point spread function formulas, it is pointed out that the use of a non-special location of the out-of-focus spot to avoid the focal spot can avoid the occurrence of multiple solutions so that the network can solve the system corresponding to the amount of misalignment from the spot morphology. In order to avoid the adverse effects of the special out-of-focus location, we observe the distribution range of the solution set and the pseudo-solution set through the Monte Carlo analysis method to determine whether the selected camera out-of-focus location is in a special position or not. We give the general implementation procedure of this method, according to which a reasonable amount of random transverse misalignment is applied to the simulation model secondary mirror in the simulation. The out-of-focus spot map is recorded to generate a dataset for network training. A test set is generated for validation, and the trained network can be used to estimate the amount of misalignment using one frame of the out-of-focus spot map of the misalignment system. The simulation shows that the out-of-focus amount is proportional to the correction accuracy within a certain out-of-focus range. Since this is an image-based method, we also tested the noise-resistance performance of the out-of-focus scheme with the highest accuracy. Finally, the predicted misalignment of the test sample set was verified by the experimental platform, and the mean prediction error of the eccentric misalignment was 0.0072 mm and the mean prediction error of the tilt misalignment was 0.0055° when compared with the real misalignment. The average computation time is less than 120 ms for a single computation when compared with the wavefront of the system before the misalignment. The simulation analysis and experimental results verify the effectiveness of the method, which can realize the misalignment telescope system in the working environment with high accuracy and fast correction.
-
-
图 4 失调样本波前统计。(a)波前PV统计；(b)波前RMS统计
Figure 4. Wavefront statistics of misaligned samples. (a) Wavefront PV statistics; (b) Wavefront RMS statistics
图 5 测试样本波前信息统计。(a)波前PV统计；(b)波前RMS统计
Figure 5. Test sample wavefront Information Statistics. (a) Wavefront PV statistics; (b) Wavefront RMS statistics
图 6 校正后波前PV统计。(a)灵敏度矩阵法；(b)离焦−15 mm；(c)离焦−10 mm；(d)离焦−5 mm
Figure 6. Wavefront PV statistics after correction. (a) Sensitivity matrix method; (b) Defocus −15 mm; (c) Defocus −10 mm; (d) Defocus −5 mm
图 7 校正后波前RMS统计。(a)灵敏度矩阵法；(b)离焦−15 mm；(c)离焦−10 mm；(d)离焦−5 mm
Figure 7. Wavefront RMS statistics after correction. (a) Sensitivity matrix method; (b) Defocus −15 mm; (c) Defocus −10 mm; (d) Defocus −5 mm
图 8 离焦−15 mm方案1%底噪下校正结果统计。(a)波前PV值统计；(b)波前RMS值统计
Figure 8. Statistics of correction results under 1% noise floor of the defocus −15 mm scheme. (a) Wavefront PV value statistics; (b) Wavefront RMS value statistics
图 11 各硬件平台单次计算平均耗时
Figure 11. The average time-consuming of a single calculation on each hardware platform
表 1 望远镜基本参数表
Table 1. Telescope basic parameters table
Parameter name Focal distance/mm F-number Caliber/mm Working wavelength/nm Parameter value 2427.12 16.3805 148 532 
下载: 导出CSV
表 2 望远镜反射面参数表
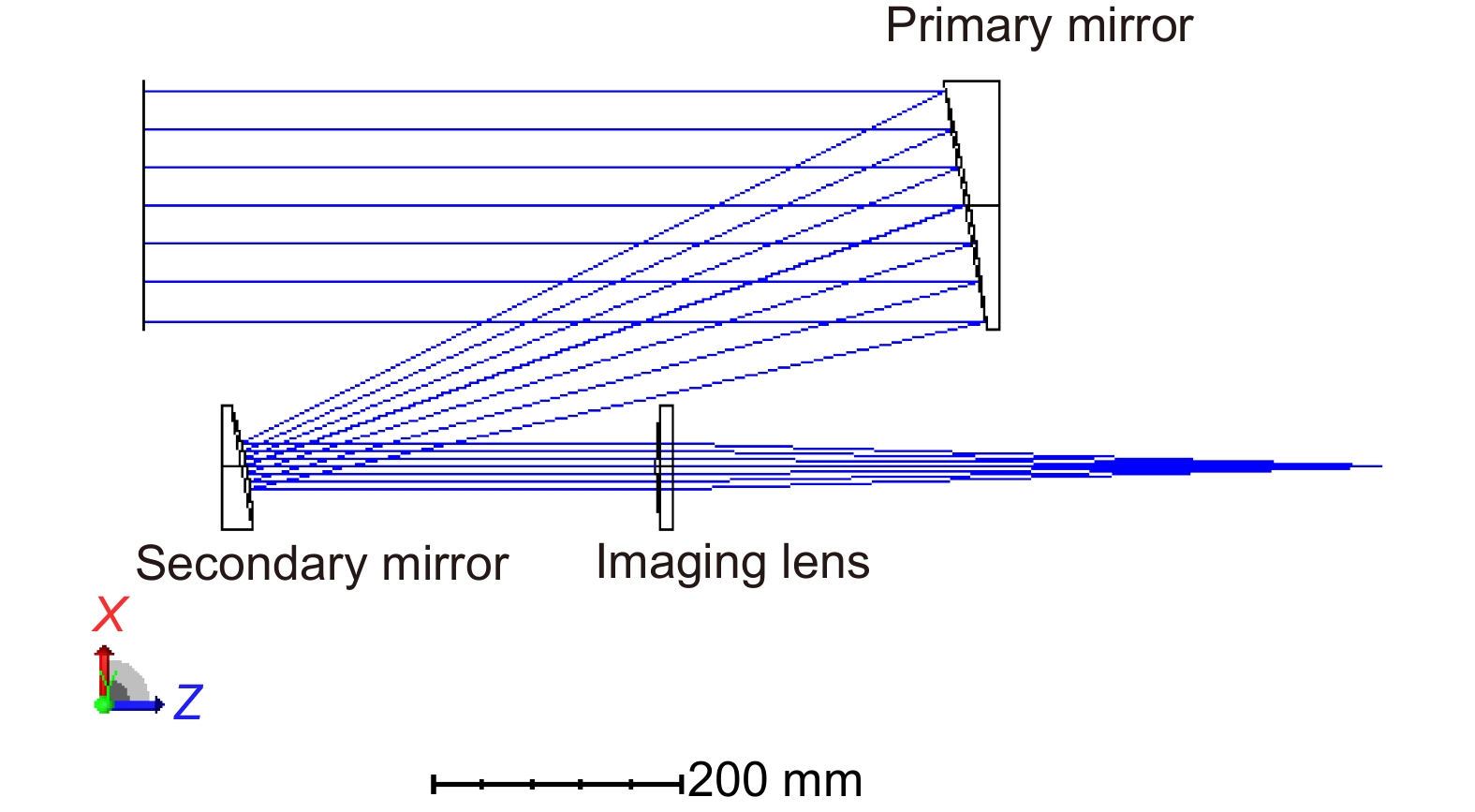
Table 2. Parameters of the telescope reflector
Surface Mechanical diameter/mm Radius of curvature/mm Interval/mm Conic factor Off-axis parameters/mm Primary mirror 148 −1200 −480 −1 210 Secondary mirror 60 −240 260 −1 42
下载: 导出CSV
表 3 离焦项系数和分布
Table 3. Coefficient and distribution of the out-of-focus term
−15 mm −10 mm −5 mm Defocus term coefficient −5.580 −3.307 −1.844 Coefficient distribution/φ [−7.0875, −3.8361] [−5.2038, −1.9909] [−3.3399, −0.1329] Coefficient distribution/φ' [4.0725, 7.3239] [1.4102,4.6231] [0.3471,3.5541]
下载: 导出CSV
表 4 网络参数汇总表
Table 4. Summary table of network parameters
Parameter name Parameter Block stacked structure [2, 2, 4, 2] Loss function MSE Loss Optimizer AdamW Initial learning rate 10E-6 Training times 2000
下载: 导出CSV
表 5 哈特曼参数表
Table 5. Hartmann parameter table
Technical parameters Value Technical parameters Value Aperture dimension 5.2 mm×7 mm Repeatability/rms <lambda/200 Number of sub-apertures dedicated
for analysis16×20 Wavefront measurement accuracy
in absolute mode/rmsMaximum between ~ lambda/100 and 6 nm Tilt dynamic range >±3°(600 lambda) Max acquisition frequency 20 Hz
下载: 导出CSV
表 6 随机失调量预测值与真值表
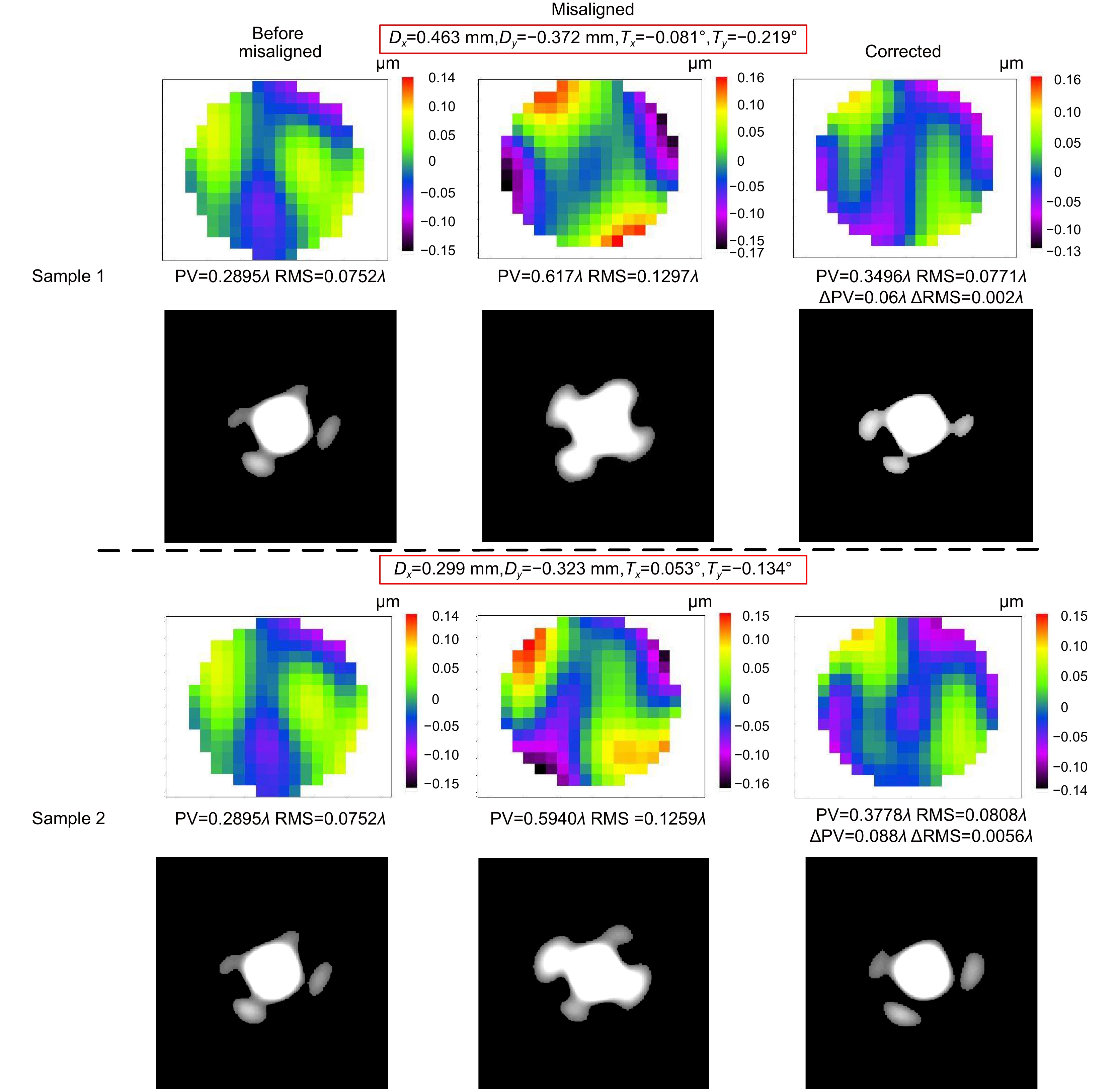
Table 6. Predicted value and truth table of random misalignment
True value / Predictive value Group 1 Group 2 Group 3 Group 4 Group 5 Dx/mm 0.499 / 0.500 0.491 / 0.496 0.088 / 0.086 0.299 / 0.313 −0.472 / −0.471 Dy/mm −0.312 / −0.325 0.101 / 0.104 0.293 / 0.287 −0.323 / −0.328 0.427 / 0.428 Tx/degree 0.063 / 0.057 0.012 / 0.012 −0.114 / −0.113 0.053 / 0.450 −0.121 / −0.120 Ty/degree 0.128 / 0.124 0.118 / 0.118 −0.067 / −0.066 −0.134 / −0.113 0.078 / 0.074
下载: 导出CSV
表 7 预测失调量残差数据统计表
Table 7. Statistical table of prediction misalignment residual data
ΔDx/mm ΔDy/mm ΔTx/degree ΔTy/degree Maximum 0.0194 0.0147 0.0170 0.0198 Minimum 2.599E-5 2.099E-5 1.100E-5 1.800E-5 Average 0.0072 0.0045 0.0037 0.0055 Standard deviation 0.01421 0.00594 0.00557 0.01028
下载: 导出CSV
-
[1] Kim S, Yang H S, Lee Y W, et al. Merit function regression method for efficient alignment control of two-mirror optical systems[J]. Opt Express, 2007, 15(8): 5059−5068. doi: 10.1364/OE.15.005059
[2] Kim D, Choi H, Brendel T, et al. Advances in optical engineering for future telescopes[J]. Opto-Electron Adv, 2021, 4(6): 210040. doi: 10.29026/oea.2021.210040
[3] Liu Z, Peng Q, Xu Y J, et al. Misalignment calculation on off-axis telescope system via fully connected neural network[J]. IEEE Photonics J, 2020, 12(4): 0600112. doi: 10.1109/jphot.2020.3005910
[4] Ju G H, Ma H C, Yan C X. Aberration fields of off-axis astronomical telescopes induced by rotational misalignments[J]. Opt Express, 2018, 26(19): 24816−24834. doi: 10.1364/OE.26.024816
[5] Zhang X B, Zhang D, Xu S Y, et al. Active optical alignment of off-axis telescopes based on nodal aberration theory[J]. Opt Express, 2016, 24(23): 26392−26413. doi: 10.1364/OE.24.026392
[6] Lee H, Dalton G B, Tosh I A J, et al. Computer-guided alignment I: phase and amplitude modulation of alignment-influenced optical wavefront[J]. Opt Express, 2007, 15(6): 3127−3139. doi: 10.1364/OE.15.003127
[7] Guerra-Ramos D, Díaz-García L, Trujillo-Sevilla J, et al. Piston alignment of segmented optical mirrors via convolutional neural networks[J]. Opt Lett, 2018, 43(17): 4264−4267. doi: 10.1364/OL.43.004264
[8] Oteo E, Arasa J. New strategy for misalignment calculation in optical systems using artificial neural networks[J]. Opt Eng, 2013, 52(7): 074105. doi: 10.1117/1.OE.52.7.074105
[9] 戴勋义, 谭毅, 任戈, 等. 扫描哈特曼方法的像质检测性能分析[J]. 光学学报, 2020, 40(7): 0712002. doi: 10.3788/AOS202040.0712002
Dai X Y, Tan Y, Ren G, et al. Analysis of image quality detection performance of scanning Hartmann technology[J]. Acta Opt Sin, 2020, 40(7): 0712002. doi: 10.3788/AOS202040.0712002
[10] 毕津慈, 高志山, 朱丹, 等. 基于粒子群优化算法的光学相干层析像差校正方法[J]. 光学学报, 2020, 40(10): 1011002. doi: 10.3788/AOS202040.1011002
Bi J C, Gao Z S, Zhu D, et al. An optical coherence tomographic aberration correction method based on the particle swarm optimization algorithm[J]. Acta Opt Sin, 2020, 40(10): 1011002. doi: 10.3788/AOS202040.1011002
[11] 周明尧, 侯俊峰, 王东光, 等. 天文望远镜无偏消旋镜装调方案设计及验证[J]. 中国激光, 2020, 47(6): 0604005. doi: 10.3788/CJL202047.0604005
Zhou M Y, Hou J F, Wang D G, et al. Design and verification of depolarized derotator alignment scheme in astronomical telescope[J]. Chin J Lasers, 2020, 47(6): 0604005. doi: 10.3788/CJL202047.0604005
[12] 王钰, 张新, 王灵杰, 等. 基于人工神经网络方法的自由曲面光学系统装调[J]. 光学学报, 2013, 33(12): 1211001. doi: 10.3788/AOS201333.1211001
Wang Y, Zhang X, Wang L J, et al. Freeform optical system alignment based on artificial neural networks[J]. Acta Opt Sin, 2013, 33(12): 1211001. doi: 10.3788/AOS201333.1211001
[13] Ma X F, Xie Z L, Ma H T, et al. Piston sensing of sparse aperture systems with a single broadband image via deep learning[J]. Opt Express, 2019, 27(11): 16058−16070. doi: 10.1364/OE.27.016058
[14] Xu Y J, He D, Wang Q, et al. An improved method of measuring wavefront aberration based on image with machine learning in free space optical communication[J]. Sensors, 2019, 19(17): 3665. doi: 10.3390/s19173665
[15] 李志俊, 毛耀, 亓波, 等. 量子光通信中位置修正单检测控制方法[J]. 光电工程, 2022, 49(3): 210311. doi: 10.12086/oee.2022.210311
Li Z J, Mao Y, Qi B, et al. Research on control technology of single detection based on position correction in quantum optical communication[J]. Opto-Electron Eng, 2022, 49(3): 210311. doi: 10.12086/oee.2022.210311
[16] 张良总, 杨涛, 吴云, 等. 基于图像测量的Stewart平台双阶控制技术[J]. 光电工程, 2022, 49(8): 220019. doi: 10.12086/oee.2022.220019
Zhang L Z, Yang T, Wu Y, et al. Image measurement-based two-stage control of Stewart platform[J]. Opto-Electron Eng, 2022, 49(8): 220019. doi: 10.12086/oee.2022.220019
[17] 夏文强, 何秋农, 段倩文, 等. 基于传感器优化与鲁棒预测的等效加速度前馈[J]. 光电工程, 2021, 48(11): 210153. doi: 10.12086/oee.2021.210153
Xia W Q, He Q N, Duan Q W, et al. Equivalent acceleration feedforward based on sensor optimization and robust prediction[J]. Opto-Electron Eng, 2021, 48(11): 210153. doi: 10.12086/oee.2021.210153
[18] 邹雨彤. 光学成像系统中的自动检焦技术研究[D]. 成都: 中国科学院大学(中国科学院光电技术研究所), 2021.
Zou Y T. Research on auto focus technology in optical imaging system[D]. Chengdu: The Institute of Optics and Electronics, The Chinese Academy of Sciences, 2021.
[19] 马晓雨. 基于光学检测与图像处理相结合的调焦技术研究[D]. 西安: 中国科学院大学(中国科学院西安光学精密机械研究所), 2020.
Ma X Y. The research on focusing technology based on the combination of optical detecting and image processing[D]. Xi’an: Xi'an Institute of Optics & Precision Mechanics, Chinese Academy of Sciences, 2020.
[20] 李启辉, 丁亚林, 修吉宏, 等. 基于图像处理的自准直检焦方法[J]. 激光与光电子学进展, 2020, 57(2): 021104. doi: 10.3788/LOP57.021104
Li Q H, Ding Y L, Xiu J H, et al. Self-collimation inspection and focusing method based on image processing[J]. Laser Optoelectron Prog, 2020, 57(2): 021104. doi: 10.3788/LOP57.021104
[21] 刘柱. 离轴望远镜失调误差检测技术研究[D]. 成都: 中国科学院大学(中国科学院光电技术研究所), 2021.
Liu Z. Study on off-axis telescope misalignment detection technology[D]. Chengdu: The Institute of Optics and Electronics, The Chinese Academy of Sciences, 2021.
[22] 李蕾. 基于Zernike矢量多项式的离轴反射系统装调技术研究[D]. 长春: 中国科学院大学(中国科学院长春光学精密机械与物理研究所), 2020.
Li L. Alignment technique for off-axis reflective systems based on Zernike vector polynomials[D]. Changchun: Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, 2020.
[23] 周文, 陈秀峰, 杨冬晓. 光子学基础[M]. 杭州: 浙江大学出版社, 2000.
Zhou W, Chen X F, Yang D X. Fundamentals of Photonics[M]. Hangzhou: Zhejiang University Press, 2000.
[24] 周亮, 刘朝晖, 单秋莎, 等. 大景深成像系统中目标离焦量的测定[J]. 光子学报, 2018, 47(10): 1011003. doi: 10.3788/gzxb20184710.1011003
Zhou L, Liu Z H, Shan Q S, et al. Measurement of the object defocus with extended depth-of-field imaging system[J]. Acta Photon Sin, 2018, 47(10): 1011003. doi: 10.3788/gzxb20184710.1011003
[25] Liu Z, Lin Y T, Cao Y, et al. Swin transformer: hierarchical vision transformer using shifted windows[C]//Proceedings of 2021 IEEE/CVF International Conference on Computer Vision, Montreal, 2021: 9992–10002. https://doi.org/10.1109/ICCV48922.2021.00986.
-
点击扫一扫
图(12)
表(7)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
