E-mail Alert
RSS
-
摘要:
本文提出了采用连续镜面变形反射镜的本征模法构建了完备正交基，通过需要调控的涡旋光场信息，来求解变形反射镜各个驱动器的电压。调控生成了拓扑荷数绝对值在5以内的整数阶、分数阶、多分数阶和叠加态的螺旋波前，实现了对涡旋光束的动态调控。生成结果与理想螺旋波前结果基本一致。显示了连续镜面变形反射镜拟合螺旋波前的能力，得到了较好的结果。该方法在高功率涡旋激光的动态调控上具有很好的应用前景。
Abstract:A complete orthogonal basis was constructed by using the eigen-mode method of continuous surface deformation mirror, and the voltage of each driver of the deformation mirror can be obtained according to the spiral wavefront information which needs to be manipulated. The spiral wavefront of integral order, fractional order, multi-fractional order, and superposition state with the absolute value of topological charge less than 5 was generated, and the dynamic manipulation of the vortex beam was realized. The results obtained were the same as those obtained by the ideal spiral wavefront. The ability of the continuous surface deformation mirror to fit the spiral wavefront was demonstrated and good results were obtained. This method has a good application prospect in the dynamic manipulation of high-power vortex laser.
-
Key words:
- voretex beam /
- deformation mirror /
- eigen-mode /
- mode purity /
- dynamic manipulation
-
Overview: In recent years, vortex beams have become the focus of research, and their orbital angular momentum makes them have many important applications, like optical communication, particle manipulation, and optical measurement. At the same time, researchers are paying attention to more abundant generation methods. In previous studies, vortex beam generation methods are usually divided into two categories. The first category is the outcavity, such as spiral phase plate method, spatial light modulator method, mode conversion method, metasurface method, and corner array method, and the second category is the incavity, such as point-loss method, off-axis pumping method, and spatial light modulator method. However, these methods can not tolerate high power laser output and adjust topological charges flexibly. Therefore, how to generate a vortex beam that can tolerate high power laser output and adjust the topological charges flexibly is an important problem to be solved. Continuous surface deformation mirror is a key component of adaptive optical system. In the study of wavefront fitting for continuous surface deformation mirrors, there are usually two kinds of methods. The first type is model-free method, such as genetic algorithm, simulated annealing algorithm, stochastic parallel gradient descent (SPGD) algorithm, etc. These methods generally require many iterations and slow convergence, and it is difficult to change the topological charge flexibly. The second type is pattern method, such as Zernike mode method, Lukosz mode method, and enginmode method. This method first defines a set of complete orthogonal modes, calculates the mode coefficients, and completes the fitting of the target wavefront by linear superposition of each mode. Zernike mode is orthogonal in the circular domain, Lukosz mode is orthogonal in the circular domain derivative. However, usually the configuretion of deformation mirror is not circular domain. For example, the deformation mirror driver used in this paper is arranged in circular domain. In this case, the orthogonal basis needs to be rebuilt to use these two methods. The eigenmode of the deformed mirror is directly and precisely derived from the influence function of the deformed mirror drivers, so it can not only avoid the influence of fitting error, improve the fitting accuracy, but also adapt to the different configuration of the deformed mirror. Combined with the eigenmode method, continuous surface deformation mirror can fit all kinds of vortex beams with high precision and fast fitting speed, and can be applied to all kinds of deformation mirrors with different configurations. In this paper, the eigenmode method of continuous surface deformation mirror is used to simulate and analyze the fitting of the spiral wavefront of integer order with topological charge is −5 to 5, fractional order, multi-fractional order, and superposition state with the absolute value of topological charge less than 5. Various vortex light fields are generated by dynamic manipulation. The results show that the continuous surface deformation mirror will have a good application prospect in the field of high-power vortex field manipulation.
-
-
图 1 连续镜面变形反射镜生成涡旋光束的示意图
Figure 1. Schematic diagram of the vortex beam generated by continuous mirror deformation mirror
图 2 使用变形镜生成涡旋光束的示意图。L1、L2、L3：凸透镜；T：孔径光阑；DM：变形镜；f：焦距
Figure 2. Schematic diagram of using DM to generate vortex beams.L1, L2, L3: convex lens; T: aperture; DM: deformation mirror; f: focal length
图 3 整数阶螺旋波前的拟合。(a)~(e) 拓扑荷数为l=1~5的整数阶目标波前; (f)~(j) 拓扑荷数为l=1~5的整数阶拟合波前
Figure 3. Fitting of the integer order spiral wavefront. (a)~(e) Target wavefront with the integer order l =1~5; (f)~(j) Fitting wavefront of the integer order l=1~5
图 4 拓扑荷数为2的涡旋光束的拟合。(a) u2处未滤波的光强; (b) u4处经过滤波的光强; (c) u2处未滤波的相位; (d) u4处经过滤波的相位
Figure 4. Fitting of integer order vortex beams with topological charge is 2. (a) Unfiltered intensity at u2; (b) Filtered intensity at u4; (c) Unfiltered phase at u2; (d) Filtered phase at u4
图 5 整数阶拟合波前在经过滤波处理后的光场及相位。(a)~(d) 拓扑荷数为1、3、4、5的光强；(e)~(h) 拓扑荷数为1、3、4、5的相位
Figure 5. The light field and phase of the integer order vortex beam after focusing and filtering. (a)~(d) Intensity with topological charges l=1, 3, 4, and 5; (e)~(h) Phase with topological charges l=1, 3, 4, and 5
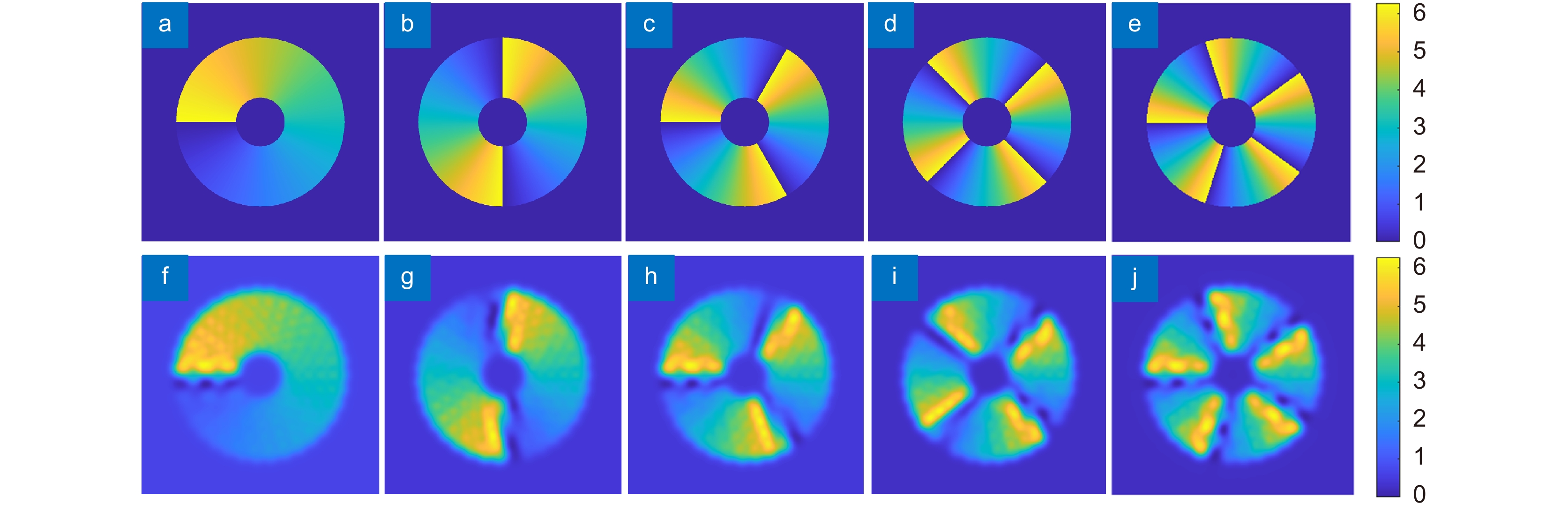
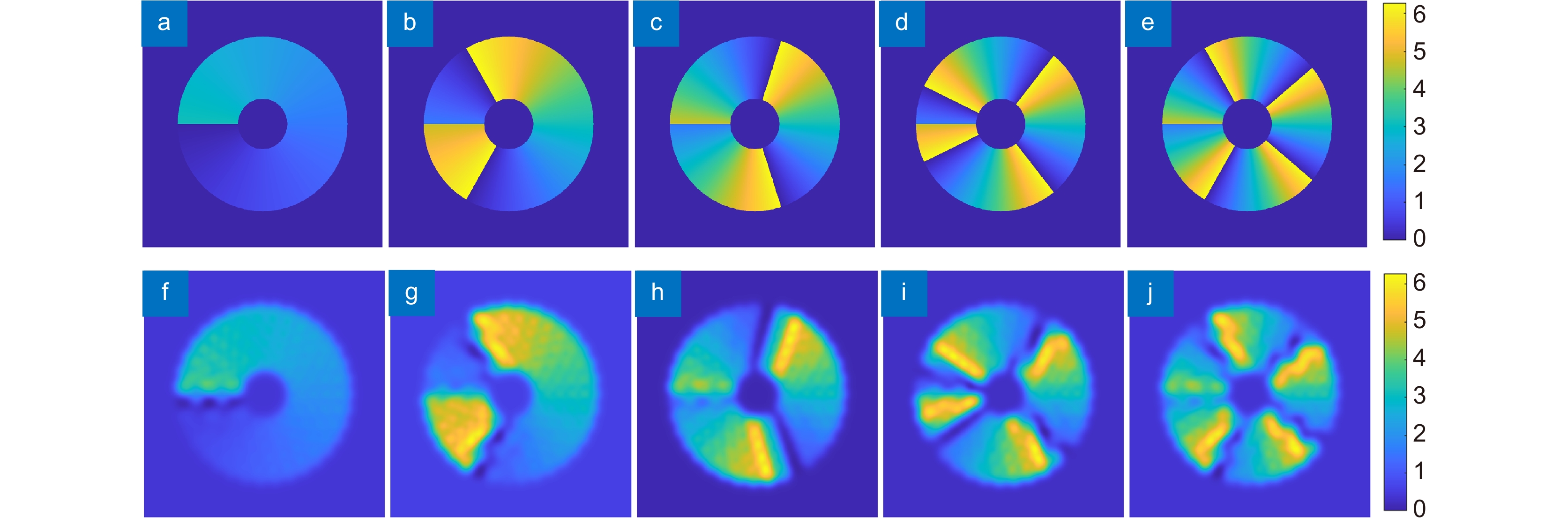
图 6 分数阶螺旋波前的拟合。(a)~(e) 拓扑荷数为l=0.5、1.5、2.5、3.5、4.5的目标波前；(f)~(j) 拓扑荷数为l=0.5、1.5、2.5、3.5、4.5的拟合波前
Figure 6. Fitting of the fractional order spiral wavefront. (a)~(e) Target wavefront with topological charges l=0.5, 1.5, 2.5, 3.5, and 4.5; (f)~(j) Fitting wavefront with topological charges l=0.5, 1.5, 2.5, 3.5, and 4.5
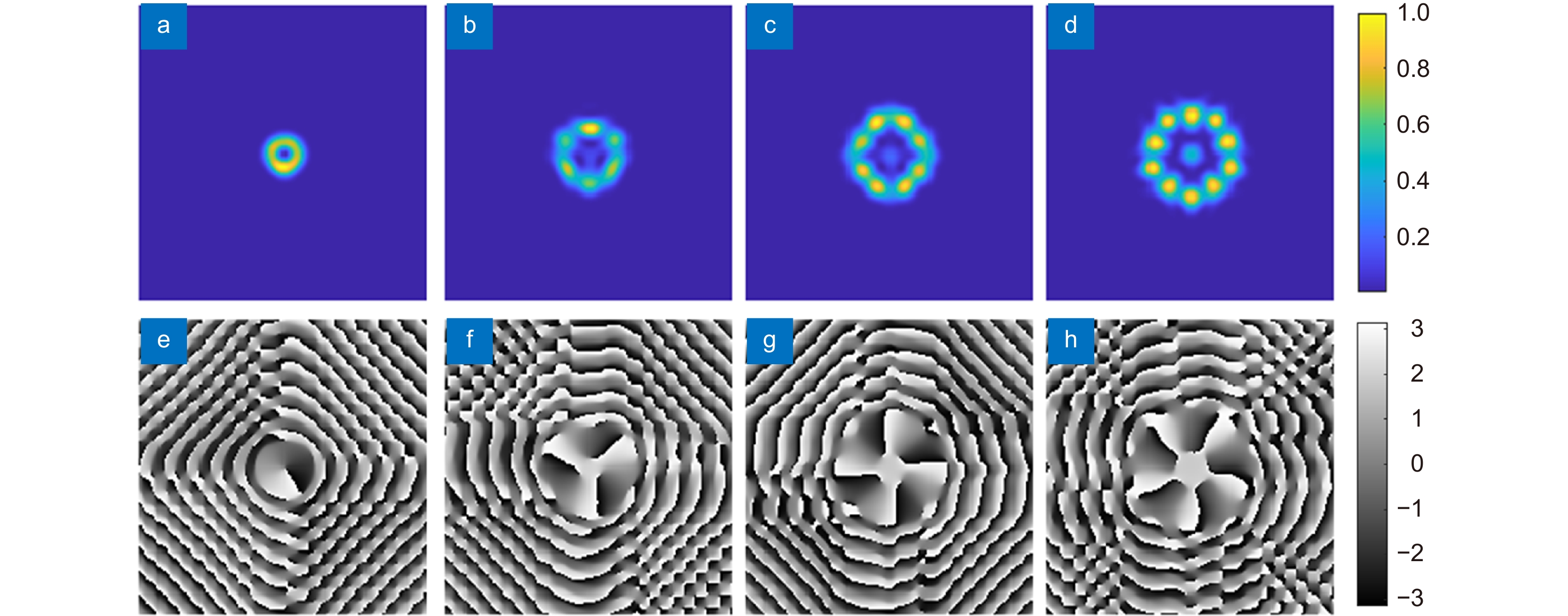
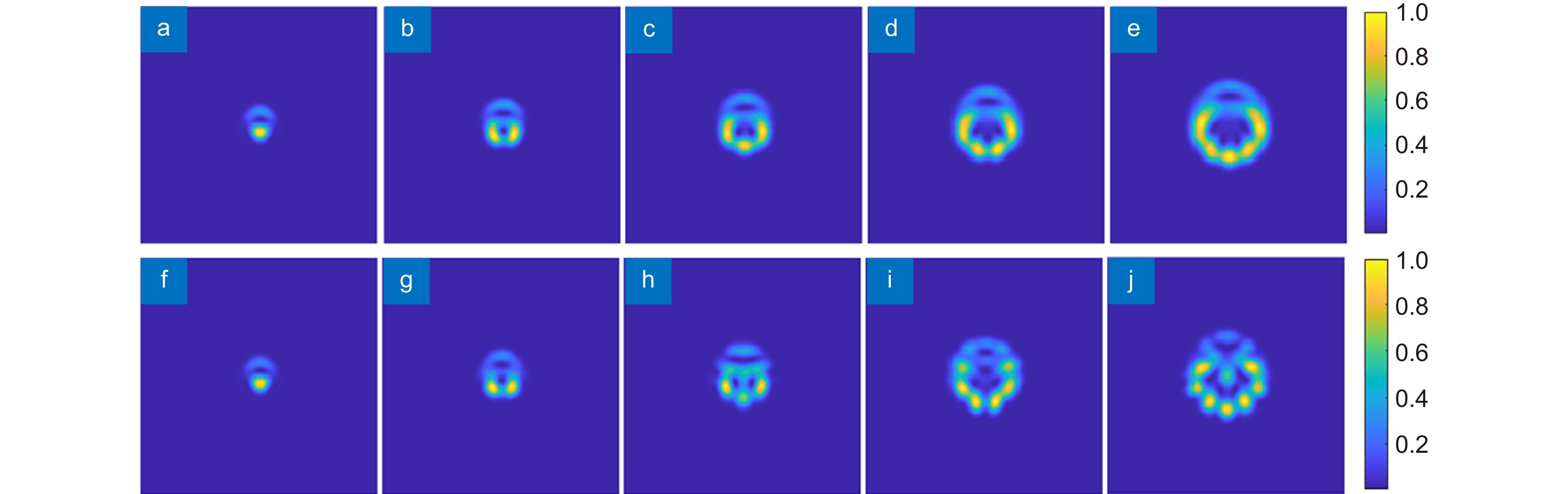
图 7 分数阶涡旋光束的滤波结果。(a)~(e) 拓扑荷数为l=0.5、1.5、2.5、3.5、4.5的目标波前在u4处的光强; (f)~(j) 拓扑荷数为l=0.5、1.5、2.5、3.5、4.5的拟合波前在u4处的光强
Figure 7. Filtering results of the fractional order vortex beam. (a)~(e) Intensity of target wavefront with topological charges l=0.5, 1.5, 2.5, 3.5, and 4.5 at u4; (f)~(j) Intensity of fitting wavefront with topological charges l=0.5, 1.5, 2.5, 3.5, and 4.5 at u4
图 8 分数阶涡旋光束的滤波结果。(a)~(e) 拓扑荷数为l=0.5、1.5、2.5、3.5、4.5的目标波前在u4处的相位; (f)~(j) 拓扑荷数为l=0.5、1.5、2.5、3.5、4.5的拟合波前在u4处的相位
Figure 8. Filtering results of the fractional order vortex beam. (a)~(e) Phase of target wavefront with topological charges l=0.5, 1.5, 2.5, 3.5, and 4.5 at u4; (f)~(j) Phase of fitting wavefront with topological charges l=0.5, 1.5, 2.5, 3.5, and 4.5 at u4
图 9 多分数阶螺旋波前的拟合。(a), (b) 目标波前；(c), (d) 拟合波前
Figure 9. Fitting of multi-fractional spiral wavefront. (a), (b) Target wavefront; (c), (d) Fitting wavefront
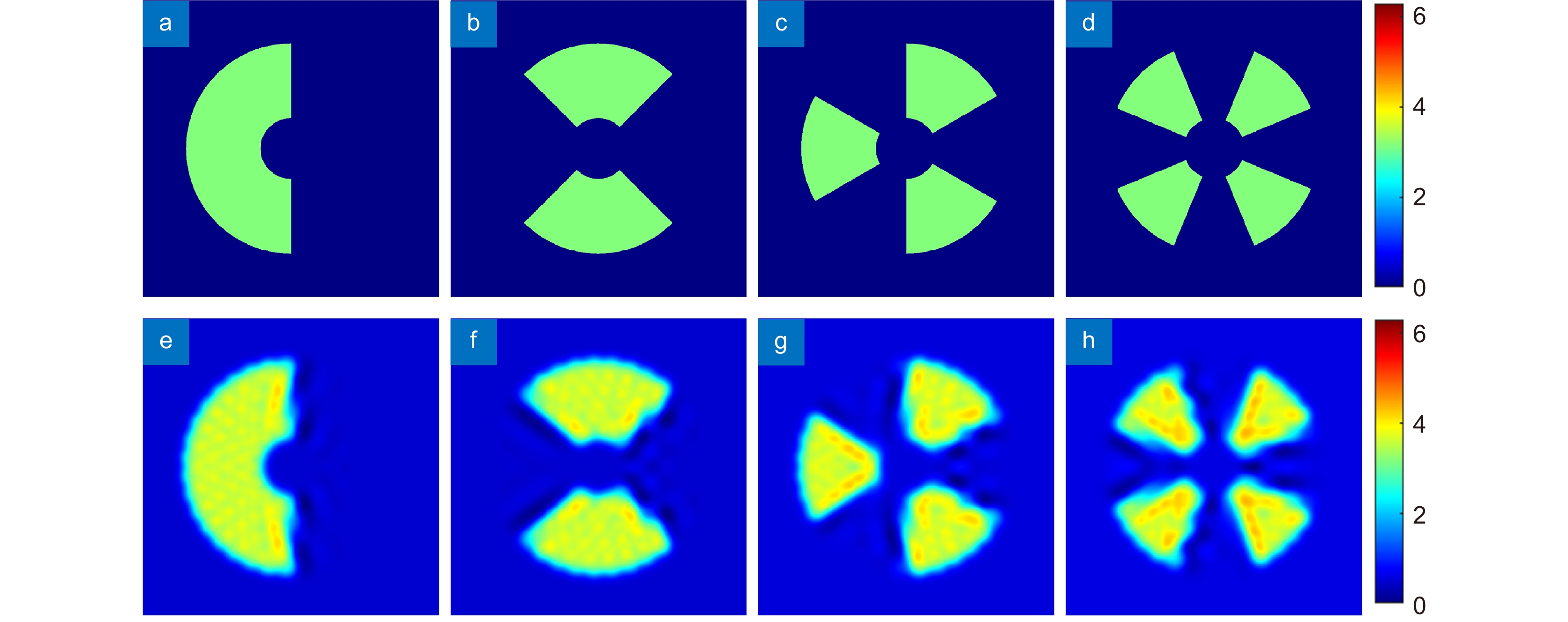
图 10 多分数阶目标波前及拟合波前在滤波处理后的光场及相位。(a), (b) 多分数阶目标波前在u4处的光强; (c), (d) 多分数阶拟合波前在u4处的光强; (e), (f) 多分数阶目标波前在u4处的相位; (g), (h) 多分数阶拟合波前在u4处的相位
Figure 10. The light field and phase of the multi-fractional order target wavefront and the fitting wavefront after filtering. (a), (b) Intensity of multi-fractional order target wavefront at u4; (c), (d) Intensity of multi-fractional order fitting wavefront at u4; (e), (f) Phase of multi-fractional order target wavefront at u4; (g), (h) Phase of multi-fractional order fitting wavefront at u4
图 11 叠加态目标波前及拟合波前。(a)~(d) 拓扑荷数分别为l=±1、±2、±3、±4的目标波前; (e)~(h) 拓扑荷数分别为l=±1、±2、±3、±4的拟合波前
Figure 11. Superposition target wavefront and fitting wavefront. (a)~(d) Target wavefront with topological charges l=±1, ±2, ±3, and ±4; (e)~(h) Fitting wavefront with topological charges l=±1, ±2, ±3, and ±4
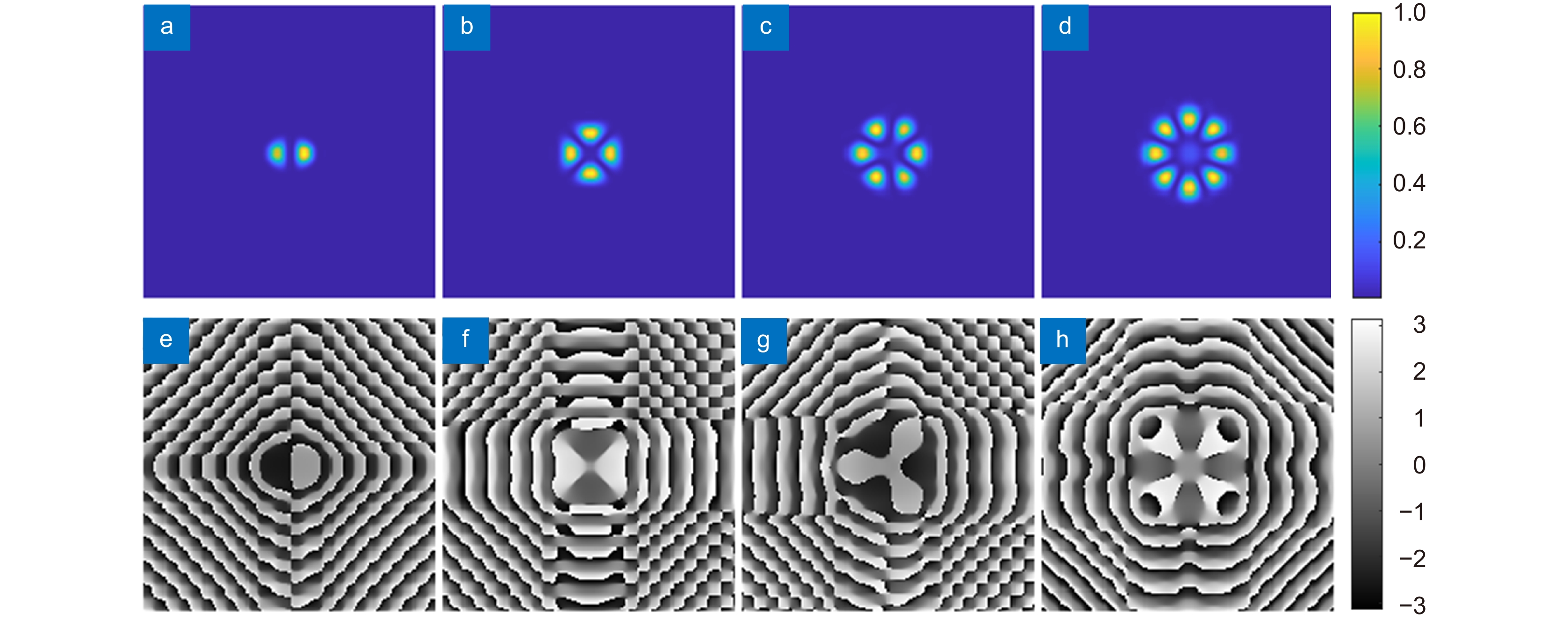
图 12 叠加态拟合波前在滤波处理后的光场及相位。(a)~(d) 拓扑荷数分别为l=±1、±2、±3、±4的拟合波前在u4处的光强; (e)~(h) 拓扑荷数分别为l=±1、±2、±3、±4的拟合波前在u4处的相位
Figure 12. The light field and phase of the superposition fitting wavefront after filtering. (a)~(d) Intensity of fitting wavefront at with topological chrages l=±1，±2，±3, and ±4 at u4; (e)~(h) Phase of fitting wavefront at with topological chrages l=±1，±2，±3, and ±4 at u4
图 13 叠加态拟合波前在滤波处理后的模式纯度。(a) l=±1；(b) l=±2；(c) l=±3；(d) l=±4
Figure 13. The mode purity of the superposition fitting wavefront after filtering. (a) l=±1; (b) l=±2; (c) l=±3; (d) l=±4
图 14 整数阶涡旋光束的动态调控。(a1)~(a6) 拓扑荷数为2的光强；(b1)~(b6) 拓扑荷数为2的螺旋相位；(c1)~(c6) 拓扑荷数为3的光强；(d1)~(d6) 拓扑荷数为3的螺旋相位
Figure 14. Dynamic manipulation of integer order vortex beams. (a1)~(a6) Intensity with topological charge l=2; (b1)~(b6) Spiral phase with topological charge l= 2; (c1)~(c6) Intensity with topological charge l=3; (d1)~(d6) Spiral phase with topological charge l= 3
-
[1] Shen Y J, Wang X J, Xie Z W, et al. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities[J]. Light Sci Appl, 2019, 8: 90. doi: 10.1038/s41377-019-0194-2
[2] Gahagan K T, Swartzlander G A. Optical vortex trapping of particles[J]. Opt Lett, 1996, 21(11): 827−829. doi: 10.1364/OL.21.000827
[3] He H, Friese M E J, Heckenberg N R, et al. Direct observation of transfer of angular momentum to absorptive particles from a laser beam with a phase singularity[J]. Phys Rev Lett, 1995, 75(5): 826−829. doi: 10.1103/PhysRevLett.75.826
[4] Figliozzi P, Sule N, Yan Z J, et al. Driven optical matter: dynamics of electrodynamically coupled nanoparticles in an optical ring vortex[J]. Phys Rev E, 2017, 95(2): 022604. doi: 10.1103/PhysRevE.95.022604
[5] Zhang Y X, Liu X F, Lin H, et al. Ultrafast multi-target control of tightly focused light fields[J]. Opto-Electron Adv, 2022, 5(3): 210026. doi: 10.29026/oea.2022.210026
[6] Bozinovic N, Yue Y, Ren Y X, et al. Terabit-scale orbital angular momentum mode division multiplexing in fibers[J]. Science, 2013, 340(6140): 1545−1548. doi: 10.1126/science.1237861
[7] Huang H, Yue Y, Ahmed N, et al. Systems and techniques for orbital angular momentum based reconfigurable switching: 2015/349910 A1[P]. 2015-12-03.
[8] Du J, Li S H, Zhao Y F, et al. Demonstration of M-ary encoding/decoding using visible-light Bessel beams carrying orbital angular momentum (OAM) for free-space obstruction-free optical communications[C]//Proceedings of 2015 Optical Fiber Communications Conference and Exhibition (OFC), Los Angeles, CA, 2015. doi: 10.1364/OFC.2015.M2F.4.
[9] 柯熙政, 郭新龙. 用光束轨道角动量实现相位信息编码[J]. 量子电子学报, 2015, 32(1): 69−76. doi: 10.3969/j.issn.1007-5461.2015.01.010
Ke X Z, Guo X L. Realization of optical phase information encode by using orbital angular momentum of light beam[J]. Chin J Quantum Electron, 2015, 32(1): 69−76. doi: 10.3969/j.issn.1007-5461.2015.01.010
[10] Li S H, Xu Z D, Liu J, et al. Experimental demonstration of free-space optical communications using orbital angular momentum (OAM) array encoding/decoding[C]//Proceedings of 2015 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, 2015. doi: 10.1364/CLEO_AT.2015.JTh2A.67.
[11] 周红平, 潘珍珍, 郭凯, 等. OAM光通信系统能量利用效率研究[J]. 电子学报, 2021, 49(10): 1881−1892. doi: 10.12263/DZXB.20210231
Zhou H P, Pan Z Z, Guo K, et al. Research on the energy-utilization efficiency of OAM based optical communication systems[J]. Acta Electron Sin, 2021, 49(10): 1881−1892. doi: 10.12263/DZXB.20210231
[12] 郭忠义, 潘珍珍, 龚超凡, 等. OAM光通信路由器件研究[J]. 通信学报, 2020, 41(11): 185−197. doi: 10.11959/j.issn.1000-436x.2020184
Guo Z Y, Pan Z Z, Gong C F, et al. Research on router device of OAM optical communication[J]. J Commun, 2020, 41(11): 185−197. doi: 10.11959/j.issn.1000-436x.2020184
[13] Kai C H, Huang P, Shen F, et al. Orbital angular momentum shift keying based optical communication system[J]. IEEE Photon J, 2017, 9(2): 7902510. doi: 10.1109/JPHOT.2017.2672642
[14] 郭忠义, 龚超凡, 刘洪郡, 等. OAM光通信技术研究进展[J]. 光电工程, 2020, 47(3): 90−123. doi: 10.12086/oee.2020.190593
Guo Z Y, Gong C F, Liu H J, et al. Research advances of orbital angular momentum based optical communication technology[J]. Opto-Electron Eng, 2020, 47(3): 90−123. doi: 10.12086/oee.2020.190593
[15] Chen Y, Gao J, Jiao Z Q, et al. Mapping twisted light into and out of a photonic chip[J]. Phys Rev Lett, 2018, 121(23): 233602. doi: 10.1103/PhysRevLett.121.233602
[16] Yang L, Qian D D, Xin C, et al. Direct laser writing of complex microtubes using femtosecond vortex beams[J]. Appl Phys Lett, 2017, 110(22): 221103. doi: 10.1063/1.4984744
[17] Masajada J, Popiołek-Masajada A, Wieliczka D M. The interferometric system using optical vortices as phase markers[J]. Opt Commun, 2002, 207(1–6): 85−93. doi: 10.1016/S0030-4018(02)01489-X
[18] Emile O, Emile J. Naked eye picometer resolution in a Michelson interferometer using conjugated twisted beams[J]. Opt Lett, 2017, 42(2): 354−357. doi: 10.1364/OL.42.000354
[19] Hemo E, Spektor B, Shamir J. Scattering of singular beams by subwavelength objects[J]. Appl Opt, 2011, 50(1): 33−42. doi: 10.1364/AO.50.000033
[20] 孙海滨, 孙平. 涡旋光用于物体面内位移变形测量的模拟[J]. 光电子·激光, 2014, 25(11): 2252−2258. doi: 10.16136/j.joel.2014.11.031
Sun H B, Sun P. Simulation of in-plane displacement deformation measurement using vortex beams[J]. J Optoelectron Laser, 2014, 25(11): 2252−2258. doi: 10.16136/j.joel.2014.11.031
[21] 孙海滨, 刘婷婷, 孙平. 光学涡旋应用于微测量的研究进展[J]. 激光杂志, 2015, 36(6): 8−11. doi: 10.14016/j.cnki.jgzz.2015.06.008
Sun H B, Liu T T, Sun P. Research progress of applications of optical vortex in micro-measurement[J]. Laser J, 2015, 36(6): 8−11. doi: 10.14016/j.cnki.jgzz.2015.06.008
[22] 张利宏, 沈锋, 兰斌. 涡旋光束轨道角动量在大气湍流传输下的特性分析[J]. 光电工程, 2020, 47(4): 190272. doi: 10.12086/oee.2020.190272
Zhang L H, Shen F, Lan B. Characteristic analysis of orbital angular momentum of vortex beam propagating in atmospheric turbulent[J]. Opto-Electronic Eng, 2020, 47(4): 190272. doi: 10.12086/oee.2020.190272
[23] 贺锋涛, 房伟, 张建磊, 等. 汉克-贝塞尔光束在各向异性海洋湍流中轨道角动量传输特性分析[J]. 光电工程, 2020, 47(6): 190591. doi: 10.12086/oee.2020.190591
He F T, Fang W, Zhang J L, et al. Analysis of the transmission characteristics of Hank-Bessel beam in anisotropic ocean turbulence[J]. Opto-Electronic Eng, 2020, 47(6): 190591. doi: 10.12086/oee.2020.190591
[24] Curtis J E, Koss B A, Grier D G. Dynamic holographic optical tweezers[J]. Opt Commun, 2002, 207(1–6): 169−175. doi: 10.1016/S0030-4018(02)01524-9
[25] Curtis J E, Grier D G. Modulated optical vortices[J]. Opt Lett, 2003, 28(11): 872−874. doi: 10.1364/OL.28.000872
[26] Curtis J E, Grier D G. Structure of optical vortices[J]. Phys Rev Lett, 2003, 90(13): 133901. doi: 10.1103/PhysRevLett.90.133901
[27] 朱艳英, 沈军峰, 窦红星, 等. 计算全息法获取高阶类贝塞尔光束的新设计[J]. 光电子·激光, 2011, 22(8): 1263−1268. doi: 10.16136/j.joel.2011.08.015
Zhu Y Y, Shen J F, Dou H X, et al. A new design of computer generated holography to obtain high order Bessel-like beam[J]. J Optoelectron Laser, 2011, 22(8): 1263−1268. doi: 10.16136/j.joel.2011.08.015
[28] 薄斌, 门克内木乐, 赵建林, 等. 用反射式纯相位液晶空间光调制器产生涡旋光束[J]. 光电子·激光, 2012, 23(1): 74−78. doi: 10.16136/j.joel.2012.01.014
Bo B, Neimule M, Zhao J L, et al. Generation of vortex beams with a reflected type phase only LCSLM[J]. J Optoelectron Laser, 2012, 23(1): 74−78. doi: 10.16136/j.joel.2012.01.014
[29] Beijersbergen M W, Coerwinkel R P C, Kristensen M, et al. Helical-wavefront laser beams produced with a spiral phaseplate[J]. Opt Commun, 1994, 112(5–6): 321−327. doi: 10.1016/0030-4018(94)90638-6
[30] Zhao Z, Wang J, Li S H, et al. Metamaterials-based broadband generation of orbital angular momentum carrying vector beams[J]. Opt Lett, 2013, 38(6): 932−934. doi: 10.1364/OL.38.000932
[31] Beijersbergen M W, Allen L, van der Veen H E L O, et al. Astigmatic laser mode converters and transfer of orbital angular momentum[J]. Opt Commun, 1993, 96(1–3): 123−132. doi: 10.1016/0030-4018(93)90535-D
[32] Lee C Y, Chang C C, Cho C Y, et al. Generation of higher order vortex beams from a YVo4/Nd: YVO4 self-Raman laser via off-axis pumping with mode converter[J]. IEEE J Sel Top Quantum Electron, 2015, 21(1): 1600305. doi: 10.1109/JSTQE.2014.2324754
[33] Tang A, Yu T, Zuo J, et al. Experimental research on a multi-aperture phase modulation technique based on a corner-cube reflector array[J]. Opt Express, 2022, 30(3): 3793−3803. doi: 10.1364/OE.448379
[34] 陈光明, 林惠川, 蒲继雄. 轴棱锥聚焦涡旋光束获得高阶贝塞尔光束[J]. 光电子·激光, 2011, 22(6): 945−950. doi: 10.16136/j.joel.2011.06.015
Chen G M, Lin H C, Pu J X. Generation of high-order Bessel beams by focusing vortex beams with an axicon[J]. J Optoelectron Laser, 2011, 22(6): 945−950. doi: 10.16136/j.joel.2011.06.015
[35] Ito A, Kozawa Y, Sato S. Generation of hollow scalar and vector beams using a spot-defect mirror[J]. J Opt Soc Am A, 2010, 27(9): 2072−2077. doi: 10.1364/JOSAA.27.002072
[36] Lin X J, Feng Q C, Zhu Y, et al. Diode-pumped wavelength-switchable visible Pr3+: YLF laser and vortex laser around 670 nm[J]. Opto-Electron Adv, 2021, 4(4): 210006. doi: 10.29026/oea.2021.210006
[37] Ngcobo S, Litvin I, Burger L, et al. A digital laser for on-demand laser modes[J]. Nat Commun, 2013, 4: 2289. doi: 10.1038/ncomms3289
[38] Aadhi A, Samanta G K, Kumar S C, et al. Controlled switching of orbital angular momentum in an optical parametric oscillator[J]. Optica, 2017, 4(3): 349−355. doi: 10.1364/OPTICA.4.000349
[39] Lu J L, Lin H F, Zhang G, et al. Direct generation of an optical vortex beam from a diode-pumped Yb: MgWO4 laser[J]. Laser Phys Lett, 2017, 14(8): 085807. doi: 10.1088/1612-202X/aa7878
[40] Hou T Y, Chang Q, Yu T, et al. Switching the orbital angular momentum state of light with mode sorting assisted coherent laser array system[J]. Opt Express, 2021, 29(9): 13428−13440. doi: 10.1364/OE.422635
[41] Braverman B, Skerjanc A, Sullivan N, et al. Fast generation and detection of spatial modes of light using an acousto-optic modulator[J]. Opt Express, 2020, 28(20): 29112−29121. doi: 10.1364/OE.404309
[42] Strain M J, Cai X L, Wang J W, et al. Fast electrical switching of orbital angular momentum modes using ultra-compact integrated vortex emitters[J]. Nat Commun, 2014, 5: 4856. doi: 10.1038/ncomms5856
[43] Jiang W H. Overview of adaptive optics development[J]. Opto-Electron Eng, 2018, 45(3): 170489. doi: 10.12086/oee.2018.170489
[44] 姜文汉, 杨泽平, 官春林, 等. 自适应光学技术在惯性约束聚变领域应用的新进展[J]. 中国激光, 2009, 36(7): 1625−1634. doi: 10.3788/CJL20093607.1625
Jiang W H, Yang Z P, Guan C L, et al. New progress on adaptive optics in inertial confinement fusion facility[J]. Chin J Laser, 2009, 36(7): 1625−1634. doi: 10.3788/CJL20093607.1625
[45] Baranova N B, Mamaev A V, Pilipetsky N F, et al. Wave-front dislocations: topological limitations for adaptive systems with phase conjugation[J]. J Opt Soc Am, 1983, 73(5): 525−528. doi: 10.1364/JOSA.73.000525
[46] Yu X M, Todi A, Tang H M. Bessel beam generation using a segmented deformable mirror[J]. Appl Opt, 2018, 57(16): 4677−4682. doi: 10.1364/AO.57.004677
[47] Ghai D P, Senthilkumaran P, Sirohi R S. Adaptive helical mirror for generation of optical phase singularity[J]. Appl Opt, 2008, 47(10): 1378−1383. doi: 10.1364/AO.47.001378
[48] Tyson R K, Scipioni M, Viegas J. Generation of an optical vortex with a segmented deformable mirror[J]. Appl Opt, 2008, 47(33): 6300−6306. doi: 10.1364/AO.47.006300
[49] Scipioni M, Tyson R K, Viegas J. Mode purity comparison of optical vortices generated by a segmented deformable mirror and a static multilevel phase plate[J]. Appl Opt, 2008, 47(28): 5098−5102. doi: 10.1364/AO.47.005098
[50] Bovino F A, Braccini M, Bertolotti M. Design of a programmable spiral phase mirror[Z]. arXiv: 1111.3483, 2012. https://doi.org/10.48550/arXiv.1111.3483.
[51] 唐奥, 兰斌, 沈锋. 基于连续镜面变形镜生成模式可调的涡旋光束仿真研究[J]. 光子学报, 2022, 51(1): 0151120. doi: 10.3788/gzxb20225101.0151120
Tang A, Lan B, Shen F. Simulation of generating vortex beam with controllable mode based on deformable mirror with continuous surface[J]. Acta Photon Sin, 2022, 51(1): 0151120. doi: 10.3788/gzxb20225101.0151120
[52] 杨平, 许冰, 姜文汉, 等. 遗传算法在自适应光学系统中的应用[J]. 光学学报, 2007, 27(9): 1628−1632. doi: 10.3321/j.issn:0253-2239.2007.09.017
Yang P, Xu B, Jiang W H, et al. Study of a genetic algorithm used in an adaptive optical system[J]. Acta Opt Sin, 2007, 27(9): 1628−1632. doi: 10.3321/j.issn:0253-2239.2007.09.017
[53] El-Agmy R, Bulte H, Greenaway A H, et al. Adaptive beam profile control using a simulated annealing algorithm[J]. Opt Express, 2005, 13(16): 6085−6091. doi: 10.1364/OPEX.13.006085
[54] Yang H Z, Li X Y, Gong C L, et al. Restoration of turbulence-degraded extended object using the stochastic parallel gradient descent algorithm: numerical simulation[J]. Opt Express, 2009, 17(5): 3052−3062. doi: 10.1364/OE.17.003052
[55] Alda J, Boreman G D. Zernike-based matrix model of deformable mirrors: optimization of aperture size[J]. Appl Opt, 1993, 32(13): 2431−2438. doi: 10.1364/AO.32.002431
[56] 张楠, 郭宋明, 卢佳琦, 等. 基于变形镜生成Airy光束特性研究[J]. 激光与光电子学进展, 2020, 57(15): 152601. doi: 10.3788/LOP57.152601
Zhang N, Guo S M, Lu J Q, et al. Characteristics of airy beams generated with deformable mirrors[J]. Laser Optoelectron Prog, 2020, 57(15): 152601. doi: 10.3788/LOP57.152601
[57] Débarre D, Booth M J, Wilson T. Image based adaptive optics through optimisation of low spatial frequencies[J]. Opt Express, 2007, 15(13): 8176−8190. doi: 10.1364/OE.15.008176
[58] 李新阳, 王春鸿, 鲜浩, 等. 自适应光学系统的实时模式复原算法[J]. 强激光与粒子束, 2002, 14(1): 53−56. doi: 10.1016/S0731-7085(02)00201-7
Li X Y, Wang C H, Xian H, et al. Real-time modal reconstruction algorithm for adaptive optics systems[J]. High Power Laser Part Beams, 2002, 14(1): 53−56. doi: 10.1016/S0731-7085(02)00201-7
[59] 闫伟, 陈志华, 杜太焦, 等. 基于变形镜本征模式法校正大气热晕的数值模拟[J]. 光学学报, 2014, 34(11): 1101001. doi: 10.3788/AOS201434.1101001
Yan W, Chen Z H, Du T J, et al. Numerical simulation of correction thermal blooming based on deformable mirror Eigen mode[J]. Acta Opt Sin, 2014, 34(11): 1101001. doi: 10.3788/AOS201434.1101001
[60] 喻际, 董冰. 基于变形镜本征模式的无波前传感器自适应光学系统实验研究[J]. 光学学报, 2015, 35(3): 0322004. doi: 10.3788/AOS201535.0322004
Yu J, Dong B. Experimental study of wavefront sensorless adaptive optics based on deformable mirror Eigen modes[J]. Acta Opt Sin, 2015, 35(3): 0322004. doi: 10.3788/AOS201535.0322004
[61] 梁佳新, 向汝建, 杜应磊, 等. 基于变形镜本征模式和远场测量的光束净化[J]. 强激光与粒子束, 2020, 32(8): 081002. doi: 10.11884/HPLPB202032.200082
Liang J X, Xiang R J, Du Y L, et al. Laser beam cleanup based on deformable-mirror Eigen modes and far-field measurement[J]. High Power Laser Part Beams, 2020, 32(8): 081002. doi: 10.11884/HPLPB202032.200082
[62] 李恩德, 戴云, 王海英, 等. 微加工薄膜变形镜本征模分析[J]. 强激光与粒子束, 2006, 18(8): 1265−1270.
Li E D, Dai Y, Wang H Y, et al. Eigen mode of micromachined membrane deformable mirror[J]. High Power Laser Part Beams, 2006, 18(8): 1265−1270.
[63] Shi Y, Wu Q W, Ming J. An archimedean spiral antenna for generation of tunable angular momentum wave[J]. IEEE Access, 2021, 9: 63122−63130. doi: 10.1109/ACCESS.2021.3074210
[64] Tao S H, Yuan X C, Lin J, et al. Fractional optical vortex beam induced rotation of particles[J]. Opt Express, 2005, 13(20): 7726−7731. doi: 10.1364/OPEX.13.007726
[65] Hu J T, Tai Y P, Zhu L H, et al. Optical vortex with multi-fractional orders[J]. Appl Phys Lett, 2020, 116(20): 201107. doi: 10.1063/5.0004692
[66] MacDonald M P, Paterson L, Volke-Sepulveda K, et al. Creation and manipulation of three-dimensional optically trapped structures[J]. Science, 2002, 296(5570): 1101−1103. doi: 10.1126/science.1069571
-
下载:
点击扫一扫
图(15)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
