Polarization regulation characteristics of reflected waves at the interface of double topological insulators
-
摘要
本文对两种三维强拓扑绝缘体分界面的反射极化现象进行了研究,得到了线偏振光完全转化的普适性充要条件。通过分析分界面的直接反射率、交叉反射率以及极化转化率,发现该模型利用现有的拓扑绝缘体材料就可以实现线极化波的完全转变,突破了需要新的较小介电常数的拓扑绝缘体材料才能完全转化的限制。该转化过程可以利用克尔旋转角进行验证,并给出了实现超强角稳定性的极化转化器件的设计思路。这为拓扑绝缘体在极化器件方面的应用提供了理论依据。

Abstract
The property of reflective polarization on the surface of two 3D strong topological insulators was studied, obtaining the generalized necessary conditions required for the complete polarization conversion of linearly polarized light. By analyzing the reflectivity, cross reflectivity, and polarization conversion ratios of the interface of two topological insulators, we found that the model can realize the complete polarization conversion by using the existing topological insulator material, breaking through the limitation that the complete conversion requires a new small dielectric constant topological insulator material. The process can be verified by the Kerr rotation angle. Finally, we show the design method of polarization conversion devices to realize super strong angular stability. The polarization control capability of topological insulators can also be verified by Kerr effect. This work provides a theoretical basis for the application of topological insulators in polarized devices.
-
Key words:
- topological insulator /
- polarization conversion /
- polarization control
-
Overview

Overview: Topological materials are new types of quantum metamaterials with metal surface states and insulator states that have been predicted and observed in recent years. The polarization conversion phenomenon caused by the Kerr effect and the Faraday effect of topological insulator can be used as a polarization-separation or polarization-conversion device, and thus it is important to study the polarization properties of the topological insulator.
Polarization, as one of the basic characteristics of electromagnetic waves, plays an important role in communication systems such as antennas. With the diversification of application scenarios, we need to control the polarization state of electromagnetic waves. Therefore, the exploration of the polarization performance of new materials is also a continuous and important subject. The current work of TI materials is limited to the common isotropic medium-topological insulator interface, which has strict requirements on the dielectric constant, and the current TI materials cannot meet it. Thus we discussed the polarization control performance of the double-topology insulator interface model, which has a certain tolerance for the dielectric constant of the material and can increase the selectivity of TI materials.
In this paper, an interface transmission model of plane wave oblique incidence to two topological insulators is established, and the linear polarization conversion characteristics of reflected waves are discussed. The calculation results prove that the model can achieve complete transformation of polarization under certain parameter settings, and the polarization conversion property can be explained by Kerr effect. Besides, we show the design method of polarization conversion devices to realize super strong angular stability. This research provides a theoretical reference for the application of topological insulators in polarized devices.
-

-
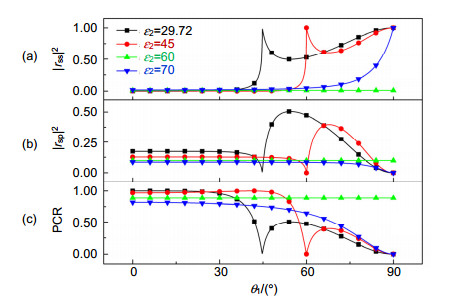
图 2 TI1-TI2界面处s波斜入射时反射场中极化转变结果,ε1=60。(a) 直接反射率|rss|2;(b) 交叉反射率|rsp|2;(c) 极化转化率
Figure 2. The results of the polarization conversion in the reflection field at the oblique incidence of the s-wave at the TI1-TI2 interface when ε1=60. (a) Direct reflectivity |rss|2; (b) Cross-polarized reflectivity |rsp|2; (c) Polarization conversion ratios (PCR)
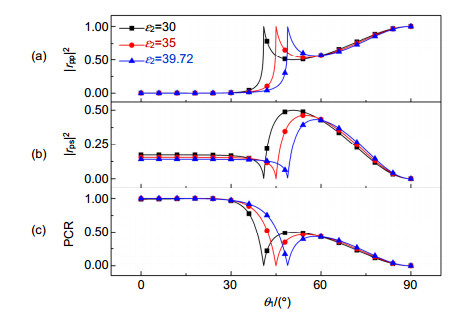
图 3 ε2>ε1>0条件下,TI1-TI2界面处pp波斜入射时反射场中的极化转变结果,ε1=31。(a) 直接反射率|rpp|2;(b) 交叉反射率|rps|2;(c) 极化转化率PCR
Figure 3. Under the condition of ε2>ε1>0, results of the polarization conversion in the reflection field at the oblique incidence of the p-wave at the TI1-TI2 interface when ε1=31. (a) Direct reflectivity |rpp|2; (b) Cross-polarized reflectivity |rps|2; (c) Polarization conversion ratios(PCR)
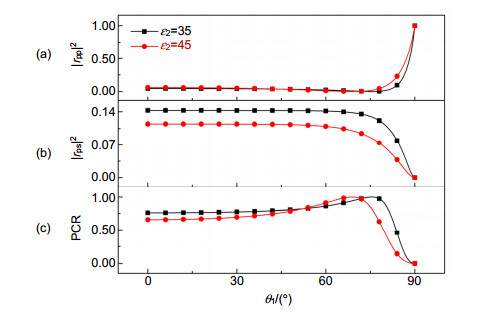
图 4 ε2≤ε1-7.57N2条件下,TI1-TI2界面处p波斜入射时反射场中极化转变结果,ε1=70。(a) 直接反射率|rpp|2;(b) 交叉反射率|rps|2;(c) 极化转化率(PCR)
Figure 4. Under the condition of ε2≤ε1-7.57N2, results of the polarization conversion in the reflection field at the oblique incidence of the p-wave at the TI1-TI2 interface when ε1=70. (a) Direct reflectivity |rpp|2; (b) Cross-polarized reflectivity |rps|2; (c) Polarization conversion ratios(PCR)
-
参考文献
[1] 张建华, 黄冶. 电磁波极化的应用[J]. 大学物理, 2012, 31(3): 52–54. https://www.cnki.com.cn/Article/CJFDTOTAL-DXWL201203015.htm
Zhang J H, Huang Y. Applications of electromagnetic wave polarization[J]. Coll Phys, 2012, 31(3): 52–54. https://www.cnki.com.cn/Article/CJFDTOTAL-DXWL201203015.htm
[2] 陈龙天, 程用志, 聂彦, 等. 人工异向介质调控电磁波极化特性的实验与仿真研究[J]. 物理学报, 2012, 61(9): 094203. https://www.cnki.com.cn/Article/CJFDTOTAL-WLXB201209034.htm
Chen L T, Cheng Y Z, Nie Y, et al. Study on measurement and simulation of manipulating electromagnetic wave polarization by metamaterials[J]. Acta Phys Sin, 2012, 61(9): 094203. https://www.cnki.com.cn/Article/CJFDTOTAL-WLXB201209034.htm
[3] Moore J E. The birth of topological insulators[J]. Nature, 2010, 464(7286): 194–198. doi: 10.1038/nature08916
[4] Yue Z J, Cai B Y, Wang L, et al. Intrinsically core-shell plasmonic dielectric nanostructures with ultrahigh refractive index[J]. Sci Adv, 2016, 2(3): e1501536. doi: 10.1126/sciadv.1501536
[5] Chang C Z, Zhang J S, Feng X, et al. Experimental observation of the quantum anomalous hall effect in a magnetic topological insulator[J]. Science, 2013, 340(6129): 167–170. doi: 10.1126/science.1234414
[6] He K, Wang Y Y, Xue Q K. Topological insulator and the quantum anomalous Hall effect[J]. Chin Sci Bull, 2014, 59(35): 3431–3441. doi: 10.1360/N972014-00938
[7] Qi X L, Hughes T L, Zhang S C. Topological field theory of time-reversal invariant insulators[J]. PhysRev B, 2008, 78(19): 195424. http://nsr.oxfordjournals.org/external-ref?access_num=10.1103/PhysRevB.78.195424&link_type=DOI
[8] 钱栋梁, 陈良尧, 郑卫民, 等. 一种完整测量磁光克尔效应和法拉第效应的方法[J]. 光学学报, 1999, 19(4): 474–480. doi: 10.3321/j.issn:0253-2239.1999.04.008
Qian D L, Chen L Y, Zheng W M, et al. A method to measure completely the magneto-optical kerr and faraday effects[J]. Acta Opt Sin, 1999, 19(4): 474–480. doi: 10.3321/j.issn:0253-2239.1999.04.008
[9] Lan Y P, Wan S L, Zhang S C. Generalized quantization condition for topological insulators[J]. Phys Rev B, 2011, 83(20): 205109. doi: 10.1103/PhysRevB.83.205109
[10] Fleet L. Topological transistor[J]. Nat Phys, 2015, 11(1): 5.
[11] Mahoney A C, Colless J I, Peeters L, et al. Zero-field edge plasmons in a magnetic topological insulator[J]. Nat Comm, 2017, 8(1): 1836. doi: 10.1038/s41467-017-01984-5
[12] 王明军, 林妞妞. 拉盖尔-高斯光束在含拓扑绝缘体周期薄膜中的传输特性[J]. 中国激光, 2020, 47(1): 105003. https://www.cnki.com.cn/Article/CJFDTOTAL-JJZZ202001024.htm
Wang M J, Lin N N. Propagation characteristics of laguerre-gaussian beams in periodic films with topological insulators[J]. Chin J Lasers, 2020, 47(1): 105003. https://www.cnki.com.cn/Article/CJFDTOTAL-JJZZ202001024.htm
[13] Yang Y, Gao Z, Xue H R, et al. Realization of a three-dimensional photonic topological insulator[J]. Nature, 2019, 565(7741): 622–626. doi: 10.1038/s41586-018-0829-0
[14] 陈芳芳. 拓扑绝缘体界面的透射极化旋转[J]. 通信技术, 2019, 52(9): 2087–2091. doi: 10.3969/j.issn.1002-0802.2019.09.004
Chen F F. Transmission polarization rotation of topological insulator interface[J]. Comm Technol, 2019, 52(9): 2087–2091. doi: 10.3969/j.issn.1002-0802.2019.09.004
[15] Liu F, Xu J P, Yang Y P. Polarization conversion of reflected electromagnetic wave from topological insulator[J]. J Opt Soc Am B, 2014, 31(4): 735–741. doi: 10.1364/JOSAB.31.000735
[16] Chang M C, Yang M F. Optical signature of topological insulators[J]. Phys Rev B, 2009, 80(11): 113304. doi: 10.1103/PhysRevB.80.113304
[17] Zuo Z W, Ling D B, Sheng L, et al. Optical properties for topological insulators with metamaterials[J]. Phys Lett A, 2013, 377(40): 2909–2915. doi: 10.1016/j.physleta.2013.09.004
[18] Huang X J, Chen J, Yang H L. High-efficiency wideband reflection polarization conversion metasurface for circularly polarized waves[J]. J Appl Phys, 2017, 122(4): 043102. doi: 10.1063/1.4996643
[19] Tse W K, MacDonald A H. Giant Magneto-optical kerr effect and universal faraday effect in thin-film topological insulators[J]. Phys Rev Lett, 2010, 105(5): 057401. doi: 10.1103/PhysRevLett.105.057401
[20] 张玉平, 唐利斌. 拓扑绝缘体光电探测器研究进展[J]. 红外技术, 2020, 42(1): 1–9. https://www.cnki.com.cn/Article/CJFDTOTAL-HWJS202001002.htm
Zhang Y P, Tang L B. Research progress in photodetectors based on topological insulators[J]. Infrared Technol, 2020, 42(1): 1–9. https://www.cnki.com.cn/Article/CJFDTOTAL-HWJS202001002.htm
-
访问统计


 E-mail Alert
E-mail Alert RSS
RSS

 下载:
下载: