E-mail Alert
RSS
Modal wavefront reconstruction to obtain Zernike coefficient with no cross coupling in lateral shearing measurement
-
摘要:
模式耦合误差常见于横向剪切干涉测量中基于波前梯度数据的模式复原法，其原因是用于表示波前的基函数——Zernike圆多项式的导数不正交。使用一种含有Gram矩阵的矩阵方程进行复原，直接利用Zernike圆多项式m≠0模式角向导数对于权重函数w(ρ) = ρ (极坐标下)的正交性，以及Zernike圆多项式m = 0模式径向导数对于权重函数w(ρ) = ρ(1-ρ2)(极坐标下)的正交性进行复原。该方法无需构造辅助的向量函数，并可得到无耦合的Zernike系数，复原结果表明，模式耦合得到了避免。该方法可推广到环上，得到无耦合的Zernike环多项式系数。
-
关键词:
- Zernike圆多项式 /
- Zernike环多项式 /
- 剪切干涉 /
- 波前复原 /
- 模式耦合
Abstract:Modal cross coupling frequently occurs in modal approaches from wavefront gradient data such as lateral shearing measurement through Zernike circle polynomials, since the gradients of Zernike circle polynomials are not orthogonal. We use a modal approaches incorporating the Gram matrix, using the orthogonality of angular derivative of m≠0 modes with respect to weight function w(ρ) = ρ (polar coordinates), and the orthogonality of radial derivative of m = 0 modes with respect to weight function w(ρ) = ρ(1-ρ2) (polar coordinates). The Gram matrix method needs no auxiliary vector functions. The Zernike coefficients can be obtained with no modal cross coupling. The simulation results are given, which indicate that the modal cross coupling is avoided by using Gram matrix method. This method can be easily extended to annulus, and the coefficients of Zernike annular polynomials with no modal cross coupling can be obtained.
-
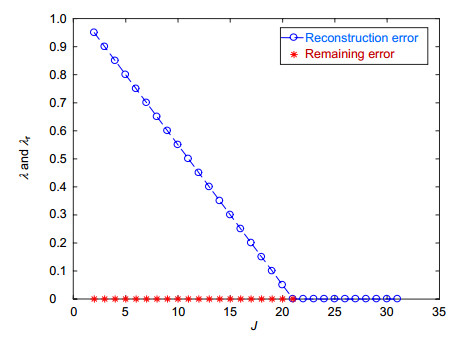
Overview: Modal cross coupling frequently occurs in modal approaches from wavefront gradient data such as lateral shearing measurement through Zernike circle polynomials, since the gradients of Zernike circle polynomials are not orthogonal. We use a modal approach incorporating the Gram matrix, instead of least squares estimation, to reconstruct coefficients of modes for high sampling gradient measurement such as lateral shearing measurement. The matrix equation incorporating the Gram matrix has exactly one solution when the modes of the Gram matrix are linearly dependent. The matrix equation incorporating the Gram matrix has the solution without modal cross coupling when the modes of the Gram matrix are mutually orthogonal with respect to the same weight function of the Gram matrix. Using the orthogonality of angular derivative of m≠0 modes with respect to weight function w(ρ) = ρ (polar coordinates), one can obtain Zernike coefficients of m≠0 modes without modal cross coupling by Gram matrix method. Using the orthogonality of radial derivative of m = 0 modes with respect to weight function w(ρ) = ρ(1-ρ2) (polar coordinates), one can obtain Zernike coefficients of m≠0 modes without modal cross coupling by Gram matrix method. The Gram matrix method needs no auxiliary vector functions, and can be easily constructed and calculated. The Zernike coefficients can be obtained with no modal cross coupling. The numerical simulation results are given. Remaining error can characterize the modal cross coupling when sampling number is sufficiently high so that modal aliasing is able to be neglected. The numerical simulation result shows that the remaining error keeps very small as the truncation number J changes. The result indicates that the modal cross coupling is avoided by using Gram matrix method. This method can be easily generalized to annulus, one can obtain Zernike annular polynomial coefficients with no modal cross coupling.
-
-
图 1 波前复原误差λ和残差λr与截断数J的关系，运用本文所述式(18)与式(19)的Gram矩阵方法
Figure 1. Reconstruction error λ and remaining error λr versus truncation of reconstruction modes J, by Gram matrix method in Eq.(18) and Eq.(19)
图 2 波前复原误差λ和残差λr与截断数J的关系，运用式(1) Gram矩阵方法，权重函数w(ρ) = ρ (极坐标)
Figure 2. Reconstruction error λ and remaining error λr versus truncation of reconstruction modes J, by Gram matrix method in Eq.(1), w(ρ) = ρ (polar coordinate)
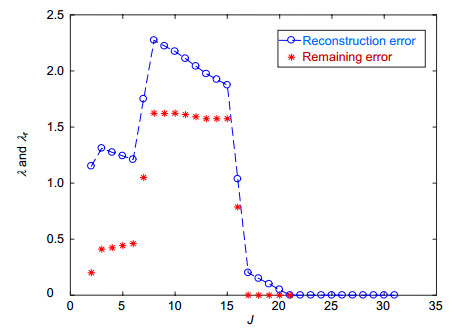
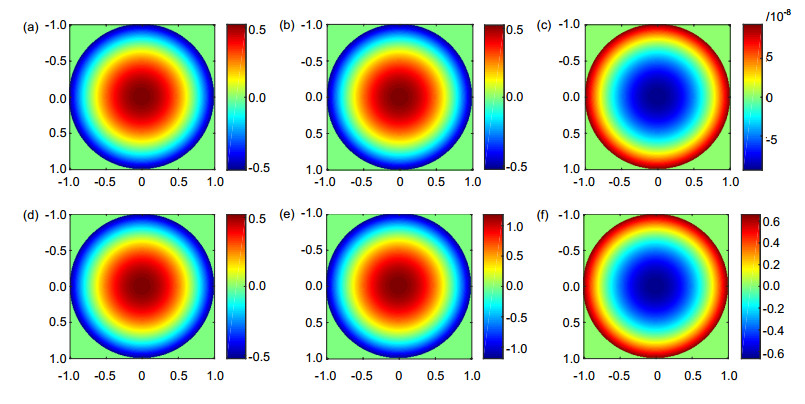
图 3 波前复原结果。(a)原始波前；(b)式(18)复原的m≠0项的波前；(c)式(19)复原的m = 0项的波前；(d)复原波前；(e)复原残留误差
Figure 3. Reconstruction results. (a) Original wavefront; (b) Reconstructed wavefront by Eq.(18), including m≠0 modes; (c) Reconstructed wavefront by Eq.(19), including m = 0 modes; (d) Reconstructed wavefront; (e) Residual error
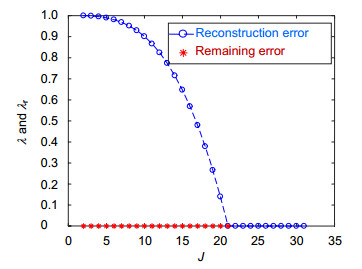
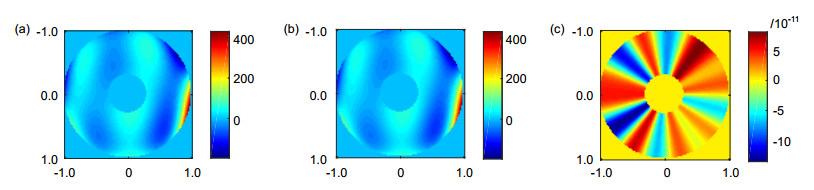
图 5 波前复原结果。 运用本文所述式(19)的 Gram 矩阵方法。 (a) Zernike 离焦项 Z20 的复原波前， 截断数 J=4； (b) Zernike 离焦项 Z20 的复原波前，截断数 J=2； (c) 复原残留误差原。运用式(1)的 Gram 矩阵方法： (d) Zernike 离焦项 Z20 的复原波前，截断数 J=4； (e) Zernike 离焦项 Z20 的复原波前，截断数 J=2； (f) 复原残留误差原
Figure 5. Reconstruction results by Gram matrix method in Eq.(19). (a) Reconstructed wavefront of Z20 , where truncation number J=4; (b) Reconstructed wavefront of Z20 , where truncation number J=2; (c) Residual error. Reconstruction results by Gram matrix method in Eq.(1); (d) Reconstructed wavefront of Z20 , where truncation number J=4; (e) Reconstructed wavefront of Z20 , where truncation number J=2; (f) Residual error
图 6 波前复原误差和残差λr与截断数J的关系
Figure 6. Reconstruction error and remaining error λr versus truncation of reconstruction modes J
-
[1] Rimmer M P. Method for evaluating lateral shearing interferograms[J]. Applied Optics, 1974, 13(3): 623–629. doi: 10.1364/AO.13.000623
[2] Harbers G, Kunst P J, Leibbrandt G W R. Analysis of lateral shearing interferograms by use of Zernike polynomials[J]. Applied Optics, 1996, 35(31): 6162–6172. doi: 10.1364/AO.35.006162
[3] Shen W, Chang M W, Wan D S. Zernike polynomial fitting of lateral shearing interferometry[J]. Optical Engineering, 1997, 36(36): 905–913. doi: 10.1117/1.601600
[4] Hunt B R. Matrix formulation of the reconstruction of phase values from phase differences[J]. Journal of the Optical Society of America, 1979, 69(3): 393–399. doi: 10.1364/JOSA.69.000393
[5] 姜文汉.自适应光学发展综述[J].光电工程, 2018, 45(3): 170489 doi: 10.12086/oee.2018.170489
Jiang W H. Overview of adaptive optics development[J]. Opto-Electronic Engineering, 2018, 45(3): 170489. doi: 10.12086/oee.2018.170489
[6] Tyson R. Principles of Adaptive Optics[M]. 3rd ed. London: CRC Press, 2010: 111–176.
[7] 张强, 姜文汉, 许冰.利用Zernike多项式对湍流波前进行波前重构[J].光电工程, 1998, 25(6): 15–19. doi: 10.1088/0256-307X/16/12/025
Zhang Q, Jiang W H, Xu B. Reconstruction of turbulent optical wavefront realized by Zernike polynomial[J]. Opto-Electronic Engineering, 1998, 25(6): 15–19. doi: 10.1088/0256-307X/16/12/025
[8] 鲜浩, 李华贵, 姜文汉, 等.用Hartmann－Shack传感器测量激光束的波前相位[J].光电工程, 1995, 22(2): 38–45. http://www.cnki.com.cn/Article/CJFDTOTAL-GDGC502.003.htm
Xian H, Li H G, Jiang W H, et al. Measurement of the wavefront phase of a laser beam with Hartmann-Shack sensor[J]. Opto-Electronic Engineering, 1995, 22(2): 38–45. http://www.cnki.com.cn/Article/CJFDTOTAL-GDGC502.003.htm
[9] 张锐, 杨金生, 田雨, 等.焦面哈特曼传感器波前相位复原[J].光电工程, 2013, 40(2): 32–39. doi: 10.3969/j.issn.1003-501X.2013.02.005
Zhang R, Yang J S, Tian Y, et al. Wavefront phase recovery from the plenoptic camera[J]. Opto-Electronic Engineering, 2013, 40(2): 32–39. doi: 10.3969/j.issn.1003-501X.2013.02.005
[10] Cubalchini R. Modal wave-front estimation from phase derivative measurements[J]. Journal of the Optical Society of America, 1979, 69(7): 972–977. doi: 10.1364/JOSA.69.000972
[11] Herrmann J. Cross coupling and aliasing in modal wave-front estimation[J]. Journal of the Optical Society of America, 1981, 71(8): 989–992. doi: 10.1364/JOSA.71.000989
[12] Huang S Y, Xi F J, Liu C H, et al. Eigenfunctions of Laplacian for phase estimation from wavefront gradient or curvature sensing[J]. Optics Communications, 2011, 284(12): 2781–2783. doi: 10.1016/j.optcom.2011.02.045
[13] Huang S Y, Xi F J, Liu C H, et al. Phase retrieval on annular and annular sector pupils by using the eigenfunction method to solve the transport of intensity equation[J]. Journal of the Optical Society of America A, 2012, 29(4): 513–520. doi: 10.1364/JOSAA.29.000513
[14] Huang S Y, Yu N, Xi F J, et al. Modal wavefront reconstruction with Zernike polynomials and eigenfunctions of Laplacian[J]. Optics Communications, 2013, 288: 7–12. doi: 10.1016/j.optcom.2012.09.067
[15] Gavrielides A. Vector polynomials orthogonal to the gradient of Zernike polynomials[J]. Optics Letters, 1982, 7(11): 526–528. doi: 10.1364/OL.7.000526
[16] Zhao C Y, Burge J H. Orthonormal vector polynomials in a unit circle, Part Ⅰ: basis set derived from gradients of Zernike polynomials[J]. Optics Express, 2007, 15(26): 18014–18024. doi: 10.1364/OE.15.018014
[17] Zhao C Y, Burge J H. Orthonormal vector polynomials in a unit circle, Part Ⅱ: completing the basis set[J]. Optics Express, 2008, 16(9): 6586–6591. doi: 10.1364/OE.16.006586
[18] Mahajan V N, Acosta E. Vector polynomials for direct analysis of circular wavefront slope data[J]. Journal of the Optical Society of America A, 2017, 34(10): 1908–1913. doi: 10.1364/JOSAA.34.001908
[19] Sun W H, Wang S, He X, et al. Jacobi circle and annular polynomials: modal wavefront reconstruction from wavefront gradient[J]. Journal of the Optical Society of America A, 2018, 35(7): 1140–1148. doi: 10.1364/JOSAA.35.001140
[20] Horn R A, Johnson C R. Matrix Analysis[M]. Cambridge: Cambridge University Press, 1990: 407.
[21] Mahajan V N. Zernike circle polynomials and optical aberrations of systems with circular pupils[J]. Applied Optics, 1994, 33(34): 8121–8124. doi: 10.1364/AO.33.008121
[22] Zernike F. Diffraction theory of the knife-edge test and its improved form, the phase-contrast method[J]. Monthly Notices of the Royal Astronomical Society, 2002, 94(2): 377–384. doi: 10.1117/1.1488608
[23] Born M, Wolf E. Principles of Optics[M]. 7th ed. Cambridge: Cambridge University Press, 1999: 905–910.
[24] Wang Z X, Guo D R. Special Functions[M]. Singapore: World Scientific, 1989: 139,169–173.
[25] Andrews G E, Askey R, Roy R. Special Functions[M]. Cambridge: Cambridge University Press, 1999: 94.
[26] Mahajan V N. Zernike annular polynomials and optical aberrations of systems with annular pupils[J]. Applied Optics, 1994, 33(34): 8125–8127. doi: 10.1364/AO.33.008125
-
下载:
点击扫一扫
图(7)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
