E-mail Alert
RSS
Simplification of locomotive running gear three-dimensional point cloud based on non-uniform division
-
摘要
激光线结构光扫描仪得到的三维点云数据具有冗余性，本文设计实现了一种基于两阶非均匀划分的点云精简算法对机车走行部数据进行处理。首先，根据内在形状特征算法估计出检测对象的点云法矢，并提取出点云特征点；其次，根据特征点云的分布对点云进行第一次非均匀划分，得到不均匀的初始点云块；最后，将划分后的各点云块映射到不同的高斯球中进行进一步细分，在高斯球面上进行均值漂移聚类，提取出每个聚类簇在实际三维空间中的重心，重心的集合即为精简结果。实验证明了方法的有效性，相比于现有的方法，本文中的方法在保证精度的前提下能够达到很高的精简率和运算效率，更契合机车自动化在线检测的需要。
Abstract
The 3D point cloud data obtained from the laser line structured light scanner has redundancy, and a point cloud simplification algorithm based on the two order non-uniform partition is designed and implemented to deal with locomotive running department in this paper. First, according to the intrinsic shape signature (ISS), the point cloud normal vector of the detected object are estimated and the feature points of the point cloud are extracted. Then, according to the distribution of the feature point cloud, the point cloud is first divided non-uniformly to obtain uneven initial cloud patches. Finally, the divided cloud points are mapped to different Gaussian spheres for further subdivision. The mean shift clustering is performed on the Gauss sphere to extract the center of gravity of each cluster in the actual three-dimensional space. The set of the center of gravity is the result of simplification. Experimental results verified the effectiveness of the proposed method. It can keep the details information of the point cloud while ensuring a high simplification rate. Comparing with the existing method, this method balances the speed and accuracy, and is more suitable for the on-line locomotive automated detection system.
-
Key words:
- point cloud simplification /
- non-uniform division /
- Gauss mapping /
- mean shift
-
Overview
Overview: With the increasing mileage of high-speed rail, railway locomotive safety testing is more and more important. Laser 3D scanning is a new type of detection method, which is expected to apply to the railway locomotive automated detection system. However, the point cloud obtained by 3D scanner usually contains a lot of redundant information, and the amount of data is usually too large to transmission and processing. Therefore, it is of great significance to study the simplification of 3D point cloud data. For the locomotive 3D point cloud data obtained by line-structured laser scanner, a point cloud simplification algorithm based on two order non-uniform partition is designed and implemented to process the point cloud data of locomotive running points in this paper. First, using K-d tree to reconstruct topological relations for discrete point clouds. Secondly, according to the intrinsic shape signature(ISS), we estimate the point cloud normal vector of the detected object and extract the feature points of the point cloud. The feature points are extracted by analyzing the neighborhood covariance matrix of the points, and the weight values are established to compensate the non-uniform downsampling of the 3D point cloud. Then, according to the distribution of the feature point cloud, the point cloud is divided non-uniformly to obtain uneven initial cloud patches. Finally, according to the normal vector information, the initially divided cloud points are mapped into different Gaussian spheres. The flat area of point cloud is mapped to a densely distributed cluster, and regions containing complex details are mapped to many different clusters. Second division based on mean-shift clustering is performed on the Gaussian sphere to extract the center of gravity of each cluster in the actual three-dimensional space. The set of points closest to the center of gravity is the result of simplification. Compared with the results of non-uniform grid method and K-means method, this algorithm achieves results in more than ten seconds in point cloud objects with a processing capacity of over one million, and the reduction rate can reach more than 90%. Speed is guaranteed. The points reserved in the flat area are relatively sparse, while the points reserved in the detail area are more precise. The maximum error of the reduced model is 2.5078 mm, and the average error is 0.3046 mm. Both are smaller than the other two algorithms and the accuracy is guaranteed. Therefore, the simplified data using the algorithm proposed in this paper can better detect defects on the surface of the object.
-
-
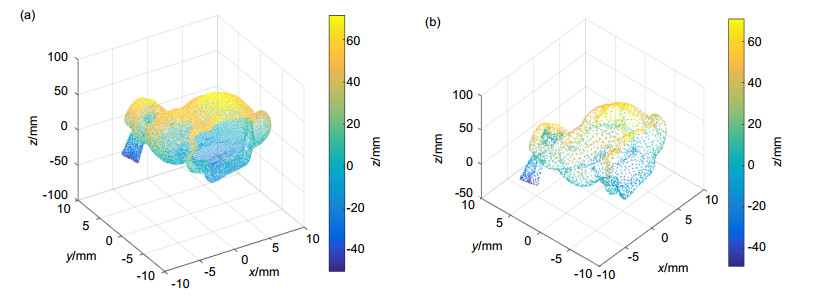
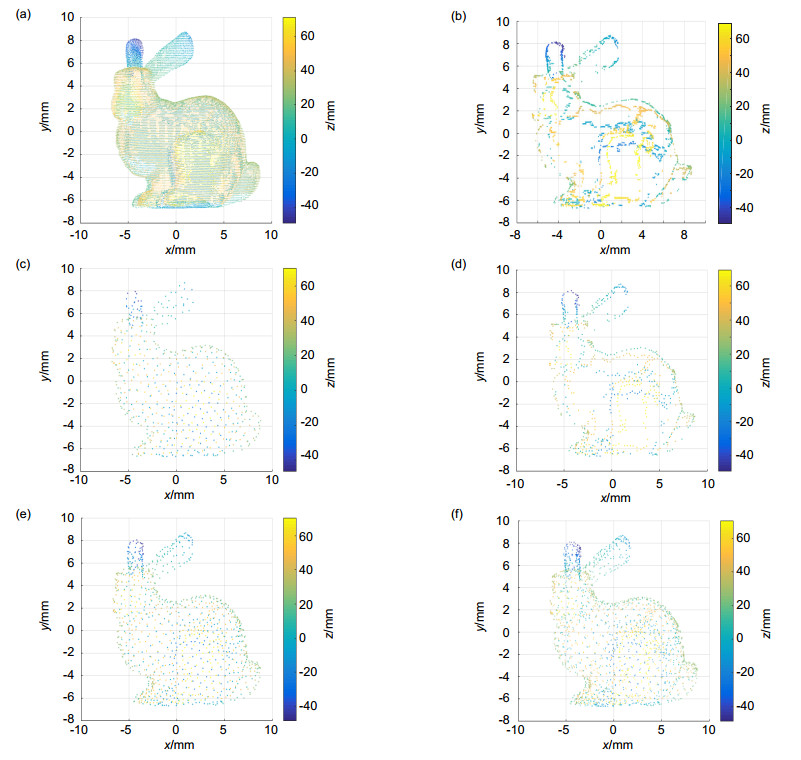
图 1 (a) 原始点云；(b)特征点选取结果；(c)均匀种子点；(d)特征种子点；(e)点云非均匀分块结果；(f)精简后的点云
Figure 1. Process of point cloud simplification in this paper. (a) Original point cloud; (b) Selection of feature points; (c) Uniform seed point; (d) Characteristic seed points; (e) Results of point cloud non-uniform block; (f) Simplification result
图 2 目标点云精简前后的对比。(a)精简前；(b)精简后
Figure 2. Comparison before and after simplification. (a) Before simplification; (b) After simplification
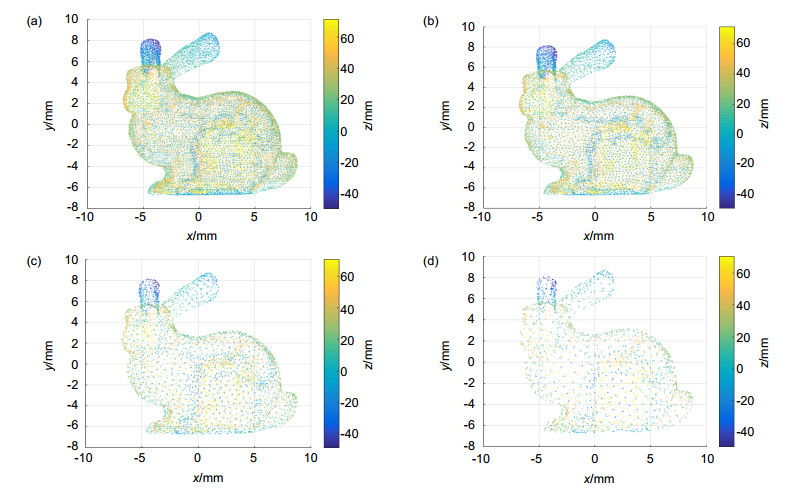
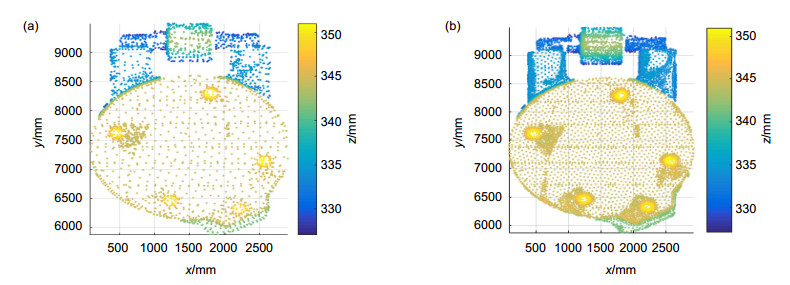
图 3 本文方法精简结果。(a) 44.76%精简率的结果；(b) 60.33%精简率的结果；(c) 82.11%精简率的结果；(d) 90.47%精简率的结果
Figure 3. Results of the simplification of proposed algorithm. (a) Result of 44.76% simplification rate; (b) Result of 60.33% simplification rate; (c) Result of 82.11% simplification rate; (d) Result of 90.47% simplification rate
图 5 非均匀网格法的精简结果。(a) 90.26%精简率的精简结果；(b) 67.30%精简率的精简结果
Figure 5. Simplification results of non-uniform grid. (a) 90.26% simplification rate; (b) 67.30% simplification rate
图 6 K-means聚类精简法的精简结果。(a) 90.55%精简率的结果；(b) 67.24%精简率的结果
Figure 6. Simplification results of K-means clustering. (a) 90.55% simplification rate; (b) 67.24% simplification rate
图 7 本文方法中的精简结果。(a) 90.66%精简率的结果；(b) 67.45%精简率的结果
Figure 7. Simplification results of proposed algorithm. (a) 90.66% simplification rate; (b) 67.45% simplification rate
图 8 三种算法精简误差比较。(a)最大误差；(b)平均误差
Figure 8. Comparison of simplification error of three algorithms. (a) Maximum error; (b) Average error
表 1 精简结果对比
Table 1. Marison of results of simplification
Proposed algorithm Non-uniform grid K-means clustering Test 1 Test 2 Test 1 Test 2 Test 1 Test 2 The number of points before simplification 36482 36482 36482 36482 36482 36482 The number of points after simplification 3406 11875 3532 11928 3448 11951 Simplification rate/% 90.66 67.45 90.26 67.30 90.55 67.24 δmax/mm 2.5078 1.0654 5.9874 3.3169 2.6405 2.1008 δavg/mm 0.3046 0.1765 0.5261 0.2675 0.3604 0.1965 Operation time/s 15.8764 8.2397 28.9074 19.1817 94.9914 69.3424 
下载: 导出CSV
-
参考文献
[1] Pendry J B. Negative refraction makes a perfect lens[J]. Physical Review Letters, 2000, 85(18): 3966-3969. doi: 10.1103/PhysRevLett.85.3966
[2] 张滋黎, 邾继贵, 周虎, 等.一种新型自动激光经纬仪引导跟踪方法[J].光电工程, 2010, 37(4): 1-7. doi: 10.3969/j.issn.1003-501X.2010.04.001
Zhang Z L, Zhu J G, Zhou H. Guidance tracking method of a new automatic laser theodolite system[J]. Opto-electronic Engineering, 2010, 37(4): 1-7. doi: 10.3969/j.issn.1003-501X.2010.04.001
[3] Yamamoto S. Development of inspection robot for nuclear power plant[C]//Proceedings of the 1992 IEEE International Conference on Robotics and Automation, Nice, France, 1992, 2: 1559-1566.
[4] Wang G H, Hu Z Y, Wu F C, et al. Implementation and experimental study on fast object modeling based on multiple structured stripes[J]. Optics and Lasers in Engineering, 2004, 42(6): 627-638. doi: 10.1016/j.optlaseng.2004.05.008
[5] 龙玺, 钟约先, 李仁举, 等.结构光三维扫描测量的三维拼接技术[J].清华大学学报(自然科学版), 2002, 42(4): 477-480. doi: 10.3321/j.issn:1000-0054.2002.04.014
Long X, Zhong Y X, Li R J, et al. 3-D surface integration in structured light 3-D scanning[J]. Journal of Tsinghua University (Science and Technology), 2002, 42(4): 477-480. doi: 10.3321/j.issn:1000-0054.2002.04.014
[6] 黄潜, 王泽勇, 李金龙, 等.基于三维扫描的机车走行部螺栓识别与定位[J].光电工程, 2018, 45(1): 170532. doi: 10.12086/oee.2018.170532
Huang Q, Wang Z Y, Li J L, et al. Automatic recognition of bolts on locomotive running gear based on laser scanner 3D measurement[J]. Opto-electronic Engineering, 2018, 45(1): 170532. doi: 10.12086/oee.2018.170532
[7] Maglo A, Courbet C, Alliez P, et al. Progressive compression of manifold polygon meshes[J]. Computers & Graphics, 2012, 36(5): 349-359.
[8] Luebke D P. A developer's survey of polygonal simplification algorithms[J]. IEEE Computer Graphics and Applications, 2001, 21(3): 24-35.
[9] Cignoni P, Montani C, Scopigno R, et al. A comparison of mesh simplification algorithms[J]. Computers & Graphics, 1998, 22(1): 37-54.
[10] Han H Y, Han X, Sun F S, et al. Point cloud simplification with preserved edge based on normal vector[J]. Optik - International Journal for Light and Electron Optics, 2015, 126(19): 2157-2162. doi: 10.1016/j.ijleo.2015.05.092
[11] Yu Z W, Wong H S, Peng H, et al. ASM: An adaptive simplification method for 3D point-based models[J]. Computer-Aided Design, 2010, 42(7): 598-612. doi: 10.1016/j.cad.2010.03.003
[12] Weir D J, Milroy M J, Bradley C, et al. Reverse engineering physical models employing wrap‐around B‐spline surfaces and quadrics[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 1996, 210(22): 147-157. http://d.old.wanfangdata.com.cn/NSTLQK/10.1243-PIME_PROC_1996_210_100_02/
[13] Martin R, Stroud I, Marshall A D. Data reduction for reverse engineering[J]. RECCAD, Deliverable Document 1 COPERNICUS Project, 1997, 1068: 85-100. http://d.old.wanfangdata.com.cn/OAPaper/oai_doaj-articles_153a763418c326439c21703e987041c5
[14] Lee K H, Woo H, Suk T. Point data reduction using 3D grids[J]. The International Journal of Advanced Manufacturing Technology, 2001, 18(3): 201-210. doi: 10.1007/s001700170075
[15] Shi B Q, Liang J, Liu Q. Adaptive simplification of point cloud using k-means clustering[J]. Computer-Aided Design, 2011, 43(8): 910-922. doi: 10.1016/j.cad.2011.04.001
[16] 袁小翠, 吴禄慎, 陈华伟.特征保持点云数据精简[J].光学精密工程, 2015, 23(9): 2666-2676. http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201509030
Yuan X C, Wu L S, Chen H W. Feature preserving point cloud simplification[J]. Optics and Precision Engineering, 2015, 23(9): 2666-2676. http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201509030
[17] Zhong Y. Intrinsic shape signatures: A shape descriptor for 3D object recognition[C]//Proceedings of the 2009 IEEE International Conference on Computer Vision Workshops, 2009: 689-696.
[18] 傅思勇, 吴禄慎, 陈华伟.空间栅格动态划分的点云精简方法[J].光学学报, 2017, 37(11): 1115007. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QKC20172017121900046644
Fu S Y, Wu L S, Chen H W. Point cloud simplification method based on space grid dynamic partitioning[J]. Acta Optica Sinica, 2017, 37(11): 1115007. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QKC20172017121900046644
[19] Hoppe H, Derose T, Duchamp T, et al. Surface reconstruction from unorganized points[J]. ACM SIGGRAPH Computer Graphics, 1992, 26(2): 71-78. http://d.old.wanfangdata.com.cn/Periodical/jsjfzsjytxxxb200310018
[20] Wang Y H, Hao W, Ning X J, et al. Automatic segmentation of urban point clouds based on the Gaussian map[J]. The Photogrammetric Record, 2013, 28(144): 342-361. doi: 10.1111/phor.2013.28.issue-144
-
访问统计
点击扫一扫
图(8)
表(1)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
