E-mail Alert
RSS
Research on reconstruction of atmospheric turbulence wavefront compressed sensing measurement
-
摘要
压缩感知技术用于大气湍流波前斜率测量能在很大程度上提高波前信号的测量速度，同时降低波前测量系统的硬件压力。与现有波前斜率测量方法不同，压缩感知波前测量方法增加了从波前斜率的稀疏测量值到波前斜率信号的重建过程，因此将压缩感知技术用于波前测量，需要快速、高精度的波前斜率重建算法。Smoothed L0 Norm (SL0)算法是一种近似L0范数估计的优化迭代重建算法，与其它算法相比，不需要事先知道信号的稀疏度，计算量低且估计精度高。本文以SL0算法为基础，对波前斜率信号分区域测量，再结合并行运算，通过理论分析和仿真实验实现了一种能够快速、高精度重建信号的分区域并行算法—Block-Smoothed L0 Norm (B-SL0)。实验结果表明，B-SL0在计算时间和精度都明显优于现有的其它重建算法，对压缩感知技术用于大气湍流波前测量的可行性进行了初步探索。
Abstract
Compressed sensing technology for atmospheric turbulence wavefront slope measurement can greatly improve the wavefront signal measurement speed, while reducing the pressure of wavefront measurement system hardware. Different from the existing wavefront slope measurement method, the compressed sensing wavefront measurement increase a process which from sparse measurement of wavefront slope value to the reconstruction of the wavefront slope signal. Therefore, a fast and accurate wavefront slope reconstruction algorithm is needed if the compressed sensing technology is used for wavefront measurement. Smoothed L0 Norm (SL0) algorithm is an optimized iterative reconstruction algorithm with approximate L0 norm estimation, and compared with other algorithms, it is not necessary to know the sparsity of the signal in advance, and the calculation is low and the estimation accuracy is high. Based on the SL0 algorithm, this paper implements a subregion parallel algorithm-Block-Smoothed L0 Norm (B-SL0) which can quickly and accurately reconstruct the signal by measuring the wavefront slope signal in subarea and parallel operations through theoretical analysis and experiments. The experimental results show that B-SL0 is significantly better than other existing reconstruction algorithms in the calculation time and accuracy, and explore the feasibility of compressed sensing technology for measurement of atmospheric turbulence wavefront preliminarily.
-
Key words:
- compressed sensing /
- wavefront slope /
- SL0 algorithm /
- subregion /
- parallel operation
-
Overview
Overview: Compressed sensing technology for atmospheric turbulence wavefront slope measurement can greatly improve the wavefront signal measurement speed, while reducing the pressure of wavefront measurement system hardware. Different from the existing wavefront slope measurement method, the compressed sensing wavefront measurement increase a process from sparse measurement of wavefront slope value to the reconstruction of the wavefront slope signal, which will increase the wavefront data processing time. So this means putting forward higher demands on the compressed sensing reconstruction algorithm. Therefore, it is necessary to reconstruct wavefront slope quickly and accurately with compressed sensing technology for wavefront measurement.
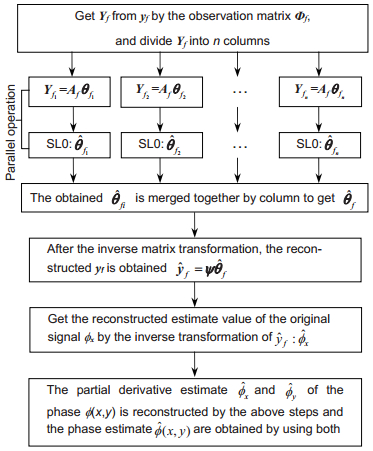
Smoothed L0 Norm (SL0) algorithm is an optimal iterative reconstruction algorithm with approximate L0 norm estimation. Compared with other algorithms, it does not need to know the sparsity of the signal in advance, and it has lower computational complexity and higher estimation accuracy. Because the SL0 algorithm is based on one-dimensional signal reconstruction, while the method of column by line serial reconstruction is used for two-dimensional signals such as wavefront slope. On the one hand, it belongs to serial operation and increases the reconstruction time, on the other hand, it destorys the relationship between the columns of the wavefront slope signal, which reduces the wavefront slope reconstruction precision.
Aiming at the shortcomings of its reconstruction accuracy and running speed, this paper implements a subregion parallel algorithm—Block-Smoothed L0 Norm (B-SL0), which can quickly and accurately reconstruct the signal by measuring the wavefront slope signal in subarea and parallel operations through theoretical analysis and simulation experiments based on the SL0 algorithm the wavefront derivative compressed sensing (DCS). The B-SL0 algorithm uses subregional parallel operation, which not only reduces the running time of the reconstruction algorithm, but also reduces the damage to the internal information of the wavefront slope signal and further improves the reconstruction accuracy of the wavefront phase.
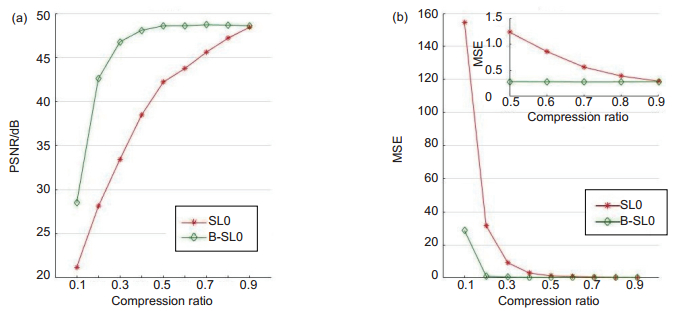
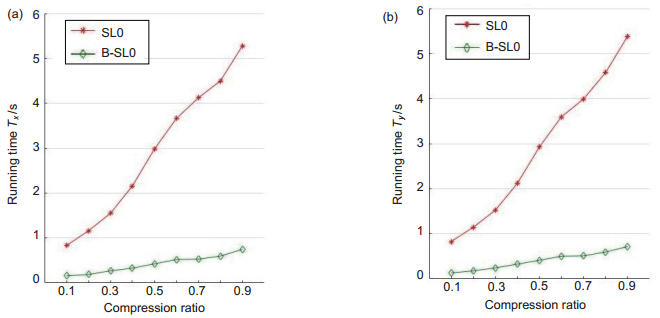
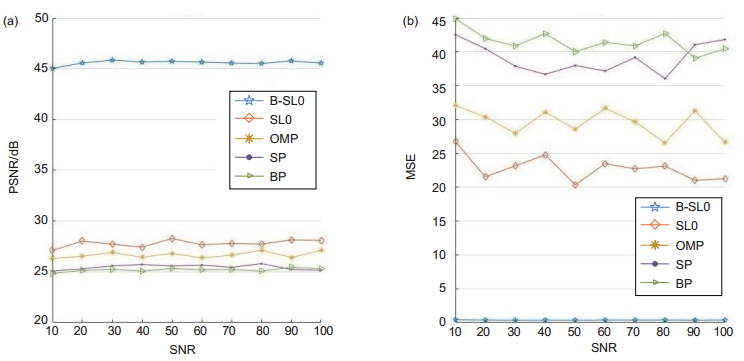
The simulation results show that the B-SL0 algorithm is superior to the SL0 algorithm in terms of the running time of the wavefront slope reconstruction, and the wavefront phase accuracy restored by the reconstructed wavefront slope is better than that of the SL0 algorithm. In addition, compared with some classical algorithms, such as OMP, SP and BP, the B-SL0 algorithm in the same conditions not only greatly improves the running time of the wavefront slope reconstruction, and the reconstructed wavefront slope signal can restore the atmospheric turbulence wavefront phase better, which reflects the performance of the B-SL0 algorithm is good in reconstructing phase screen.
-
-
图 1 波前斜率压缩感知测量过程
Figure 1. The measurement process of wavefront slope compressed sensing
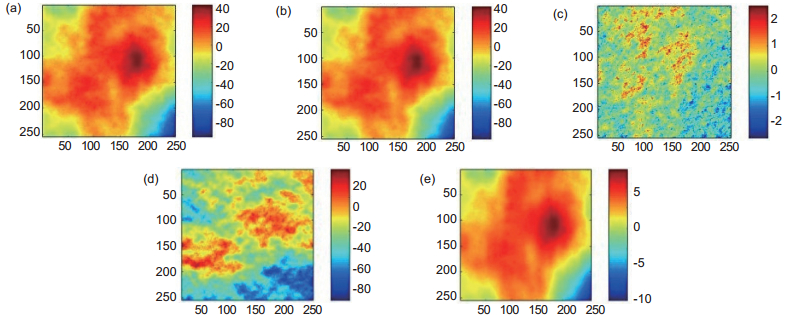
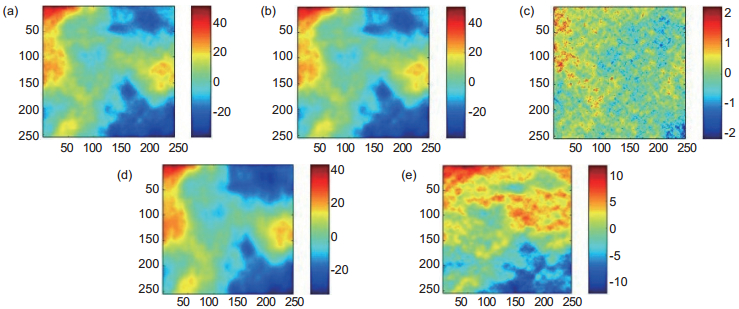
图 4 r=0.3时，B-SL0和SL0重建和重建误差对比图。(a)原图；(b) B-SL0重建图；(c) B-SL0重建误差图；(d) SL0重建图；(e) SL0重建误差图
Figure 4. The reconstruction comparison of B-SL0 and SL0 when r=0.3. (a) Original image; (b) Reconstruction of B-SL0; (c) Reconstruction error of B-SL0; (d) Reconstruction of SL0; (e) Reconstruction error of SL0
图 5 合成相位ϕ峰值信噪比与均方误差分析曲线
Figure 5. The analysis curve about curve peak signal to noise ratio and mean square error of synthetic phase ϕ
图 7 任意一幅相位屏重建对比图。(a)原图；(b) B-SL0重建图；(c) B-SL0重建误差图；(d) SL0重建图；(e) SL0重建误差图
Figure 7. The reconstruction comparison of any one phase screen. (a) Original image; (b) Reconstruction of B-SL0; (c) Reconstruction error of B-SL0; (d) Reconstruction of SL0; (e) Reconstruction error of SL0
图 8 不同信噪比下的PSNR与MSE对比图
Figure 8. Comparison of PSNR and MSE under different signal to noise ratio
表 1 不同相位屏的SL0与B-SL0重建质量对比
Table 1. The reconstruction quality comparison of SL0 and B-SL0 algorithm under different phase screens
Algorithms PSNR/dB MSE Running time/s ϕx ϕy B-SL0 48.48 0.43 0.27 0.24 SL0 35.25 9.70 1.55 1.52 
下载: 导出CSV
表 2 各算法重建质量对比
Table 2. The reconstruction quality comparison of different algorithms
Algorithms PSNR/dB MSE Running time/s ϕx ϕy B-SL0 56.67 0.40 0.26 0.24 SL0 45.09 5.80 1.56 1.54 OMP 44.09 7.30 4.24 4.81 SP 32.73 99.88 1.59 1.59 BP 34.13 72.27 24.26 30.96
下载: 导出CSV
-
参考文献
[1] 林旭东, 薛陈, 刘欣悦, 等.自适应光学波前校正器技术发展现状[J].中国光学, 2012, 5(4): 337–351. http://www.opticsjournal.net/abstract.htm?id=OJ120815000205HdKgMj
Lin X D, Xue C, Liu X Y, et al. Current status and research development of wavefront correctors for adaptive optics[J]. Chinese Optics, 2012, 5(4): 337–351. http://www.opticsjournal.net/abstract.htm?id=OJ120815000205HdKgMj
[2] 鲜浩. 自适应光学系统波前传感器设计与优化[D]. 成都: 电子科技大学, 2008.
Xian H. Design and optimization of wavefront sensor for adaptive optics system[D]. Chengdu: University of Electronic Science and Technology of China, 2008.
[3] 牛超君, 于诗杰, 韩香娥.无波前探测自适应光学对光通信性能影响分析[J].激光与光电子学进展, 2015, 52(8): 080102. http://www.opticsjournal.net/Abstract.htm?id=OJ150723000044bIeKhN
Niu C J, Yu S J, Han X E. Analysis about effect of wavefront sensorless adaptive optics on optical communication[J]. Laser & Optoelectronics Progress, 2015, 52(8): 080102. http://www.opticsjournal.net/Abstract.htm?id=OJ150723000044bIeKhN
[4] 张强, 姜文汉, 许冰.用于Hartmann-Shack波前探测器的区域法算法研究[J].强激光与粒子束, 1998, 10(2): 229–233. http://www.cnki.com.cn/Article/CJFD1998-QJGY802.015.htm
Zhang Q, Jiang W H, Xu B. Study of zonal wavefront reconstruction adapting for Hartmann-Shack wavefront sensor[J]. High Power Laser and Particle Beams, 1998, 10(2): 229–233. http://www.cnki.com.cn/Article/CJFD1998-QJGY802.015.htm
[5] Yazdani R, Fallah H. Wavefront sensing for a Shack–Hartmann sensor using phase retrieval based on a sequence of intensity patterns[J]. Applied Optics, 2017, 56(5): 1358–1364. doi: 10.1364/AO.56.001358
[6] Rostami M, Michailovich O, Wang Z. Image deblurring using derivative compressed sensing for optical imaging application[J]. IEEE Transactions on Image Processing, 2012, 21(7): 3139–3149. doi: 10.1109/TIP.2012.2190610
[7] Polans J, Mcnabb R P, Izatt J A, et al. Compressed wavefront sensing[J]. Optics Letters, 2014, 39(5): 1189–1192. doi: 10.1364/OL.39.001189
[8] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. doi: 10.1109/TIT.2006.871582
[9] 任越美, 张艳宁, 李映.压缩感知及其图像处理应用研究进展与展望[J].自动化学报, 2014, 40(8): 1563–1575. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_zdhxb201408002
Ren Y M, Zhang Y N, Li Y. Advances and perspective on compressed sensing and application on image processing[J]. Acta Automatica Sinia, 2014, 40(8): 1563–1575. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_zdhxb201408002
[10] Tsaig Y, Donoho D L. Extensions of compressed sensing[J]. Signal Processing, 2006, 86(3): 549–571. doi: 10.1016/j.sigpro.2005.05.029
[11] Candès E J, Romberg J, Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489–509. doi: 10.1109/TIT.2005.862083
[12] Candes E J, Tao T. Near-optimal signal recovery from random projections: universal encoding strategies[J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406–5425. doi: 10.1109/TIT.2006.885507
[13] Mallat S G, Zhang Z F. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397–3415. doi: 10.1109/78.258082
[14] Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655–4666. doi: 10.1109/TIT.2007.909108
[15] Yin W, Morgan S, Yang J F, et al. Practical compressive sensing with Toeplitz and circulant matrices[J]. Proceedings of SPIE, 2010, 7744: 77440K. http://cat.inist.fr/?aModele=afficheN&cpsidt=23399639
[16] Applebaum L, Howard S D, Searle S, et al. Chirp sensing codes: Deterministic compressed sensing measurements for fast recovery[J]. Applied & Computational Harmonic Analysis, 2009, 26(2): 283–290. http://www.sciencedirect.com/science/article/pii/S1063520308000869#!
[17] Mohimani H, Babaie-zadeh M, Jutten C. A fast approach for overcomplete sparse decomposition based on smoothed 10 norm[J]. IEEE Transactions on Signal Processing, 2009, 57(1): 289–301. doi: 10.1109/TSP.2008.2007606
[18] Mohimani G H, Babaie-zadeh M, Jutten C. Fast sparse representation based on smoothed l0 norm[C]//Proceedings of the 7th International Conference on Independent Component Analysis and Signal Separation. Springer-Verlag, 2007: 389–396.
[19] Candes, Emmanuel J. The restricted isometry property and its implications for compressed sensing[J]. Comptes rendus-Mathematique, 2008, 346(9): 589–592. https://www.sciencedirect.com/science/article/pii/S1631073X08000964
[20] Cai T T, Wang L, Xu G W. New bounds for restricted isometry constants[J]. IEEE Transactions on Information Theory, 2010, 56(9): 4388–4394. doi: 10.1109/TIT.2010.2054730
[21] 蔡冬梅, 王昆, 贾鹏, 等.功率谱反演大气湍流随机相位屏采样方法的研究.物理学报, 2014, 63(10): 104217. doi: 10.7498/aps.63.104217
Cai D M, Wang K, Jia P, et al. Sampling methods of power spectral density method simulating atmospheric turbulence phase screen[J]. Journal of physics, 2014, 63(10): 104217. doi: 10.7498/aps.63.104217
[22] 张智露. 室内大气湍流模拟系统的研究[D]. 太原: 太原理工大学, 2017.
Zhang Z L. Research on the simulation system of indoor atmospheric turbulence[D]. Taiyuan: Taiyuan University of Technology, 2017.
[23] 李玉杰, 朱文越, 饶瑞中.非Kolmogorov大气湍流随机相位屏模拟[J].红外与激光工程, 2016, 45(12): 1211001. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=hwyj201612029&dbname=CJFD&dbcode=CJFQ
Li Y J, Zhu W Y, Rao R Z. Simulation of random phase screen of non-Kolmogorov atmospheric turbulence[J]. Infrared and Laser Engineering, 2016, 45(12): 1211001. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=hwyj201612029&dbname=CJFD&dbcode=CJFQ
-
访问统计
点击扫一扫
图(8)
表(2)
计量
- 文章访问数:
- PDF下载数:
- 施引文献: 0
