-
摘要:
轨道角动量(OAM)光束具有螺旋形相位分布,在信息光学、光捕获、光学操控等领域都有着重要的应用。本文设计了一种可以生成聚焦OAM光束的平面型光学器件。该器件利用迂回相位的编码方式,在平板上加载了根据分数Talbot效应计算得到的特定相位分布。使用时域有限差分(FDTD)分别对具有正方形和六边形周期性结构的光学器件进行仿真模拟。结果表明,平面波经过此器件可以转化为阵列型聚焦OAM光束。该器件加工方便,容易拼接或复制,集成度高,可以用来生成高质量大面积阵列型OAM光束。

-
关键词:
- 分数Talbot效应 /
- 轨道角动量 /
- 周期性结构 /
- 迂回相位
Abstract:Orbital angular momentum (OAM) beam with helical phase distribution has demonstrated important applications in information optics, optical trapping, and optical manipulation. In this paper, we designed a planar optical device which can generate a periodic array of focused orbital angular momentum beams. Based on detour phase encoding, the phase distribution calculated by fractional Talbot effect is implemented on this planar optical device. The property of this optical device with periodic square and hexagonal structures is simulated by finite difference time domain (FDTD) respectively. The optical device with explicit advantages of being easy to fabricate, splice, duplicate, and integrate can efficiently prop up the generation of high-quality large-area array-type OAM beams.
-
Key words:
- fractional Talbot effect /
- orbital angular momentum /
- periodic structure /
- detour phase
-

Overview: Orbital angular momentum (OAM) beam with helical phase distribution has demonstrated important applications in information optics, optical storage, laser processing, super-resolution, optical trapping, and optical manipulation. These exceptional achievements heavily rely on the development of OAM micro-devices that can precisely manipulate optical fields of demand. As such functional components gradually reach out to large-scale production for practical applications from the laboratory-scale researches, more requirements are raised for producing OAM beams with equal properties in batches. At present, there are varied methods to generate OAM beams, for example, spiral phase plate method, variable spiral plate method, hologram folk grating method, and spatial light modulator method. However, the above methods are mostly focused on generating a single OAM beam, which overlooks the needs of fostering multi-focus array light field that is highly desirable for novel functions in numerous studies. How to readily realize focused OAM arrays beams over a large area remains a tough challenge from concept to implementation. In this paper, based on fractional Talbot effect, we have designed a planar optical device which can generate periodic array of focused orbital angular momentum beam. The phase distribution of the devised structure contains two parts: the focusing lens phase distribution and the spiral vortex phase distribution. According to detour phase encoding, the phase distribution calculated by fractional Talbot effect is implemented on the planar optical device by discretizing the phase distribution with arrayed phase-control units. The multi-level phase distribution is transformed to the lateral displacement of the rectangular bars from the center of each unit cell, which is proportioned to the phase shift as designed. The focusing property of this optical device with periodic square and hexagonal structures are simulated by finite difference time domain (FDTD). The intensity distribution and phase profile of each single focused light beam in the illumination plane are virtually identical. With changing the arrangement of the phase-regulation unit from square to hexagonal Talbot array, the symmetry of the intensity distribution for the focused light spot with vortex phase distribution changes accordingly. The symmetry of the hexagonal Talbot array is higher than the square counterpart. This optical device with explicit advantages of being easy to fabricate, splice, duplicate, and integrate can efficiently prop up the generation of high-quality large-area array-type OAM beams for widely spreading applications in optical trapping, optical manipulation, optical fabrication, and other fields.
-

-
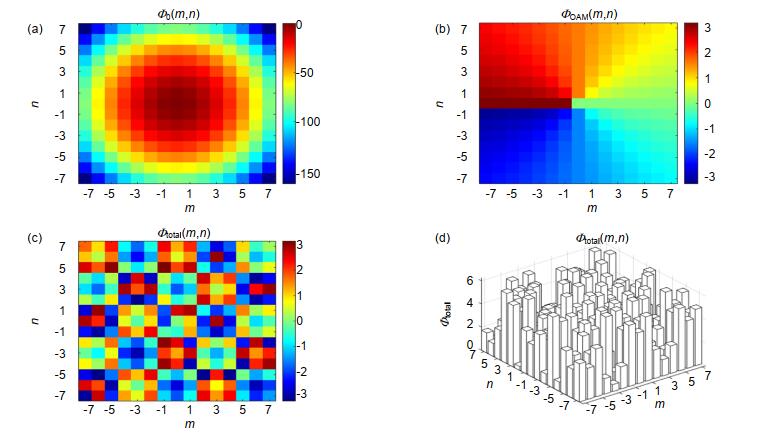
图 1 (a), (b)正方形单周期Talbot相位板的(a)相位分布和(b) l = 1的螺旋相位分布;(c), (d)叠加轨道角动量的Talbot相位板的(c)总相位分布和其相应的(d)三维立体结构。
Figure 1. (a), (b) Single period of square Talbot phase plate phase distribution (a) and helical phase distribution for l = 1 (b); (c), (d) The total phase distribution (c) of Talbot phase distribution with orbital angular momentum and its three dimensional structure (d)
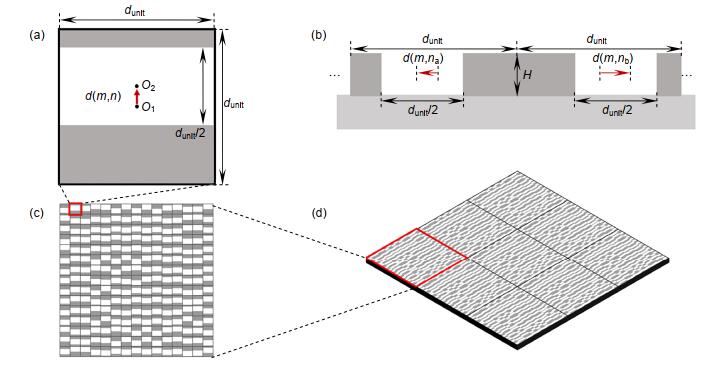
图 2 (a), (b)迂回相位编码Talbot阵列照明器的正方形1×1像素(a)基元结构(其中d(m, n)为0相位中心位置偏移量,O1和O2分别对应基元中心和0相位中心)和(b)位置偏移;(c), (d)迂回相位编码Talbot阵列照明器的(c)单周期和(d)3×3周期阵列结构
Figure 2. (a), (b) The square unit cell (a) of Talbot array illuminator based on detour phase encoding and its displacement (b) from the central position; (c), (d) One period (c) and 3×3 array structures (d) of Talbot array illuminator based on detour phase encoding
图 3 (a), (b)迂回相位编码的正方形Talbot阵列照明器的(a) l=0和(b) l=+1的电场强度分布;(c), (d)分别是l=0和l=+1的FDTD模拟仿真计算结果;(e) l=+1的阵列型电场强度分布
Figure 3. (a), (b) Electric field intensity distribution of (a) l=0 and (b) l=+1 for square Talbot array illuminator based on detour phase encoding; (c), (d) The corresponding simulated results are shown in (c) and (d); (e) Electric field intensity distribution ofl=+1 for 5×5 Talbot array illuminator
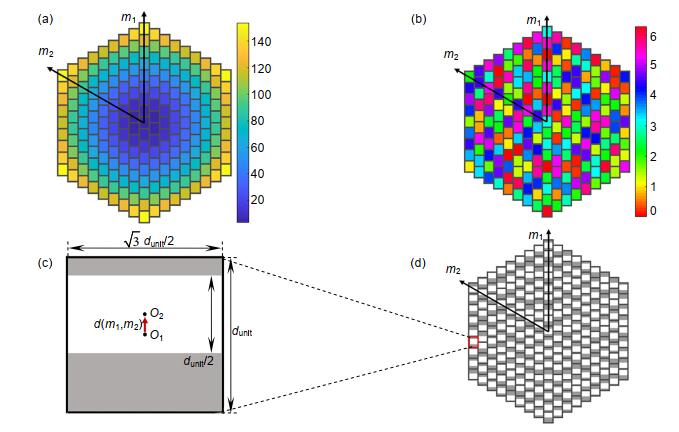
图 4 (a) 六边形单周期Talbot相位板的相位分布;(b) l=+1的螺旋相位分布;(c)迂回相位编码六边形Talbot阵列照明器的1×1像素基元结构;(d)迂回相位编码的六边形Talbot阵列照明器
Figure 4. (a) One period of hexagonal Talbot phase plate phase distribution; (b) Helical phase distribution for l=1; (c), (d) The unit cell (c) and one period of hexagonal (d) Talbot array illuminator based on detour phase encoding
图 5 (a)~(d)迂回相位编码的六边形Talbot阵列照明器的(a) l=0, (b) l=+1, (c) l=-1和(d) l=+2的归一化电场强度分布;(e) l=+1的阵列型电场强度分布
Figure 5. (a)~(d) Normalized electric field intensity distribution of (a) l=0, (b) l=+1, (c) l=-1, and (d) l=+2 for hexagonal Talbot array illuminator based on detour phase encoding respectively; (e) Electric field intensity distribution of l=+1 for Talbot array illuminator
-
[1] Allen L, Beijersbergen M W, Spreeuw R J C, et al. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes[J]. Physical Review A, 1992, 45(11): 8185-8189. doi: 10.1103/PhysRevA.45.8185
[2] Wang J, Yang J Y, Fazal I M, et al. Terabit free-space data transmission employing orbital angular momentum multiplexing[J]. Nature Photonics, 2012, 6(7): 488-496. doi: 10.1038/nphoton.2012.138
[3] Bozinovic N, Yue Y, Ren Y X, et al. Terabit-scale orbital angular momentum mode division multiplexing in fibers[J]. Science, 2013, 340(6140): 1545-1548. doi: 10.1126/science.1237861
[4] Vallone G, D'Ambrosio V, Sponselli A, et al. Free-space quantum key distribution by rotation-invariant twisted photons[J]. Physical Review Letters, 2014, 113(6): 060503. doi: 10.1103/PhysRevLett.113.060503
[5] Gan Z S, Cao Y Y, Evans R A, et al. Three-dimensional deep sub-diffraction optical beam lithography with 9 nm feature size[J]. Nature Communications, 2013, 4: 2061. doi: 10.1038/ncomms3061
[6] 曹耀宇, 谢飞, 张鹏达, 等.双光束超分辨激光直写纳米加工技术[J].光电工程, 2017, 44(12): 1133-1145. doi: 10.3969/j.issn.1003-501X.2017.12.001
Cao Y Y, Xie F, Zhang P D, et al. Dual-beam super-resolution direct laser writing nanofabrication technology[J]. Opto-Electronic Engineering, 2017, 44(12): 1133-1145. doi: 10.3969/j.issn.1003-501X.2017.12.001
[7] Lehmuskero A, Li Y M, Johansson P, et al. Plasmonic particles set into fast orbital motion by an optical vortex beam[J]. Optics Express, 2014, 22(4): 4349-4356. doi: 10.1364/OE.22.004349
[8] Grier D G. A revolution in optical manipulation[J]. Nature, 2003, 424(6950): 810-816. doi: 10.1038/nature01935
[9] Tao S H, Yuan X C, Lin J, et al. Fractional optical vortex beam induced rotation of particles[J]. Optics Express, 2005, 13(20): 7726-7731. doi: 10.1364/OPEX.13.007726
[10] Ladavac K, Grier D G. Microoptomechanical pumps assembled and driven by holographic optical vortex arrays[J]. Optics Express, 2004, 12(6): 1144-1149. doi: 10.1364/OPEX.12.001144
[11] Ni J C, Wang C W, Zhang C C, et al. Three-dimensional chiral microstructures fabricated by structured optical vortices in isotropic material[J]. Light: Science & Applications, 2017, 6(7): e17011. https://arxiv.org/pdf/1608.01220.pdf
[12] Ouyang X, Xu Y, Feng Z W, et al. Polychromatic and polarized multilevel optical data storage[J]. Nanoscale, 2019, 11(5): 2447-2452. doi: 10.1039/C8NR09192G
[13] Li X P, Cao Y Y, Tian N, et al. Multifocal optical nanoscopy for big data recording at 30 TB capacity and gigabits/second data rate[J]. Optica, 2015, 2(6): 567-570. doi: 10.1364/OPTICA.2.000567
[14] 欧阳旭, 徐毅, 冼铭聪, 等.基于无序金纳米棒编码的多维光信息存储[J].光电工程, 2019, 46(3): 180584. doi: 10.12086/oee.2019.180584
Ouyang X, Xu Y, Xian M C, et al. Encoding disorder gold nanorods for multi-dimensional optical data storage[J]. Opto-Electronic Engineering, 2019, 46(3): 180584. doi: 10.12086/oee.2019.180584
[15] 姜美玲, 张明偲, 李向平, 等.超分辨光存储研究进展[J].光电工程, 2019, 46(3): 180649. doi: 10.12086/oee.2019.180649
Jiang M L, Zhang M S, Li X P, et al. Research progress of super-resolution optical data storage[J]. Opto-Electronic Engineering, 2019, 46(3): 180649. doi: 10.12086/oee.2019.180649
[16] Campbell G, Hage B, Buchler B, et al. Generation of high-order optical vortices using directly machined spiral phase mirrors[J]. Applied Optics, 2012, 51(7): 873-876. doi: 10.1364/AO.51.000873
[17] Wei D Z, Wu Y, Wang Y M, et al. Survival of the orbital angular momentum of light through an extraordinary optical transmission process in the paraxial approximation[J]. Optics Express, 2016, 24(11): 12007-12012. doi: 10.1364/OE.24.012007
[18] Beresna M, Gecevičius M, Kazansky P G, et al. Radially polarized optical vortex converter created by femtosecond laser nanostructuring of glass[J]. Applied Physics Letters, 2011, 98(20): 201101. doi: 10.1063/1.3590716
[19] Nersisyan S R, Tabiryan N V, Mawet D, et al. Improving vector vortex waveplates for high-contrast coronagraphy[J]. Optics Express, 2013, 21(7): 8205-8213. doi: 10.1364/OE.21.008205
[20] Marrucci L, Manzo C, Paparo D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media[J]. Physical Review Letters, 2006, 96(16): 163905. doi: 10.1103/PhysRevLett.96.163905
[21] Mair A, Vaziri A, Weihs G, et al. Entanglement of the orbital angular momentum states of photons[J]. Nature, 2001, 412(6844): 313-316. doi: 10.1038/35085529
[22] Wei B Y, Hu W, Ming Y, et al. Generating switchable and reconfigurable optical vortices via photopatterning of liquid crystals[J]. Advanced Materials, 2014, 26(10): 1590-1595. doi: 10.1002/adma.201305198
[23] Wang X L, Lou K, Chen J, et al. Unveiling locally linearly polarized vector fields with broken axial symmetry[J]. Physical Review A, 2011, 83(6): 063813. doi: 10.1103/PhysRevA.83.063813
[24] Wang X L, Chen J, Li Y N, et al. Optical orbital angular momentum from the curl of polarization[J]. Physical Review Letters, 2010, 105(25): 253602. doi: 10.1103/PhysRevLett.105.253602
[25] Wang X L, Li Y N, Chen J, et al. A new type of vector fields with hybrid states of polarization[J]. Optics Express, 2010, 18(10): 10786-10795. doi: 10.1364/OE.18.010786
[26] Cai X L, Wang J W, Strain M J, et al. Integrated compact optical vortex beam emitters[J]. Science, 2012, 338(6105): 363-366. doi: 10.1126/science.1226528
[27] Yu N F, Capasso F. Flat optics with designer metasurfaces[J]. Nature Materials, 2014, 13(2): 139-150. doi: 10.1038/nmat3839
[28] Karimi E, Schulz S A, de Leon I, et al. Generating optical orbital angular momentum at visible wavelengths using a plasmonic metasurface[J]. Light: Science & Applications, 2014, 3(5): e167. https://www.nature.com/articles/lsa201448
[29] Talbot H F. LXXVI. Facts relating to optical science. No. Ⅳ[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1836, 9(56): 401-407. doi: 10.1080/14786443608649032
[30] Rayleigh L. XXV. On copying diffraction-gratings, and on some phenomena connected therewith[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1881, 11(67): 196-205. doi: 10.1080/14786448108626995
[31] Zhu L W, Yin X, Hong Z P, et al. Reciprocal vector theory for diffractive self-imaging[J]. Journal of the Optical Society of America A, 2008, 25(1): 203-210. doi: 10.1364/JOSAA.25.000203
[32] Li Z G, Yang R, Sun M Y, et al. Detour phase Talbot array illuminator[J]. Chinese Optics Letters, 2019, 17(7): 070501. doi: 10.3788/COL201917.070501
[33] Brown B R, Lohmann A W. Complex spatial filtering with binary masks[J]. Applied Optics, 1966, 5(6): 967-969. doi: 10.1364/AO.5.000967
[34] Lohmann A W, Paris D P. Binary fraunhofer holograms, generated by computer[J]. Applied Optics, 1967, 6(10): 1739-1748. doi: 10.1364/AO.6.001739
-


 E-mail Alert
E-mail Alert RSS
RSS
 下载:
下载: